反射
- 次の図において四角形\(ABCD\)は長方形であり、
- \(AB=12cm\)、\(BC=15cm\)、\(BE=10cm\)のとき、\(AE+EF+FG\)の長さを求めなさい。
- \(A\)から出た光は長方形\(ABCD\)の辺にくるたびに反射を繰り返し、頂点のいずれかにくるまで進む。\(AB=8cm\)、\(BC=15cm\)、\(BE=12cm\)のとき、光の進んだ距離を求めなさい。
\(A\)から出された光は反射しながら\(E→F→G・・・\)と進む。
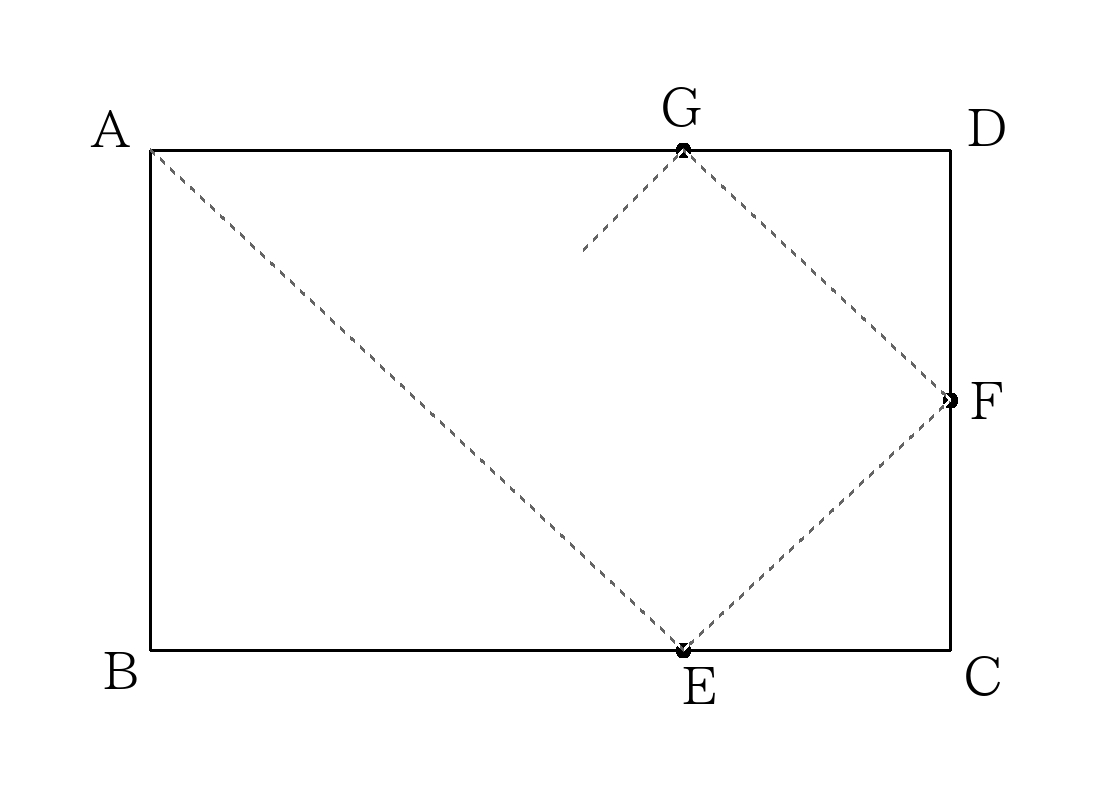
- 対称な図形を書き加えながら解く!
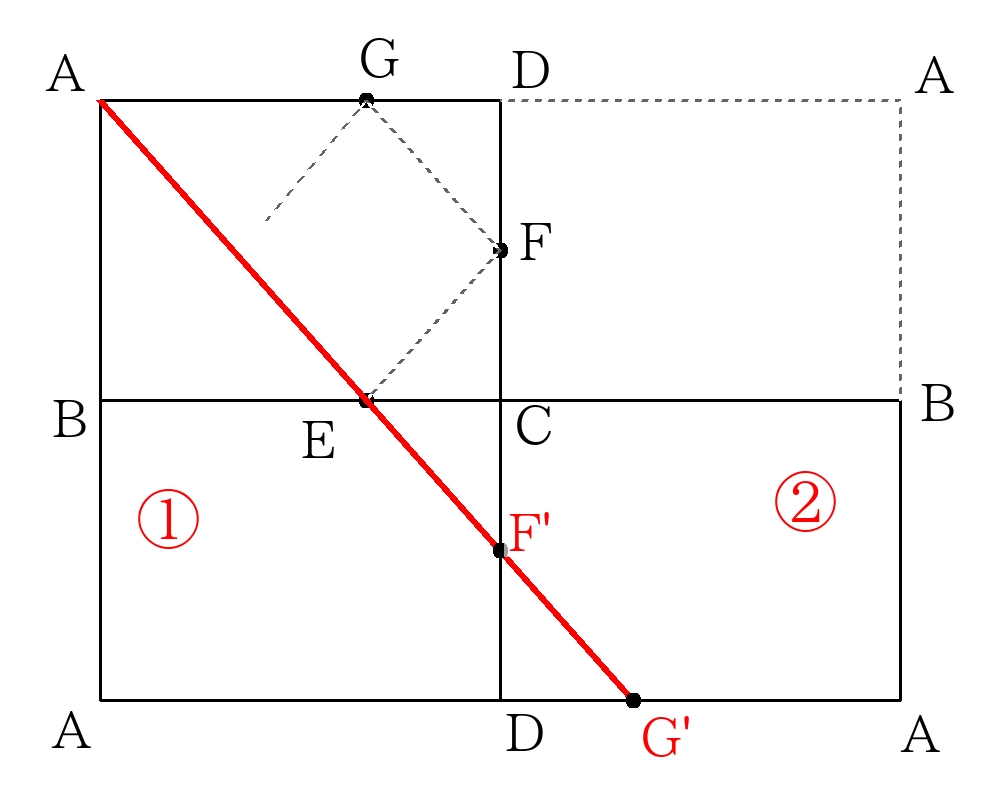
まず、辺\(BC\)で反射するので、\(BC\)に対称な図形( \( \color{red}{①} \) )を書く。
直線\(AE\)と\( \color{red}{①} \)の\(CD\)との交点を\(F’\)とする。
このとき、\(EF=EF’\)であることを確認。
次に辺\(CD\)で反射するので、\(CD\)に対称な図形( \( \color{red}{②} \) )を書く。
直線\(AE\)と\( \color{red}{②} \)の\(DA\)との交点を\(G’\)とする。
このとき、\(FG=F’G’\)であることを確認。
・・・以下同様の操作を繰り返す。
すると、はじめに折れ線で表されていた光の道すじを直線で表すことができる。
入射角と反射角が等しいことと三角形の合同からこれらの解法が正しいことは説明できる。
- 次の図において四角形\(ABCD\)は長方形であり、
- \(AB=12cm\)、\(BC=15cm\)、\(BE=10cm\)のとき、\(AE+EF+FG\)の長さを求めなさい。
- \(A\)から出た光は長方形\(ABCD\)の辺にくるたびに反射を繰り返し、頂点のいずれかにくるまで進む。\(AB=8cm\)、\(BC=15cm\)、\(BE=12cm\)のとき、光の進んだ距離を求めなさい。
\(A\)から出された光は反射しながら\(E→F→G・・・\)と進む。

作図する。
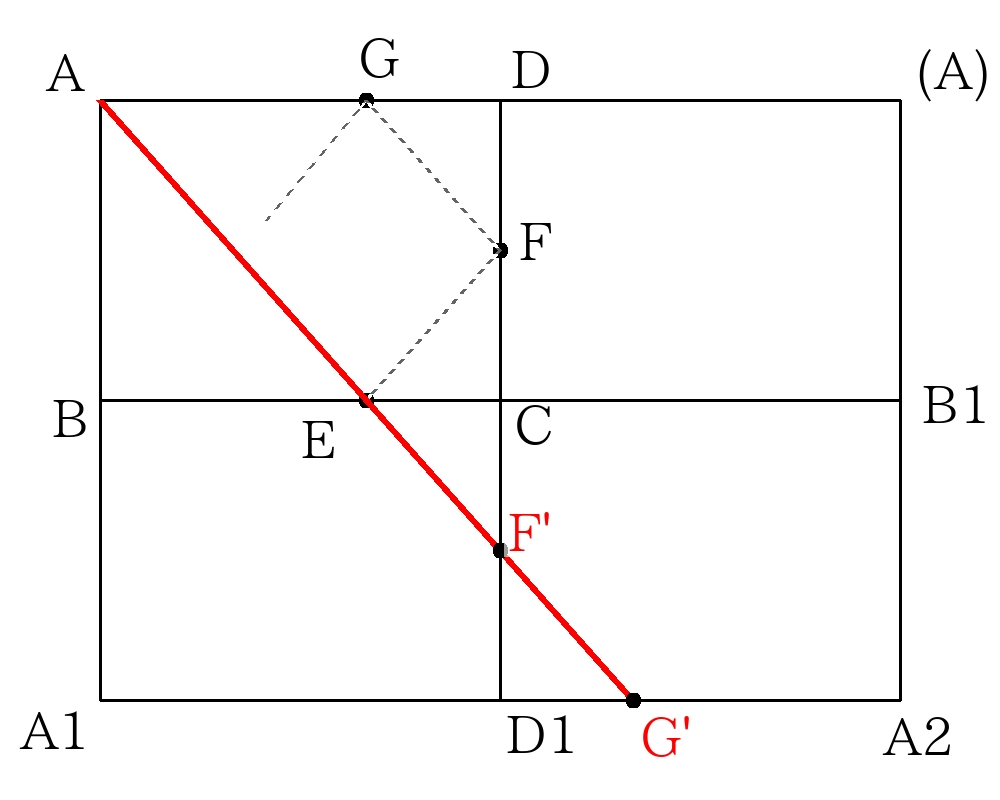
\(AE+EF+FG=AG’\)は直角三角形\(AA_{1}G’\)から求めれば良い。
\(AA1=AB \times 2=24 cm \)
\( \triangle ABE \)∽\( \triangle AA1G’ \)であり、\(AB:AA1=1:2\)より
\(A1G’=BE \times 2 =20 cm\)
\( AG’=\sqrt{ 24^2 + 20^2 }=4 \sqrt{61} \)
\(4 \sqrt{61}cm\)
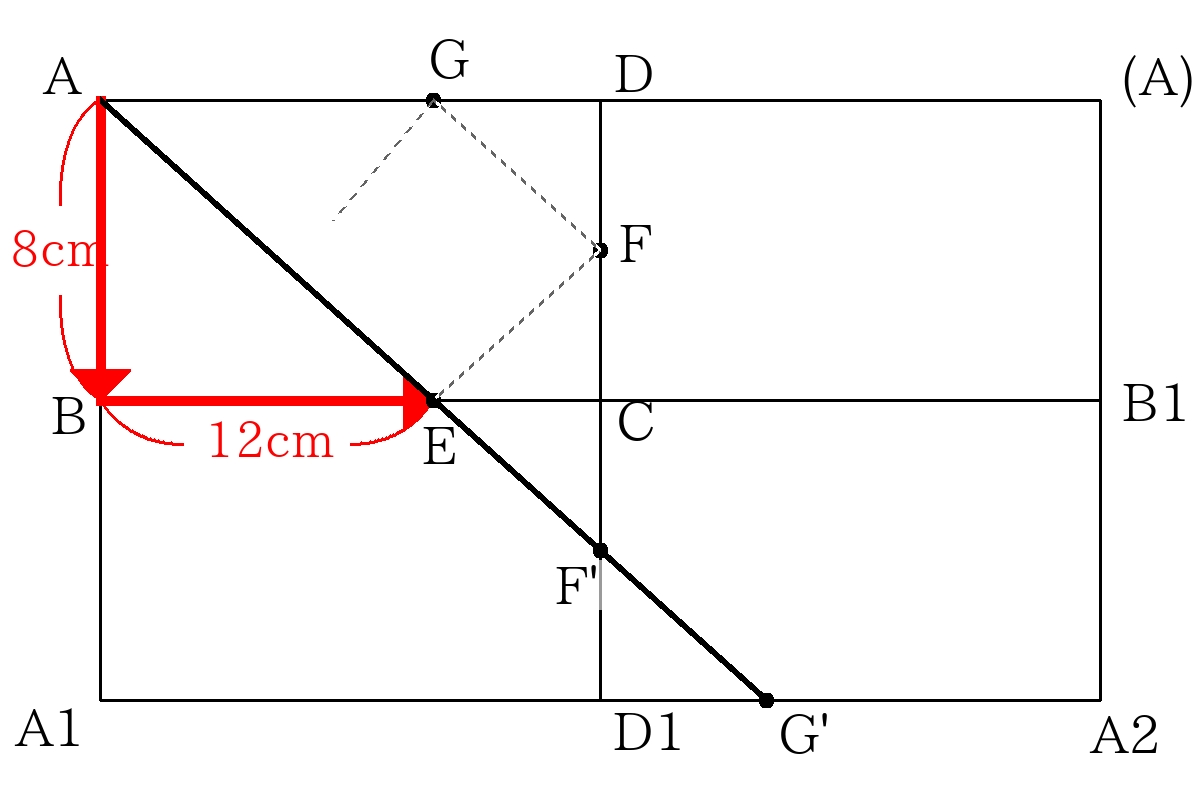
図より、光は(たて)\(:\)(横)\(=8:12=2:3\)の比で進む。
長方形をたてに\(n\)枚、横に\(m\)枚並べたときに光が頂点に来るとすると、
光が進んだ長さは、たてに\(8n _{(cm)}\)、横に\(15m _{(cm)}\)であり、この比が\(2:3\)になれば良いので、
\(8n:15m=2:3\)
\(24n=30m\)
\(4n=5m\)
\(n:m=5:4\)
よって縦に5枚、横に4枚長方形を並べたときに頂点に来ることがわかる。
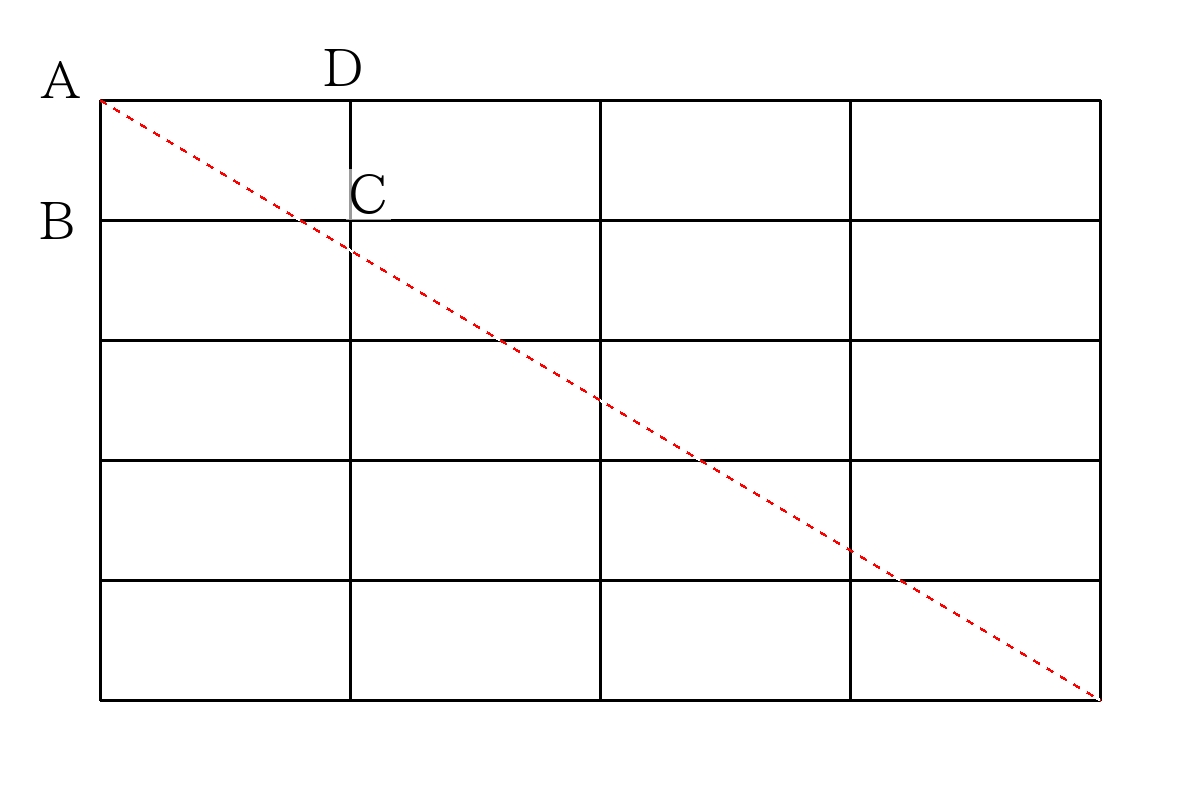
よって光の進んだ距離は、縦にたてに\(40cm\)、横に\(60cm\)進んだときの斜辺なので、
\( \sqrt{40^2+60^2} = 20 \sqrt{13} \)
\(20 \sqrt{13}cm\)



コメント