等積変形
放物線\(m:y=x^2\)と直線①があり、点\(A\)、\(B\)で交わっている。\(A\)、\(B\)の\(x\)座標がそれぞれ\(-2\)、\(4\)のとき次の問に答えなさい。
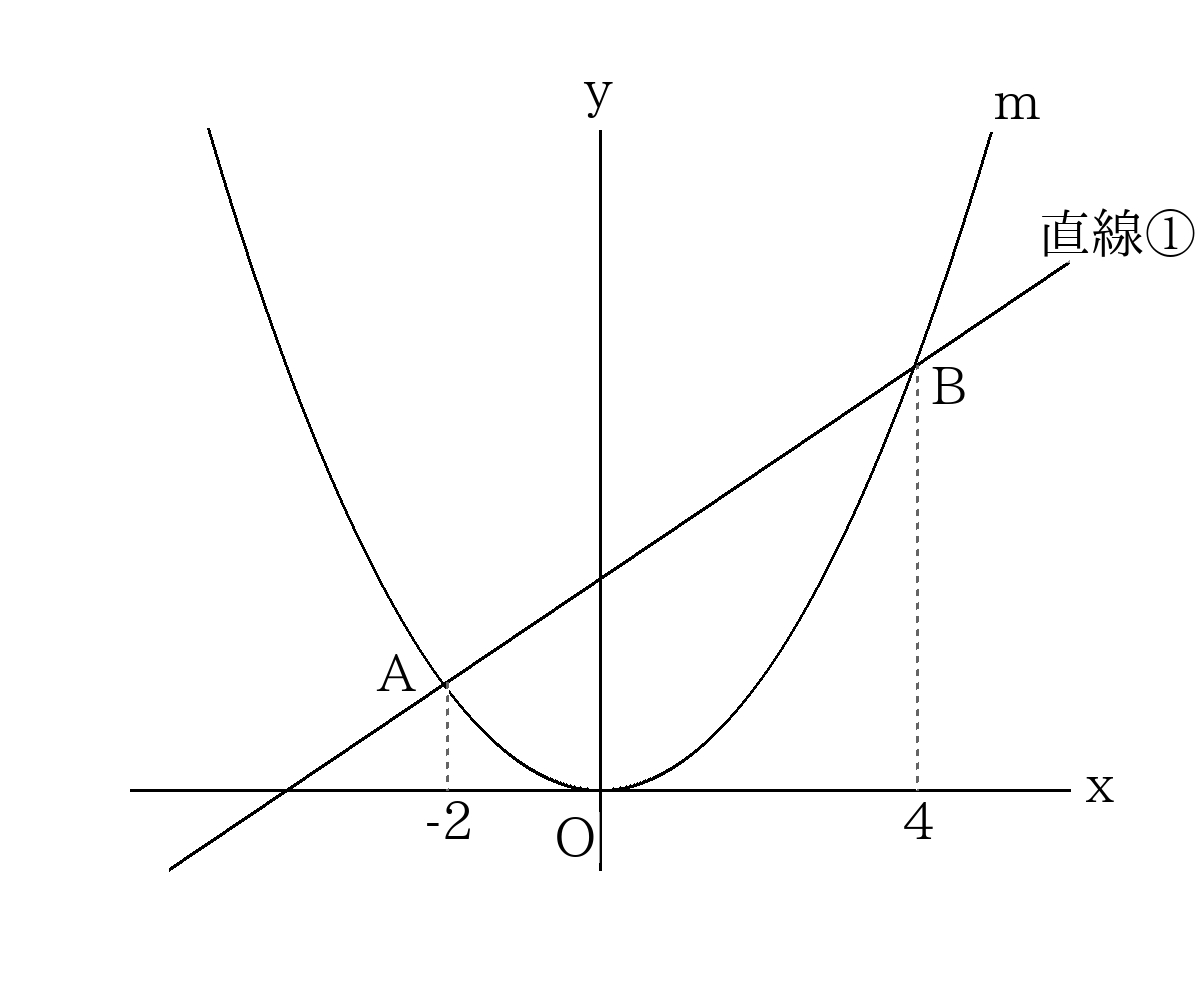
- 直線①の式を求めなさい。
- 放物線\(m\)上に点\(P\)を取り、\( \triangle ABO= \triangle ABP \)となるようにしたい。このとき点\(P\)の\(x\)座標として考えられるものをすべて答えなさい。
- \(y\)軸上に点\(Q\)を取り、\( \triangle ABQ= 2 \triangle ABO \) (\( \triangle ABQ \)の面積が \( \triangle ABO \)の面積の2倍) となるようにしたい。このとき点\(Q\)の\(y\)座標として考えられるものをすべて答えなさい。
- 面積が等しい→平行な線で挟み込め!
【等積変形の基本原理】
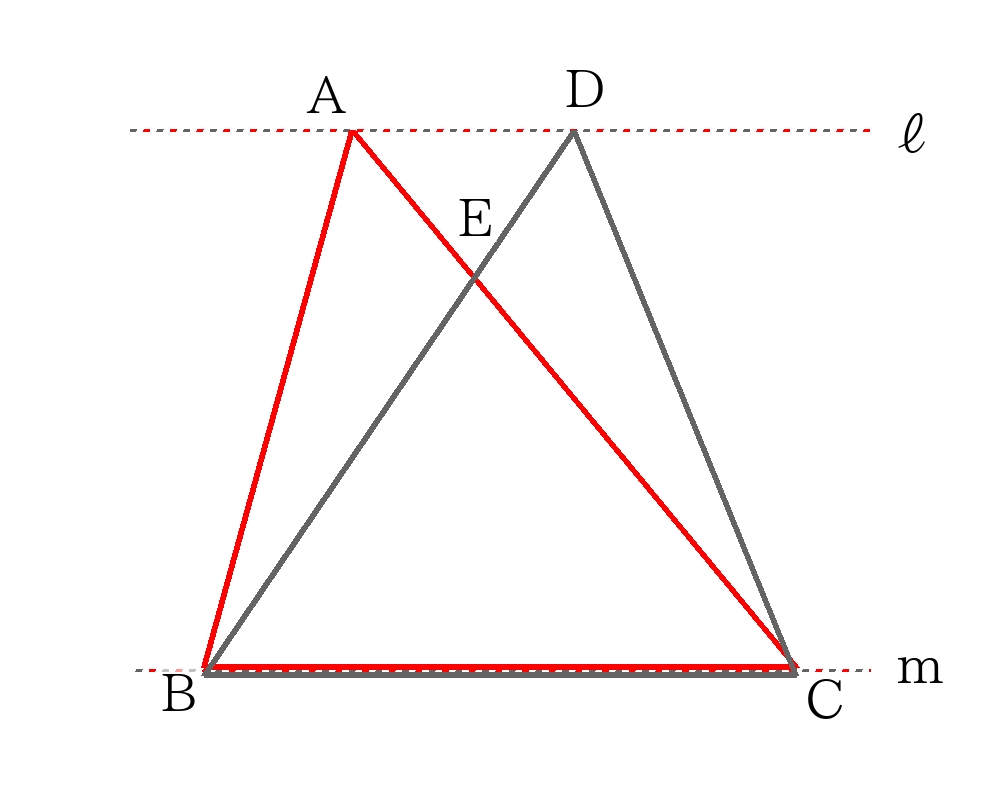
\(ℓ /\!/ m\)のとき、\( \triangle ABC = \triangle DCB \)、\( \triangle ABE = \triangle DCE \)
- 放物線\(m:y=x^2\)と直線①があり、点\(A\)、\(B\)で交わっている。\(A\)、\(B\)の\(x\)座標がそれぞれ\(-2\)、\(4\)のとき次の問に答えなさい。
- 直線①の式を求めなさい。
- 放物線\(m\)上に点\(P\)を取り、\( \triangle ABO= \triangle ABP \)となるようにしたい。このとき点\(P\)の\(x\)座標として考えられるものをすべて答えなさい。
- \(y\)軸上に点\(Q\)を取り、\( \triangle ABQ= 2 \triangle ABO \) (\( \triangle ABQ \)の面積が \( \triangle ABO \)の面積の2倍) となるようにしたい。このとき点\(Q\)の\(y\)座標として考えられるものをすべて答えなさい。

放物線と直線の交点の公式より
\(y=1(-2+4)x-(-2) \times 4 \)
\(y=2x+8 \)
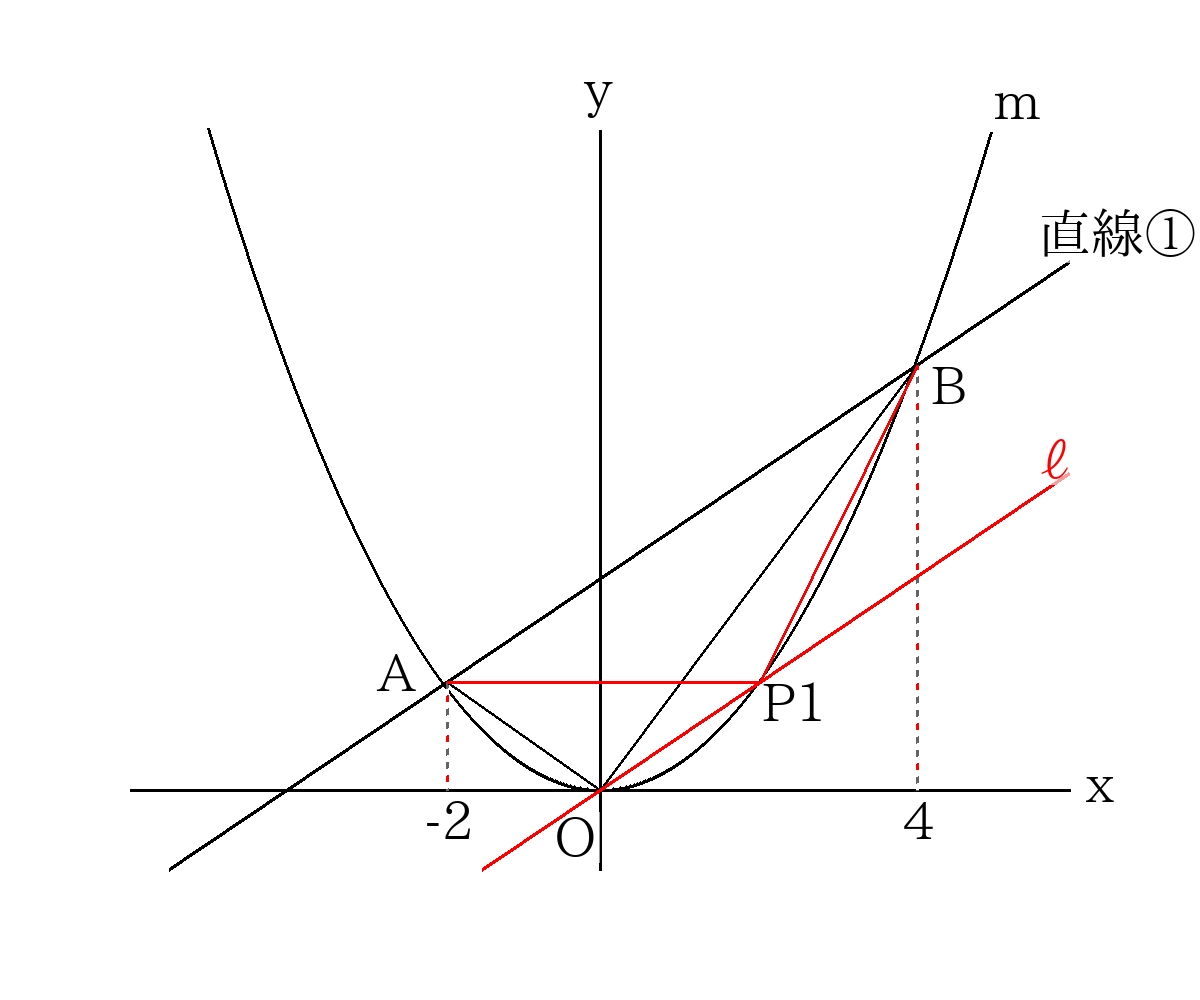
\( \triangle ABO\)と\(\triangle ABP \)は底辺\(AB\)が共通なので、高さが等しければ良い。
\(O\)を通り\(AB\)に平行な直線\(ℓ\)を引き、直線\(ℓ\)と放物線との交点を\(P_{1}\)とする。
このとき、\( \triangle ABO= \triangle ABP_{1} \)なので、\(P_{1}\)は\(P\)としての条件を満たす。
\(y=2x\)と\(y=x^2\)の交点を求めれば良いので、\(P_{1}\)の\(x\)座標は\(x=2\)
さらに\( \triangle ABP \)の頂点\(P\)は原点\(O\)と反対側にも取ることができる。
直線\(AB\)と直線\(ℓ\)の\(y\)切片の差と同じになるよう、反対側にも平行な直線\(n\)を引く。
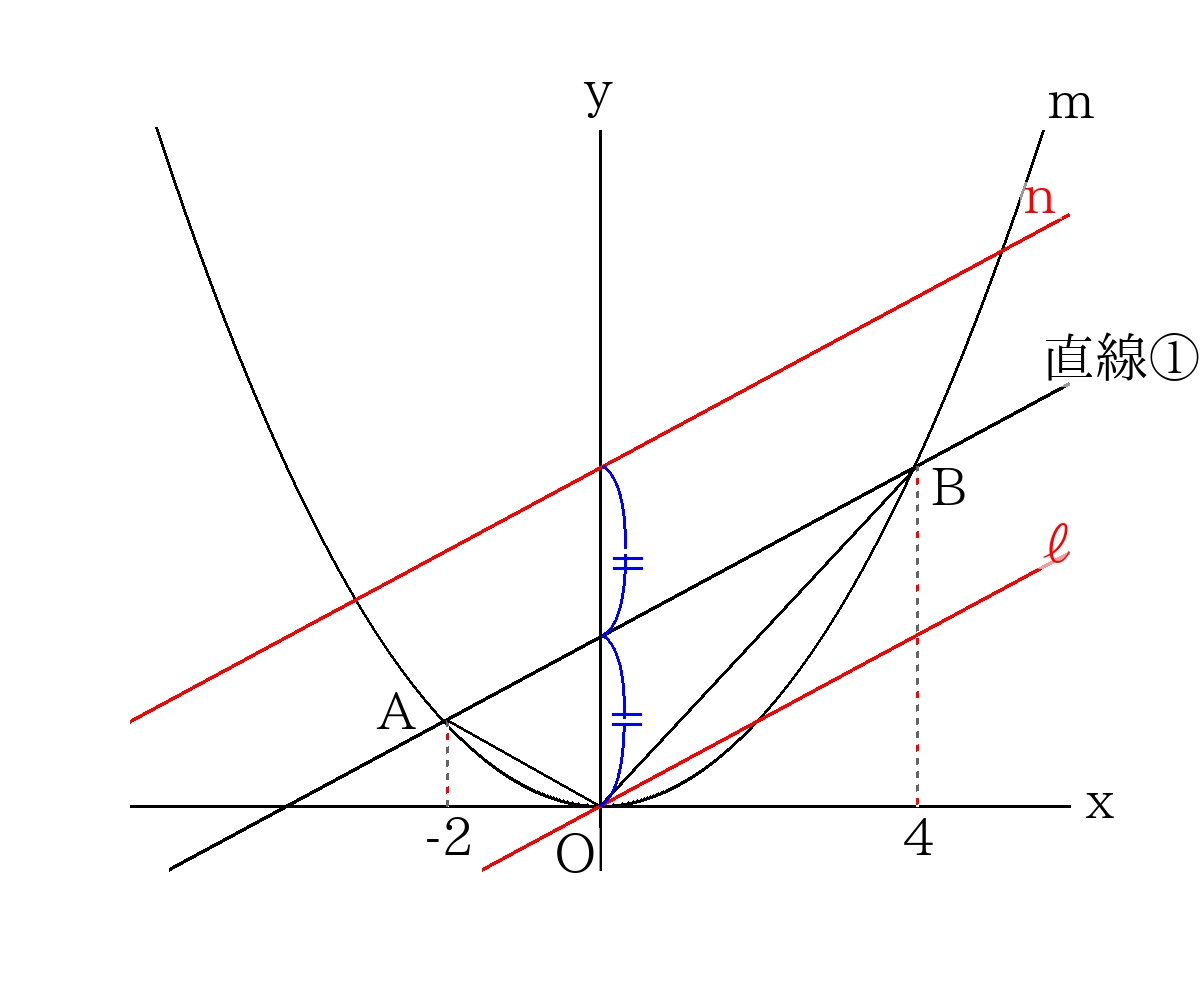
さらに直線\(n\)と放物線との交点を\(P_2\)、\(P_3\)とする。
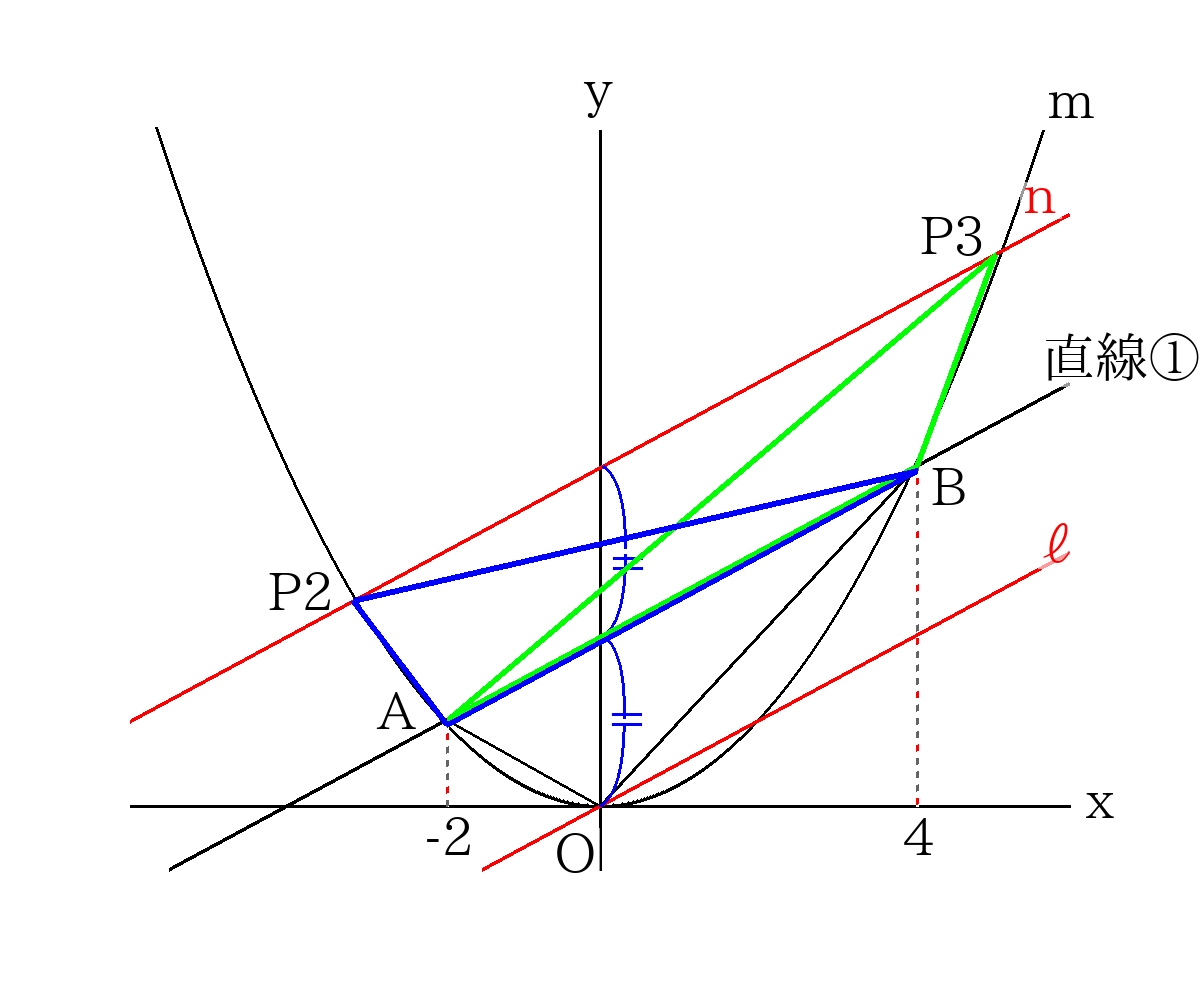
このとき、\(\triangle ABP_2\)、\(\triangle ABP_3\)は\(\triangle ABO\)の面積と等しいので、\(P_2\)、\(P_3\)は点\(P\)としての条件を満たす。
直線\(n\)の式は\(y=2x+16\)なので\(P_2\)、\(P_3\)の\(x\)座標を求めると、
\(x=1±\sqrt{17}\)
よって、求めるべき点\(P\)の\(x\)座標は、\(P_1\)、\(P_2\)、\(P_3\)の\(x\)座標なので
\(x=2,1± \sqrt{17} \)
②の問題のように\(y\)切片との差により面積が決まる。
今回は面積が2倍なので、\(y\)切片との差が2倍になるような位置に点を取れば良い。
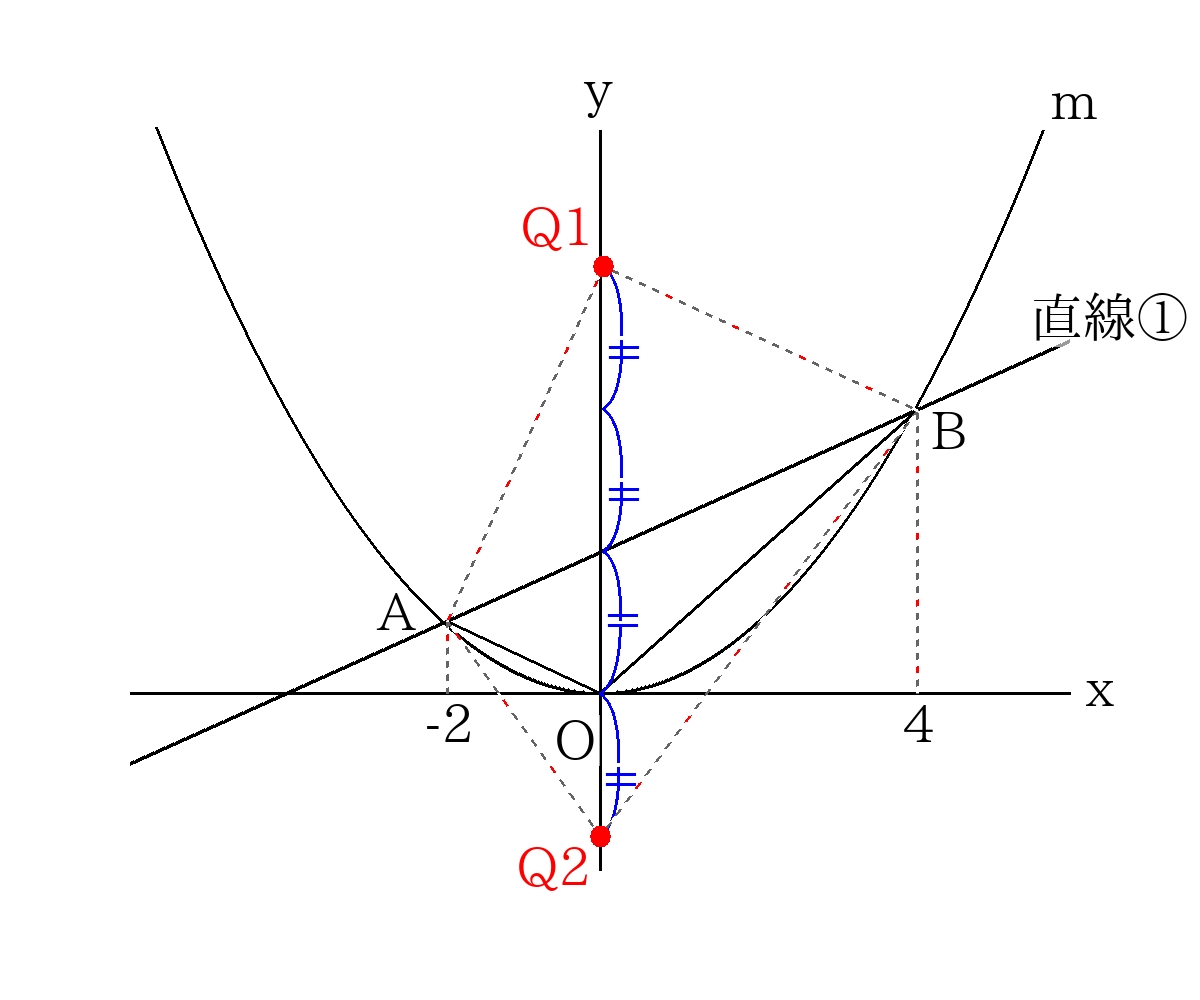
直線\(AB\)の切片が\(8\)なので、\(Q_1\)、\(Q_2\)の\(y\)座標は
\(y=-8,24 \)



コメント