媒介変数と軌跡
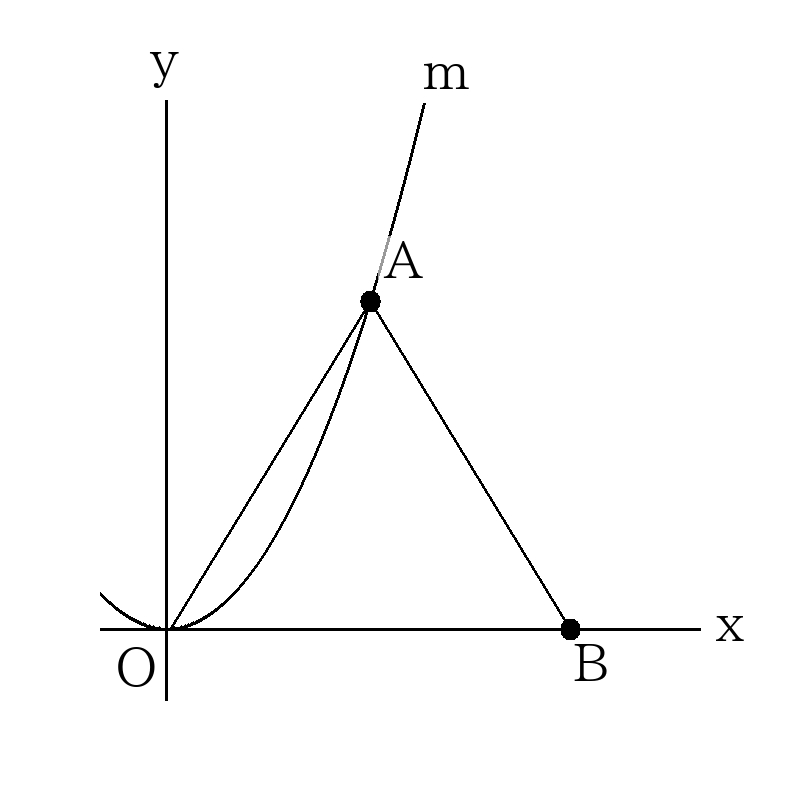
- 点\(A\)は放物線\(m:y=ax^2 ( a> 0 )\)上の点である。三角形\(OAB\)が正三角形になるように点\(B\)をとる。
- 点\(B\)の座標を\(a\)を用いて表しなさい。
- \( \triangle ABC \) の重心の座標を\(a\)を用いて表しなさい。
- \(a\)が変化するとき、\( \triangle ABC \) の重心はある直線上を動くという。この直線の式を求めなさい。
- 媒介変数が苦手な人は基本的な問題集で慣れておくこと!
- 軌跡を求める→媒介変数の文字を代入法で消去
例) \(P(2a+3,-a+4)\)で表されるとき、点\(P\)が動く軌跡を求めると、
\(x=2a+3 \dots ①\)、\(y=-a+4 \dots ②\)と表し
\(①\)を\(a=\dfrac{x-3}{2}\)と変形し\(②\)に代入
\( y=- \left( \dfrac{x-3}{2} \right) +4 \)
式を整理すると
\( y=- \dfrac{x}{2}x + \dfrac{11}{2} \)
よって点\(P\)は\( y=- \dfrac{x}{2}x + \dfrac{11}{2} \)上を動く。
- 点\(A\)は放物線\(m:y=ax^2 ( a> 0 )\)上の点である。点\( B(-2,0) \)をとり、三角形\(ABC\)が正三角形になるように点\(C\)をとる。
- 点\(B\)の座標を\(a\)を用いて表しなさい。
- \( \triangle ABC \) の重心の座標を\(a\)を用いて表しなさい。
- \(a\)が変化するとき、\( \triangle ABC \) の重心はある直線上を動くという。この直線の式を求めなさい。
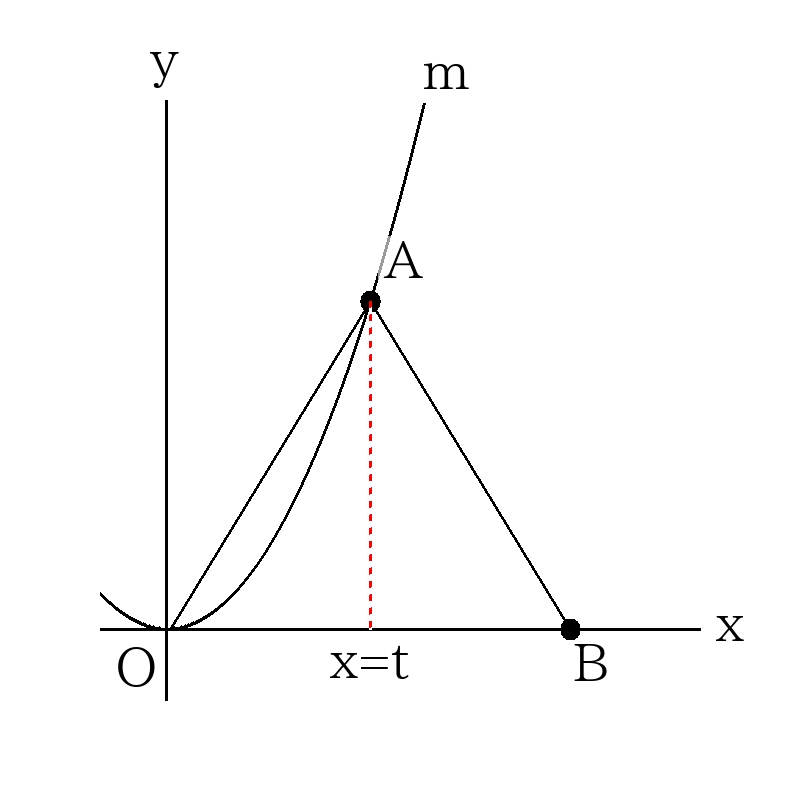
正三角形の長さの比より、\(A\)の\(x\)座標を\(x=t\)とすると、\(A\)の\(y\)座標は\( \sqrt{3}t \)
点\(A\)は放物線\(y=ax^2\)上にあるので代入すると、
\( \sqrt{3}t=at^2 \)
\(t \neq 0 \)より
\( at=\sqrt{3} \)
\( t=\dfrac{\sqrt{3}}{a} \)
よって点\(B\)の\(x\)座標は\(2t=\dfrac{2 \sqrt{3}}{a}\)
\(B \left( \dfrac{2 \sqrt{3}}{a},0 \right) \)
重心の位置の\(y\)座標は点\(A\)の\(y\)座標の\(\dfrac{1}{3} \)のところにある。
点\(A\)の座標は\( A\left( \dfrac{ \sqrt{3}}{a},\dfrac{3}{a} \right) \)なので、
\(G \left( \dfrac{ \sqrt{3}}{a}, \dfrac{1}{a} \right) \)
\(a\)を消去すれば良い。
①は
\(x= \dfrac{1}{a} \times \sqrt{3} \)
②の\( \dfrac{1}{a}=y\)を代入すると
\(x=y \times \sqrt{3} \)
式を整理すると
\(y= \dfrac{ \sqrt{3}}{3}x \)



コメント