さまざまな図形
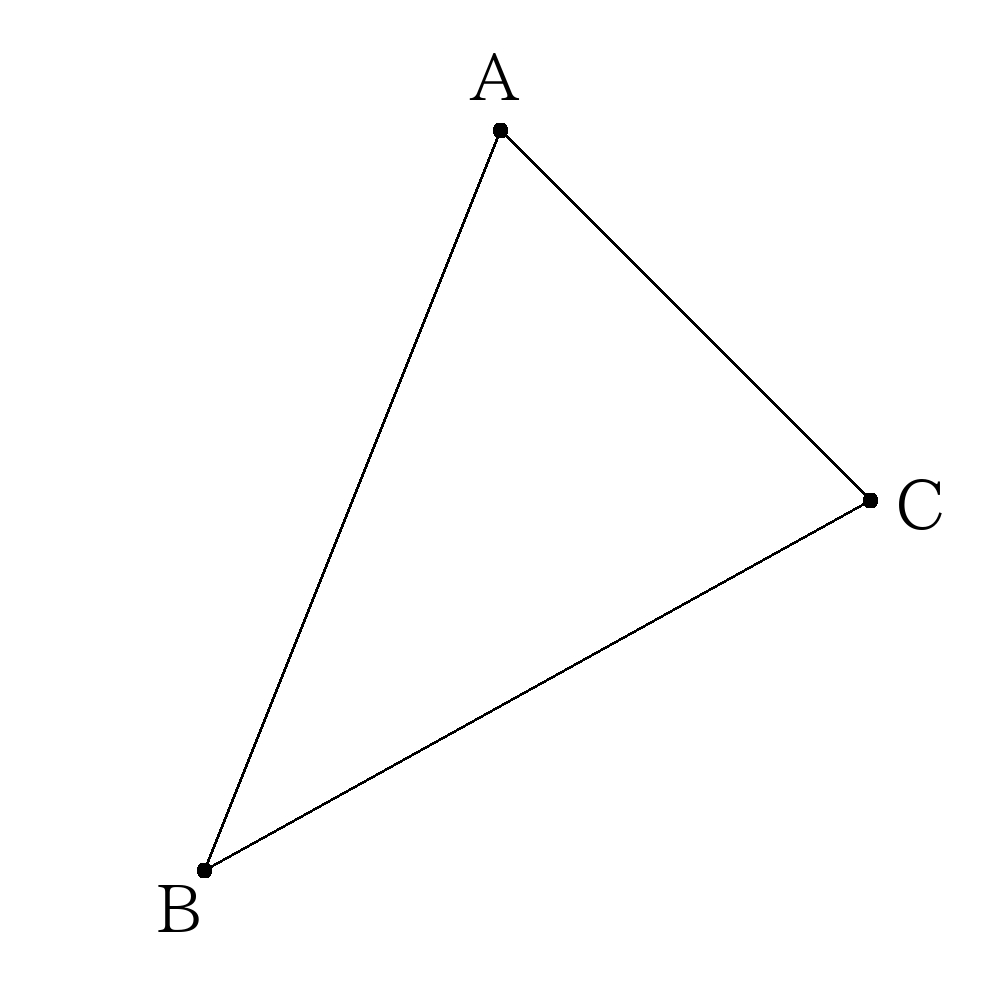
- 次の図で\(A(4,8),B(1,2),C(9,4)\)である。点\(C\)を通り\(\triangle ABC\)を二等分する直線の式を求めなさい。
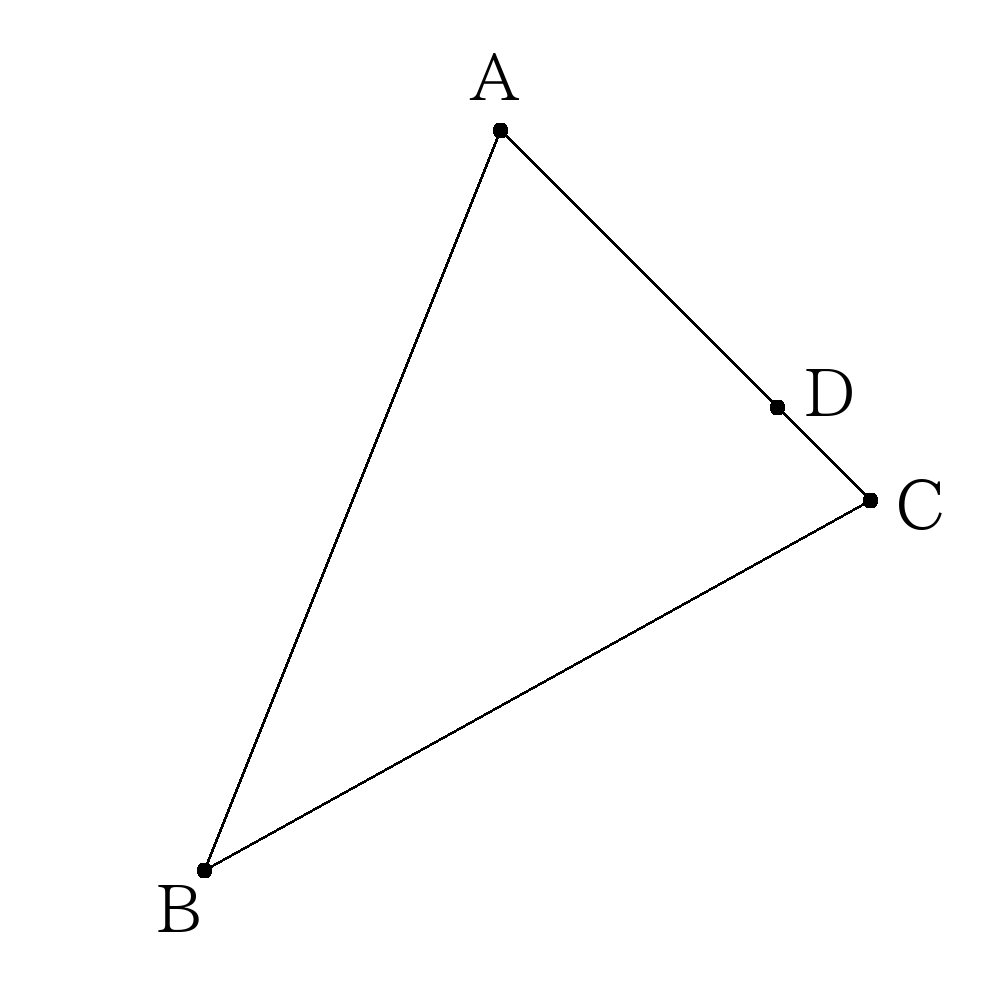
- 次の図で\(A(4,8),B(1,2),C(9,3),D\left(7,5\right)\)で、点\(D\)は線分\(AC\)上の点である。点\(D\)を通り\(\triangle ABC\)を二等分する直線の式を求めなさい。
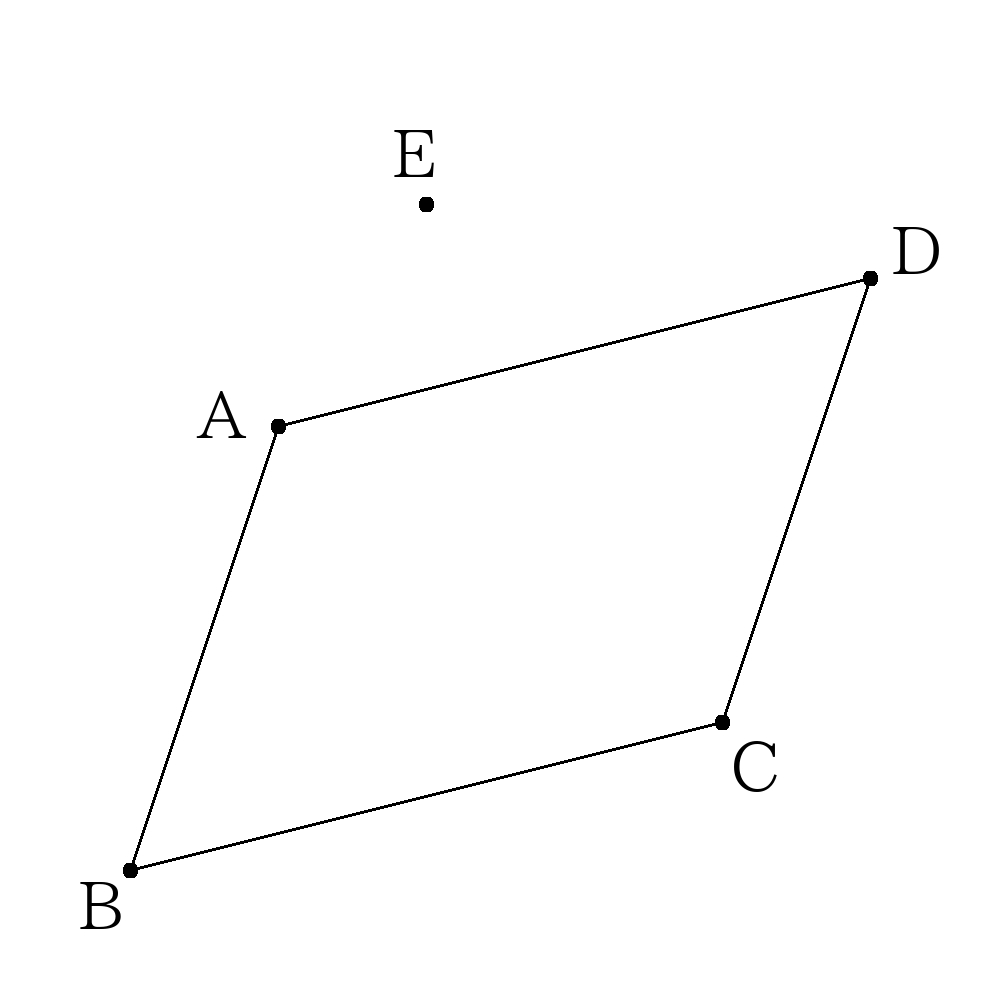
- 次の図で\(A(3,7),B(1,1),C(9,3),D(11,9),E(5,10)\)であり、点\(E\)を通り平行四辺形\(ABCD\)を二等分する直線の式を求めなさい。
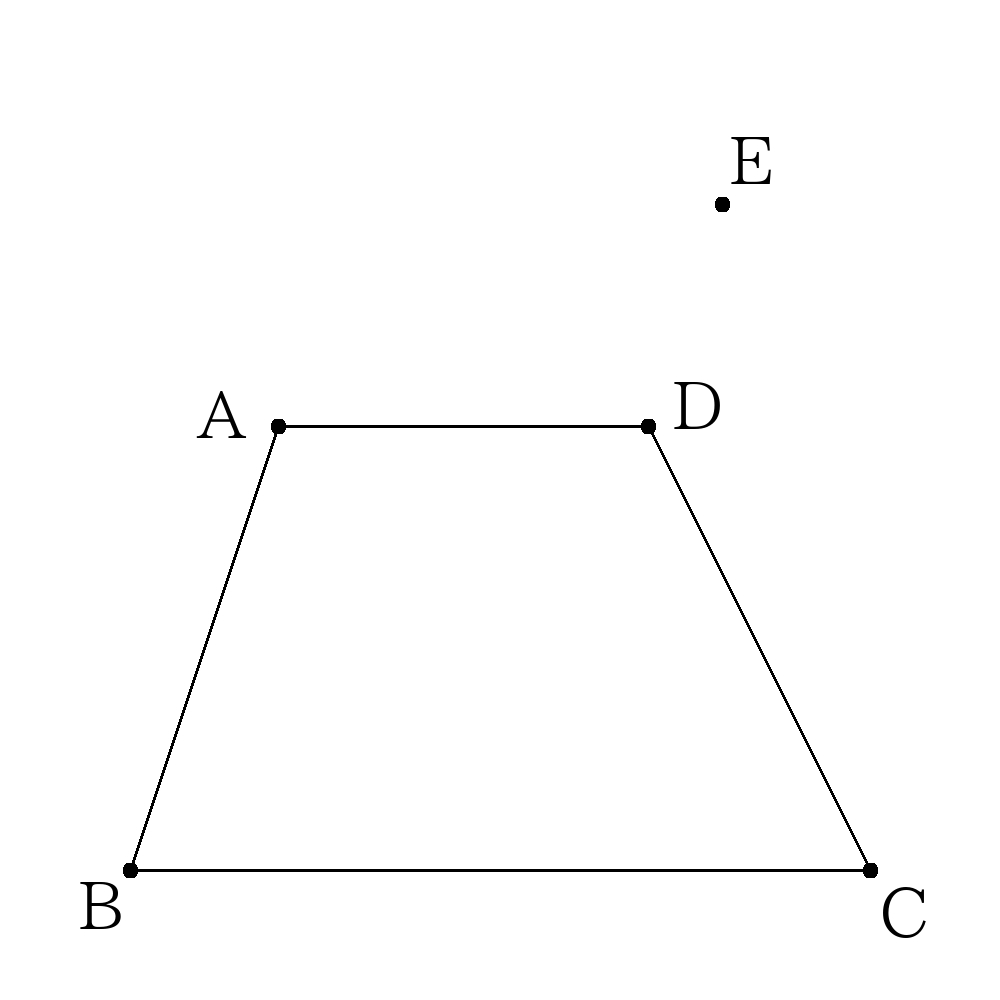
- 次の図で\(A(3,7),B(1,1),C(11,1),D(8,7),E(9,10)\)であり、点\(E\)を通り台形\(ABCD\)を二等分する直線の式を求めなさい。
- 次の図で\(A(3,7),B(1,1),C(11,1),D(8,7),E\left(9,5\right)\)であり、点\(E\)を通り台形\(ABCD\)を二等分する直線の式を求めなさい。
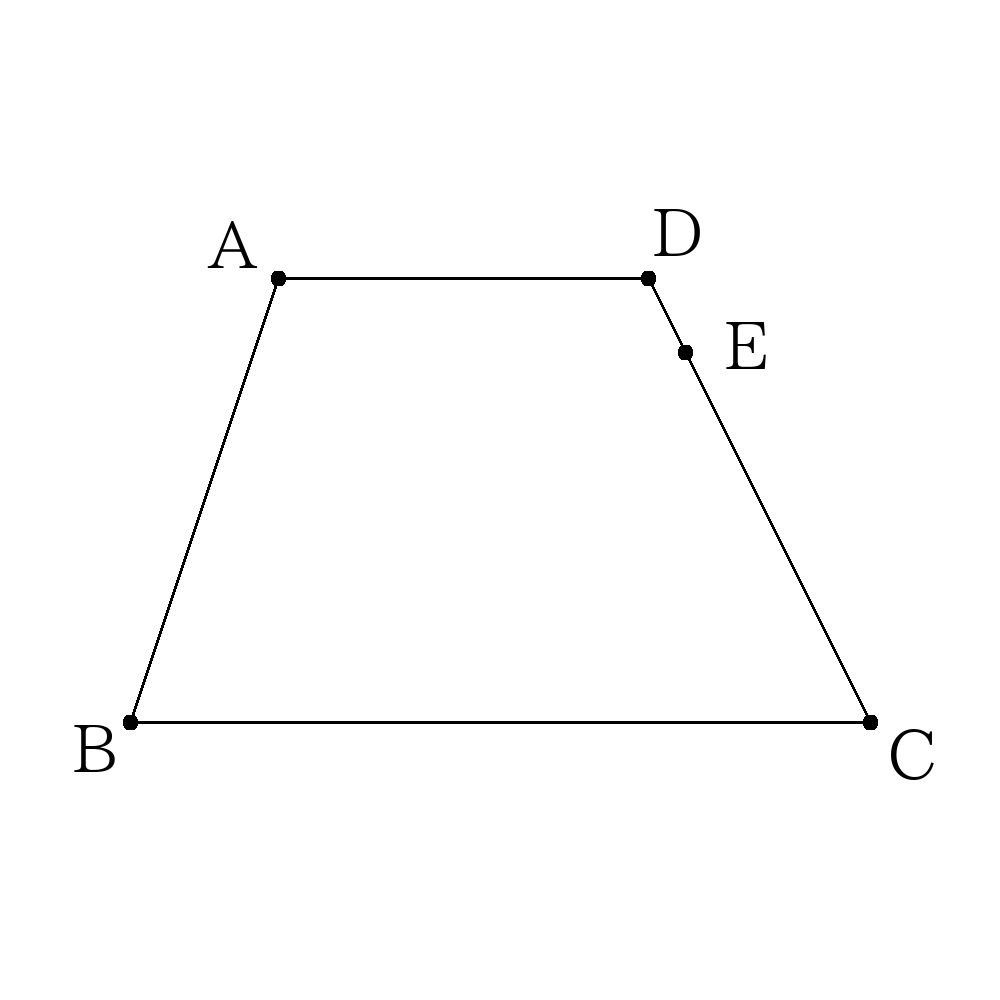
- それぞれの図形の二等分する方法を覚えておく!
三角形の二等分(頂点を通るとき)
底辺の中点を通るように直線を求める。
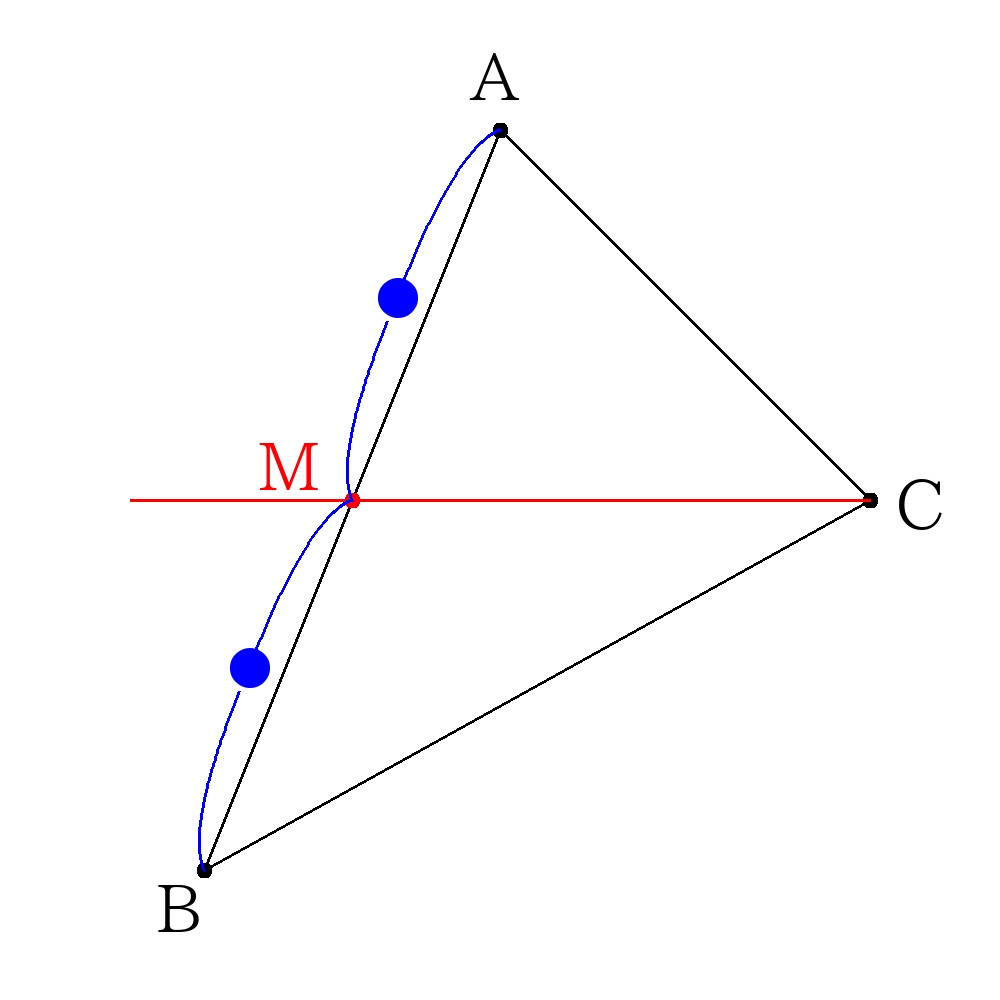
三角形の二等分(頂点を通らないとき)
共通角を挟む2辺の比の積から計算する。
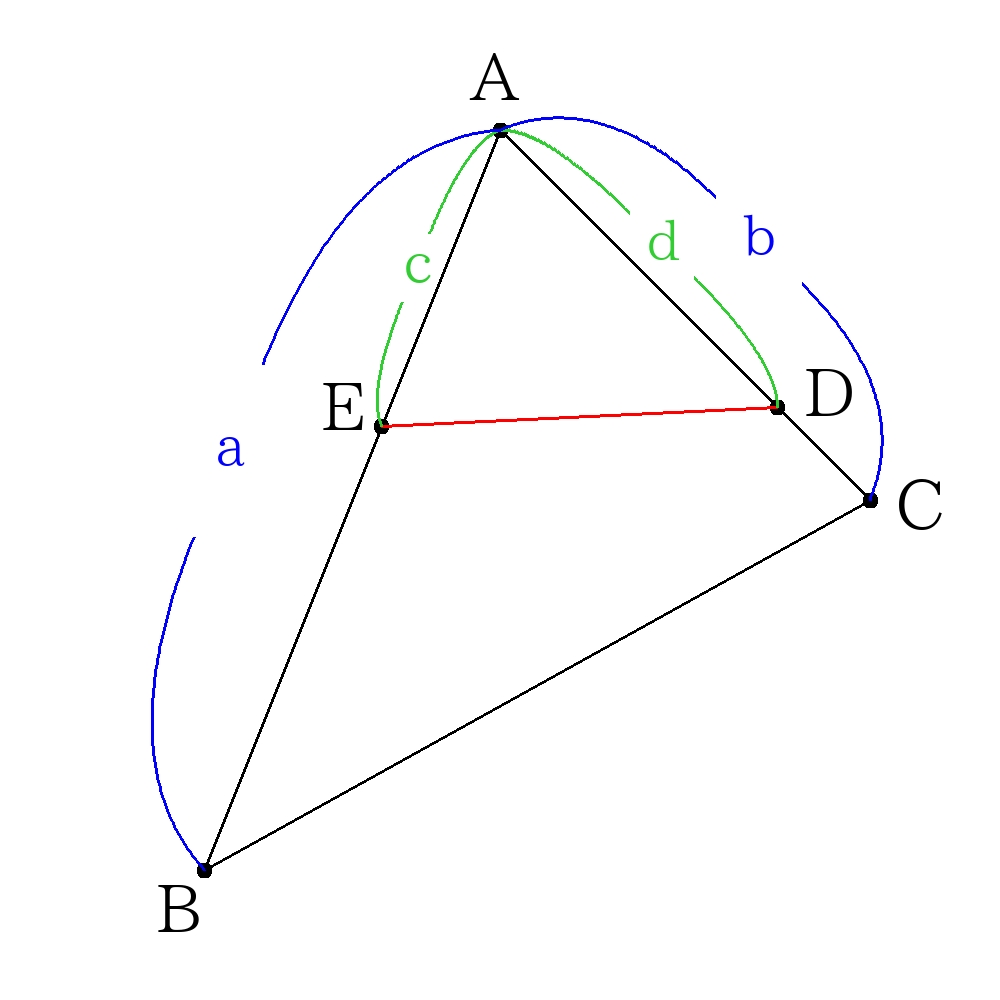
面積比は\( \triangle ABC : \triangle AED=(a \times b): (c \times d) \)で決まる。
また、\(\triangle AED=\triangle ABC \times \dfrac{c}{a} \times \dfrac{d}{b}\)と表すこともできる。
\( \triangle AED\)が\( \triangle ABC\)の半分になるためには
\( \dfrac{c}{a} \times \dfrac{d}{b}=\dfrac{1}{2} \)を満たせば良い。
平行四辺形の二等分
対角線の交点(対角線の中点)を通るように直線を求める。
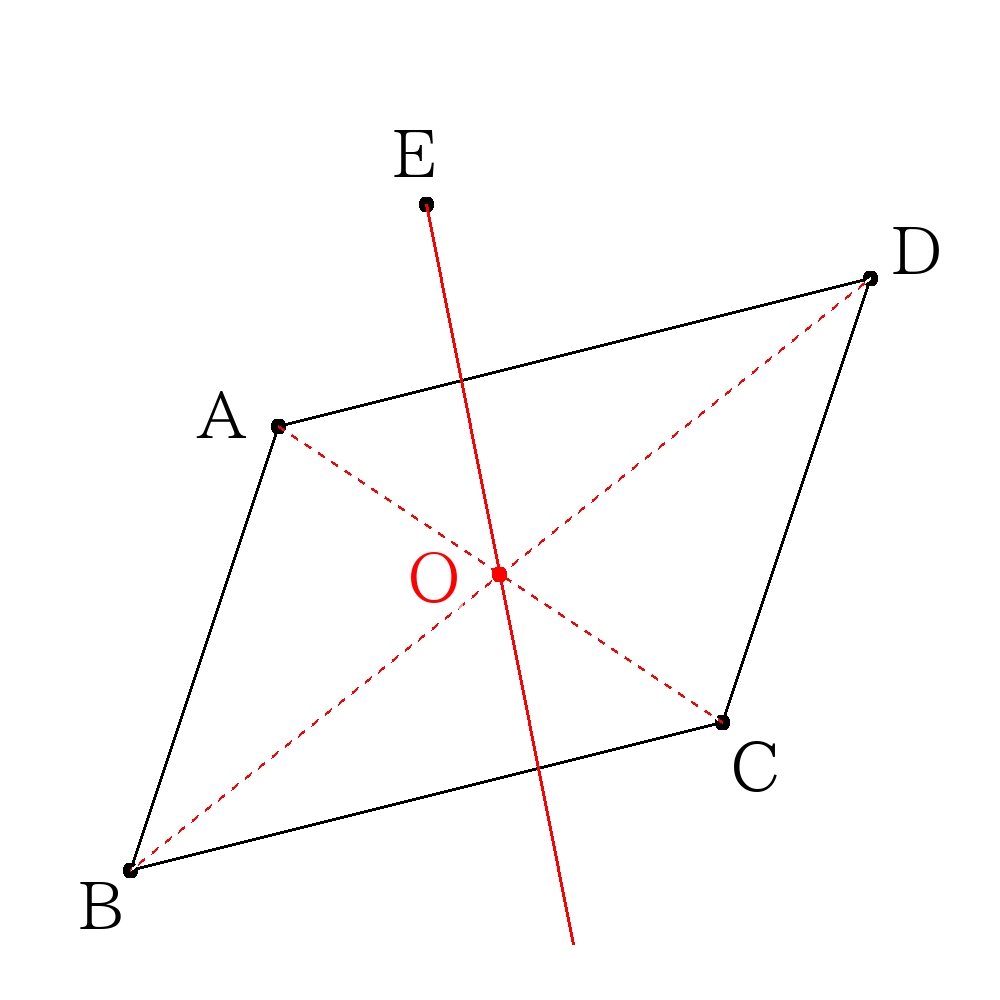
※対角線の交点を通る直線で平行四辺形を分けると、面積が二等分することは三角形の合同から証明できる。
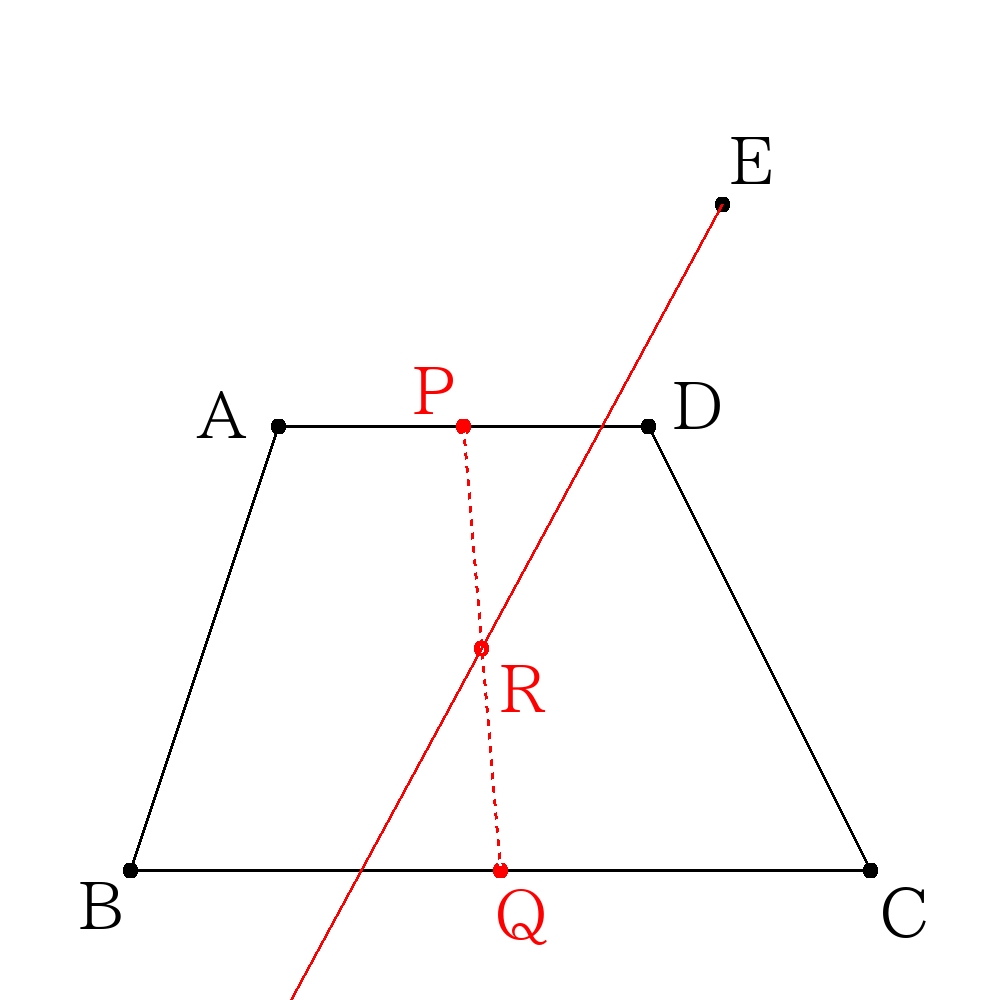
台形の二等分(上底と下底を通るとき)
上底の中点\(P\)と下底の中点\(Q\)を求め、さらに線分\(PQ\)の中点\(R\)を求める。
点\(R\)を通るように直線を求めれば良い。
その他
面積の半分を求め、その面積から長さを計算する。
- 次の図で\(A(4,8),B(1,2),C(9,4)\)である。点\(C\)を通り\( \triangle ABC \)を二等分する直線の式を求めなさい。
- 次の図で\(A(4,8),B(1,2),C(9,3),D\left(7,5\right)\)で、点\(D\)は線分\(AC\)上の点である。点\(D\)を通り\( \triangle ABC \)を二等分する直線の式を求めなさい。
- 次の図で\(A(3,7),B(1,1),C(9,3),D(11,9),E(5,10)\)であり、点\(E\)を通り平行四辺形\( ABCD \)を二等分する直線の式を求めなさい。
- 次の図で\(A(3,7),B(1,1),C(11,1),D(8,7),E(9,10)\)であり、点\(E\)を通り台形\( ABCD \)を二等分する直線の式を求めなさい。
- 次の図で\(A(3,7),B(1,1),C(11,1),D(8,7),E\left(9,5\right)\)であり、点\(E\)を通り台形\( ABCD \)を二等分する直線の式を求めなさい。
底辺の中点を通るように直線を求めれば良い。

線分\(AB\)の中点\(M\)は
\(M \left( \dfrac{4+1}{2} , \dfrac{8+2}{2} \right)\)
\(=M \left( \dfrac{5}{2} , 5 \right)\)
直線\(MC\)の式は
\( y=\dfrac{4-5}{9-\dfrac{5}{2}}(x-9)+4 \)
\( y=-\dfrac{2}{13}(x-9)+4 \)
\(y=- \dfrac{2}{13}x+ \dfrac{60}{13} \)
※直線の式は連立方程式で求めても良いが、傾きと定点公式から求める習慣をつけておきましょう。
角\(A\)を挟み込む2辺の比の積から求める。

\(a:c\)や\(b:d\)のように斜めの直線の長さの比は、\(x\)座標もしくは\(y\)座標の差から求められる。
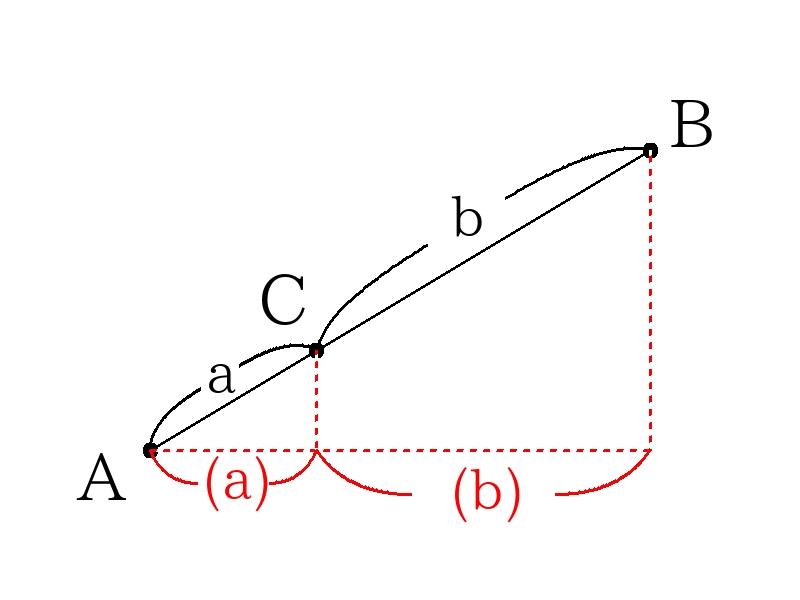
\(b:d=(9-4):(7-4)=5:3\)
よって、\( \dfrac{d}{b}=\dfrac{3}{5}\)
面積を二等分するので、
\( \dfrac{c}{a} \times \dfrac{d}{b}=\dfrac{1}{2}\)
\( \dfrac{c}{a} \times \dfrac{3}{5}=\dfrac{1}{2}\)
\( \dfrac{c}{a} =\dfrac{5}{6}\)
よって、点\(E\)の座標は
\(E\left(4+\dfrac{5}{6}(1-4),8+\dfrac{5}{6}(2-8) \right)\)
\(=E\left(\dfrac{3}{2},3 \right)\)
\(D\left(7,5\right)\)、\(E\left(\dfrac{3}{2},3 \right)\)を通る直線の式を求めると、
\(y= \dfrac{4}{11}x+ \dfrac{27}{11} \)
※点\(E\)の座標は線分\(AB\)の\(x\)の長さ,\(y\)方向の長さから計算すれば良い。

対角線の交点を通る直線を求めればよい。
点\(O\)は線分\(AC\)の中点なので、
\(O\left(\dfrac{3+9}{2},\dfrac{7+3}{2}\right)\)
\(=O\left(6,5\right)\)
\(E(5,10)\)と\(O\left(6,5\right)\)を通る直線の式を求めれば良いので
\( y=\dfrac{5-10}{6-5}(x-5)+10\)
\(y=-5x+35 \)

上底の中点\(P\)と下底の中点\(Q\)の中点\(R\)を通る直線を求めれば良い。
\( P\left( \dfrac{3+8}{2}, \dfrac{7+7}{2} \right)=P\left( \dfrac{11}{2}, 7 \right) \)
\( Q\left( \dfrac{1+11}{2}, \dfrac{1+1}{2} \right)=Q\left( 6, 1 \right) \)
\(R\)は\(P\)と\(Q\)の中点なので、
\( R\left( \dfrac{ \dfrac{11}{2}+6}{2}, \dfrac{7+1}{2} \right)=R\left( \dfrac{23}{4}, 4 \right) \)
\(E(9,10)\)と\(R\left( \dfrac{23}{4}, 4 \right)\)を通る直線の式を求めれば良いので、
\(y=\dfrac{4-10}{\dfrac{23}{4}-9}(x-9)+10\)
\(y=\dfrac{24}{13}(x-9)+10\)
\(y= \dfrac{24}{13}x- \dfrac{86}{13} \)
二等分しそうな線を予測して線を引く。※注
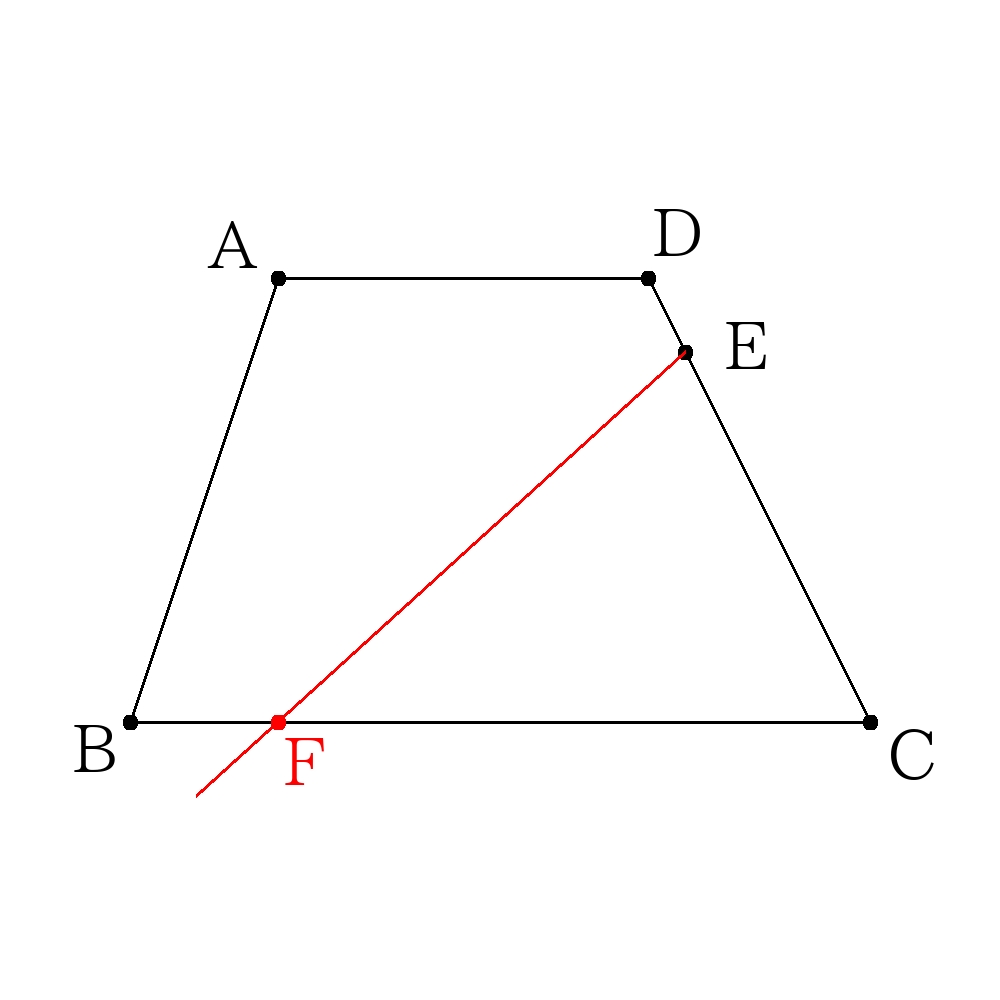
\(E\)を通り台形\(ABCD\)の面積を二等分する直線と\(BC\)との交点を\(F\)とする。
ここで台形\(ABCD\)の面積を計算すると
\( (5+10) \times 6 \times \dfrac{1}{2}=45 \)
面積が半分になるので、
\(\triangle EFC=\dfrac{45}{2} \)になれば良い。
\(FC \times 5 \times \dfrac{1}{2}=\dfrac{45}{2}\)
\(FC=9\)
よって\(F\)の座標は\( F(2,1) \)
\(EF\)の直線の式は
\( y=\dfrac{5-1}{9-2}(x-2)+1 \)
\( y=\dfrac{4}{7}(x-2)+1 \)
\(y= \dfrac{4}{7}x- \dfrac{1}{7} \)
※注)予測する上で判断が難しいときは簡単に計算すること。
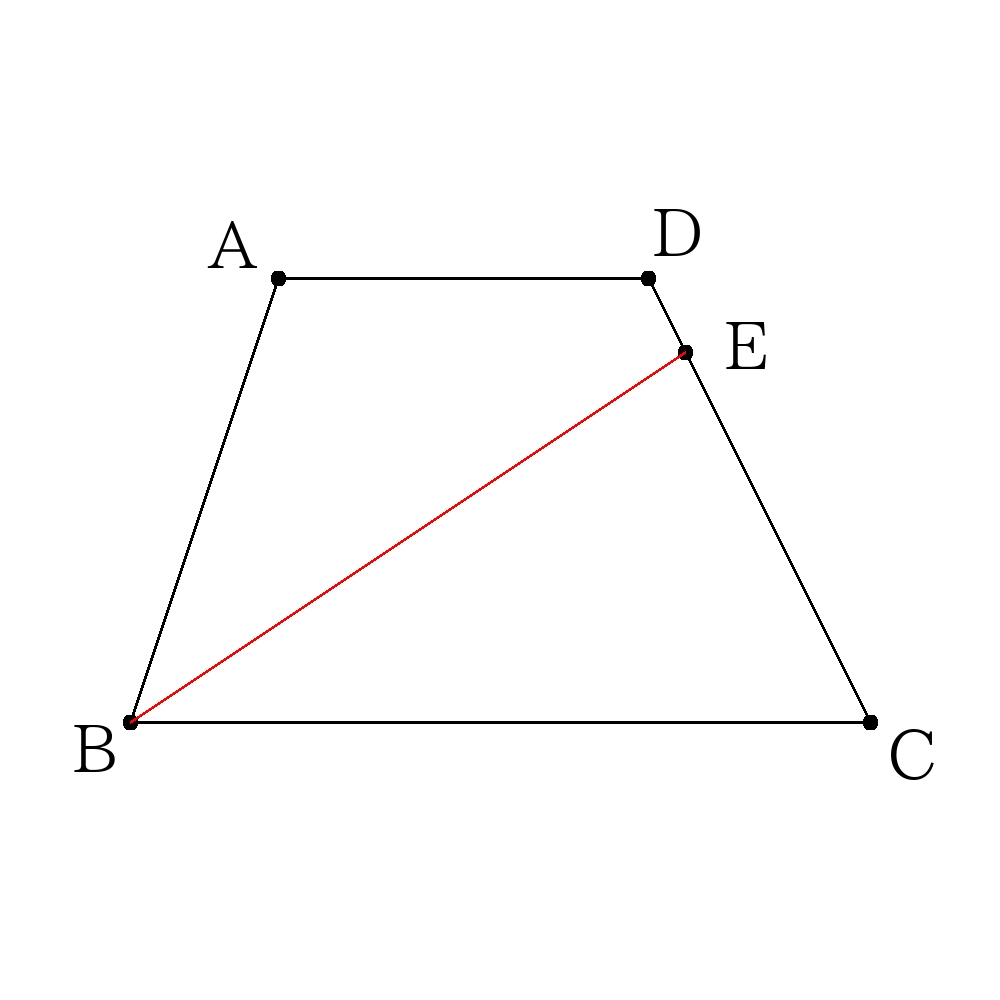
台形の半分は\(ABCD=\dfrac{45}{2}=22.5\)
\( \triangle BEC= 30\)
よって、二等分する直線は\(B\)の右側(\(C\)寄り)を通ることがわかる。



コメント