回転体の体積
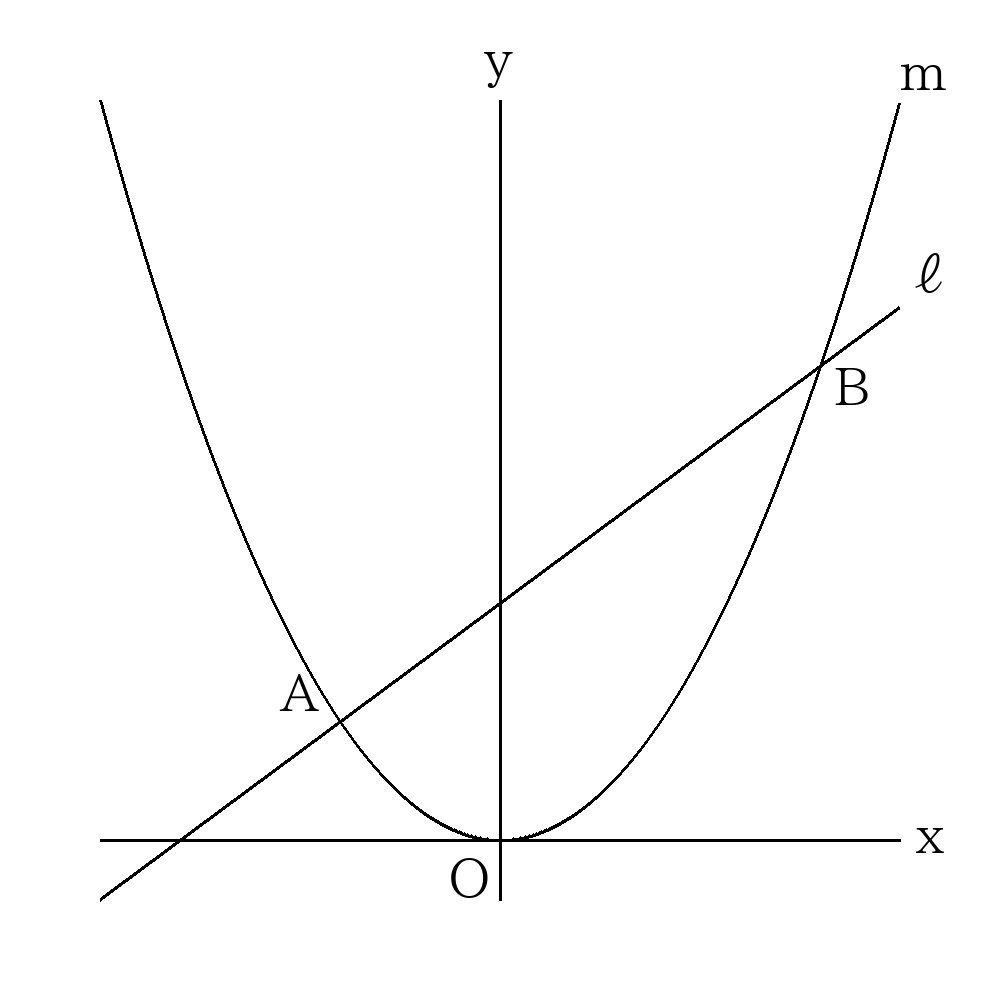
- 放物線\(m:y=x^2\)と直線\(ℓ:y=x+6\)が次の図のように2点\(A,B\)で交わっている。
-
\( x \)軸を軸として\( \triangle AOB \)を1回転してできる回転体の体積を求めなさい。
-
\( y \)軸を軸として\( \triangle AOB \)を1回転してできる回転体の体積を求めなさい。
- 見取り図を書かないで解けるようにする。
- 高さの和/高さの差を利用すること。
高さの和/高さの差の利用
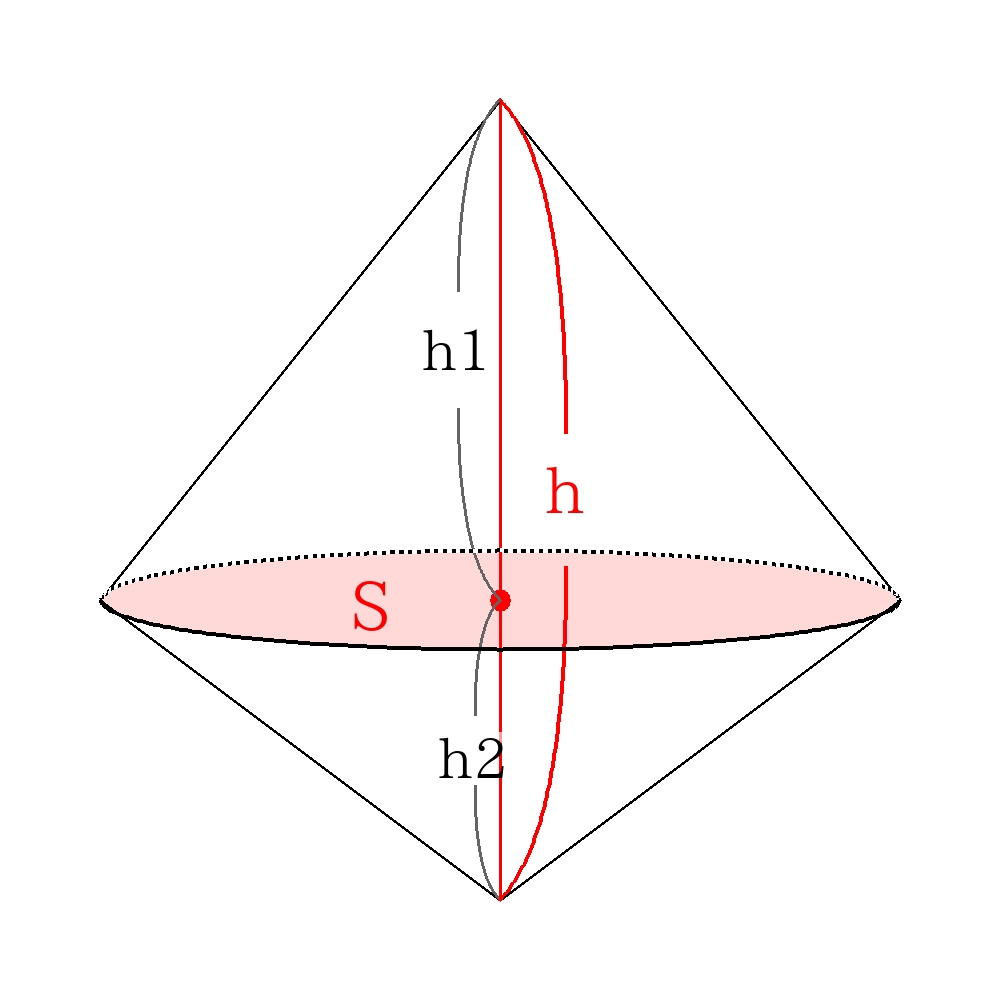
図のように底面積が共通な図形の体積の合計は
\(V=S \times h1 \times \dfrac{1}{3}+S \times h2 \times \dfrac{1}{3}\)
\(=S \times ( \color{red}{h1 +h2} ) \times \dfrac{1}{3}\)
\(=S \times h \times \dfrac{1}{3}\)
のように高さの和を利用すること。
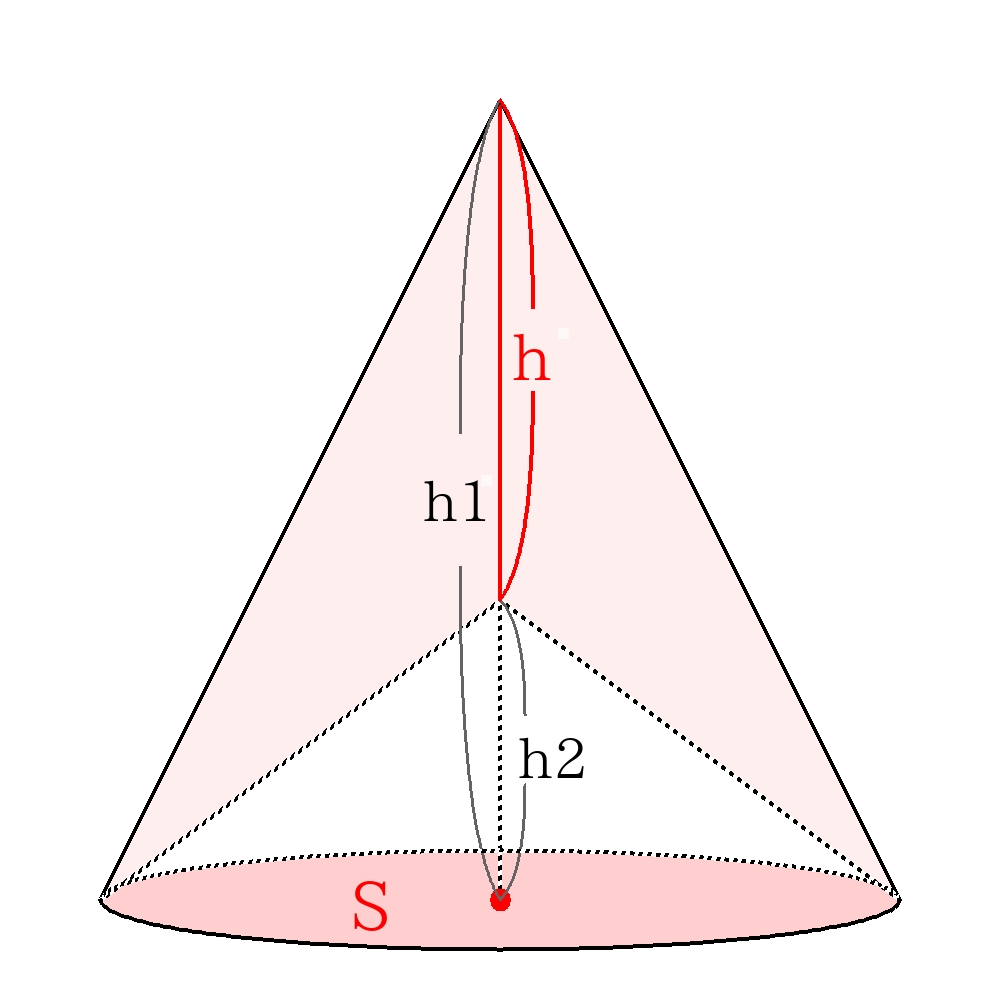
図のように底面積が共通な図形の体積の差は
\(V=S \times h1 \times \dfrac{1}{3}-S \times h2 \times \dfrac{1}{3}\)
\(=S \times ( \color{red}{h1 -h2} ) \times \dfrac{1}{3}\)
\(=S \times h \times \dfrac{1}{3}\)
のように高さの差を利用すること。
- \( x \)軸を軸として\( \triangle AOB \)を1回転してできる回転体の体積を求めなさい。
-
\( y \)軸を軸として\( \triangle AOB \)を1回転してできる回転体の体積を求めなさい。
\(\begin{eqnarray}\left\{\begin{array}{l}y=x^2 \\ y=x+6\end{array}\right.\end{eqnarray}\)
交点の座標を求めると\(A(-2,4)\)、\(B(3,9)\)
求めるべき体積を図示する。(理解のため見取り図も図示するが、実際は書かないで良い。)
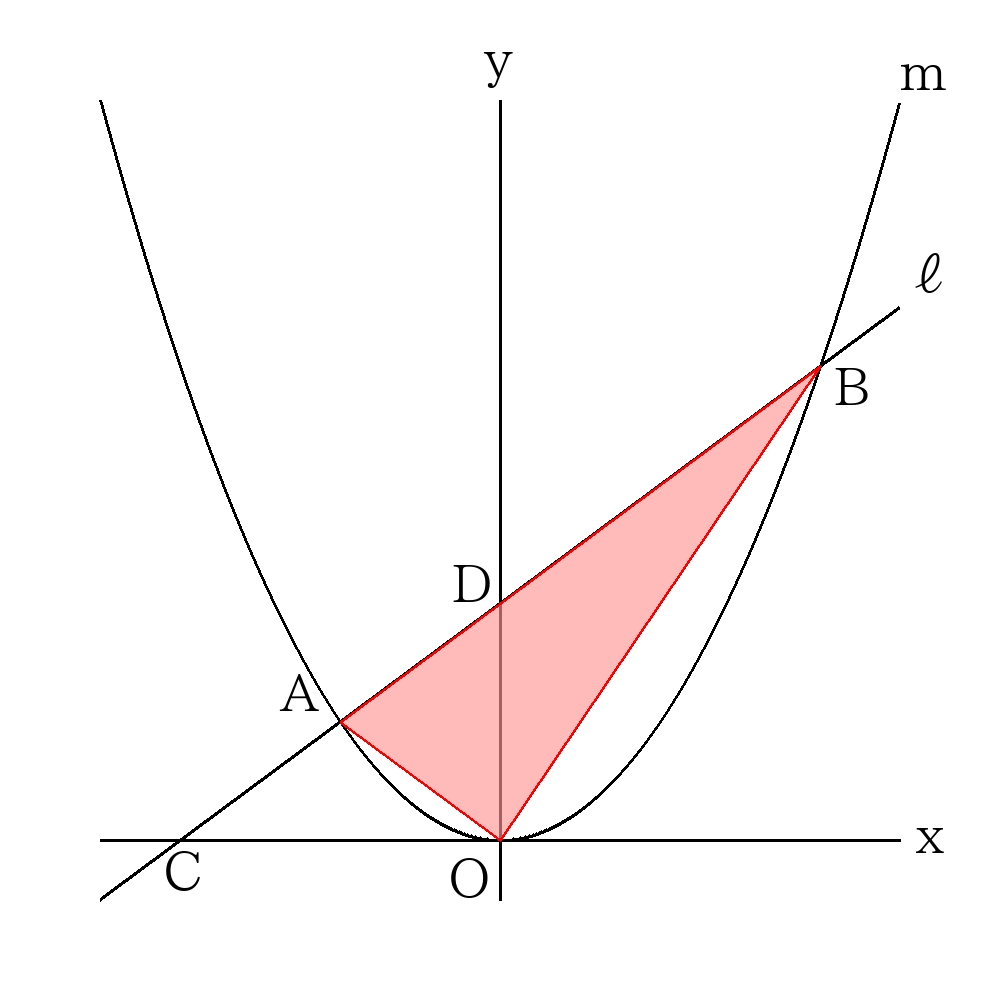
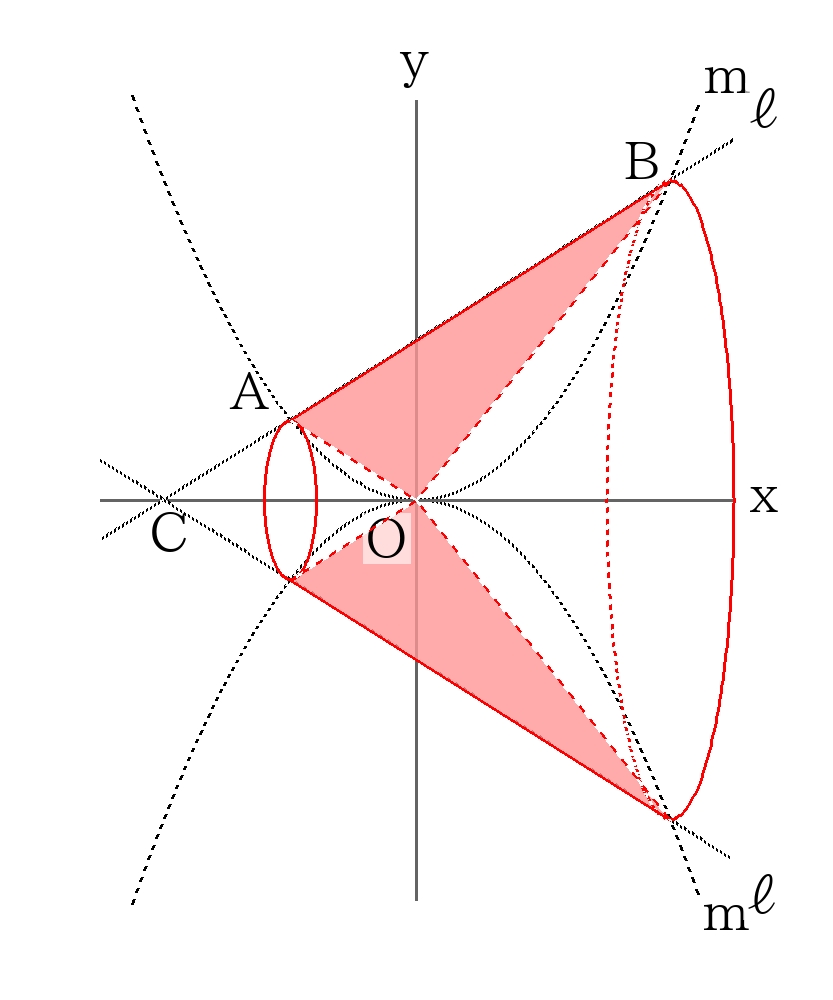
\(y=x+6\)より\(C(-6,0)\)
\( ( \triangle AOBの回転体) = ( \triangle COBの回転体) -( \triangle COA の回転体) \)で計算すれば良い。
※\(\triangle COB \)の回転体は高さの差を利用、\( \triangle COA \)の回転体は高さの和を利用
\( ( \triangle COBの回転体)=9^2 \pi \times 6 \times \dfrac{1}{3}= 162 \pi\)
\( ( \triangle COA の回転体) = 4^2 \pi \times 6 \times \dfrac{1}{3} = 32 \pi \)
よって
\( ( \triangle AOBの回転体)=162 \pi – 32 \pi \)
\( =130 \pi \)
\(130 \pi \)
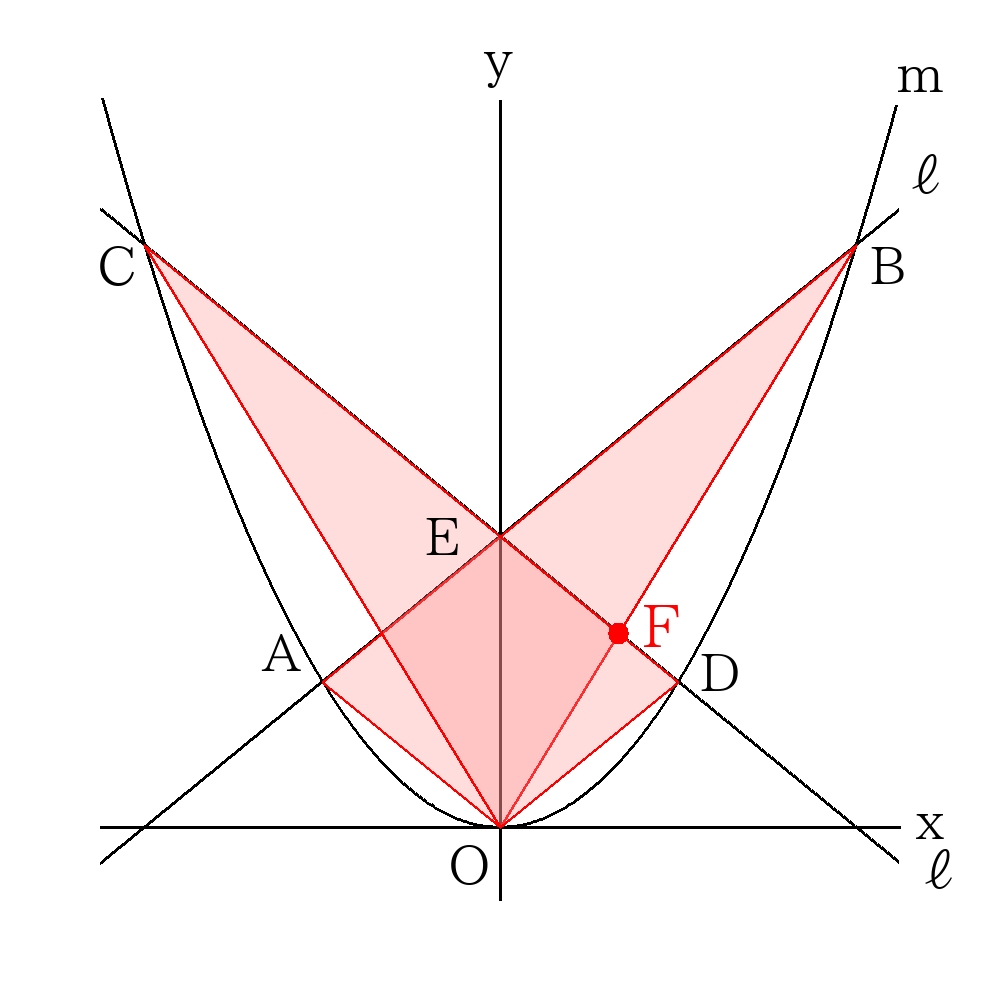
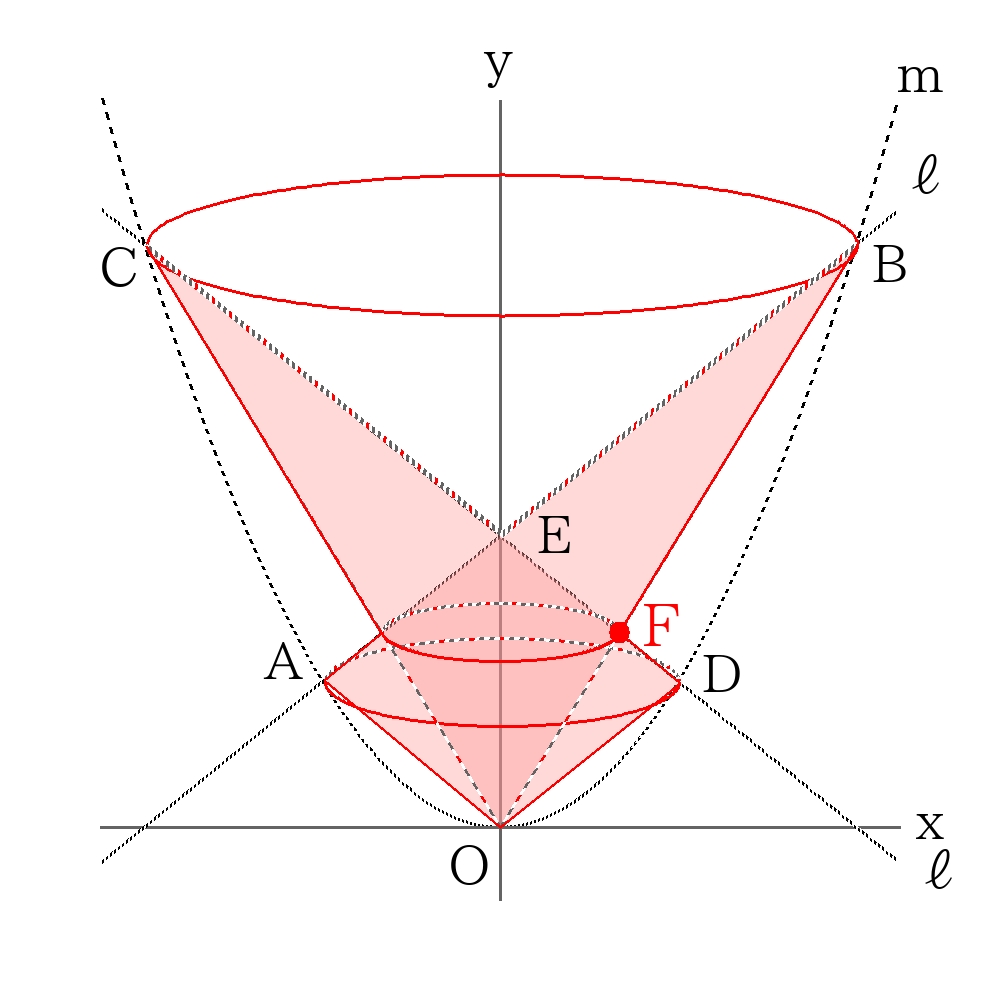
\( ( \triangle AOBの回転体) \)\(= ( \triangle OEDの回転体) + ( \triangle OEB の回転体) -( \triangle OEF の回転体) \)で計算すれば良い。
ここで直線\(OB\)と直線\(CD\)の交点\(F\)を求める。
\(\begin{eqnarray}\left\{\begin{array}{l}y=3x\dots_{(OB)} \\ y=-x+6\dots_{(CD)}\end{array}\right.\end{eqnarray}\)
よって、\(F \left( \dfrac{3}{2} , \dfrac{9}{2} \right)\)
\( ( \triangle OEDの回転体) =2^2 \pi \times 6 \times \dfrac{1}{3}=8 \pi \)
\( ( \triangle OEBの回転体) =3^2 \pi \times 6 \times \dfrac{1}{3}=18 \pi \)
\( ( \triangle OEFの回転体) =\left( \dfrac{3}{2} \right)^2 \pi \times 6 \times \dfrac{1}{3}=\dfrac{9}{2} \pi \)
よって、
\( ( \triangle AOBの回転体)= 8 \pi+ 18 \pi-\dfrac{9}{2} \pi \)
\(= \dfrac{43}{2} \pi\)
\( \dfrac{43}{2} \pi \)



コメント