柱体と錐体
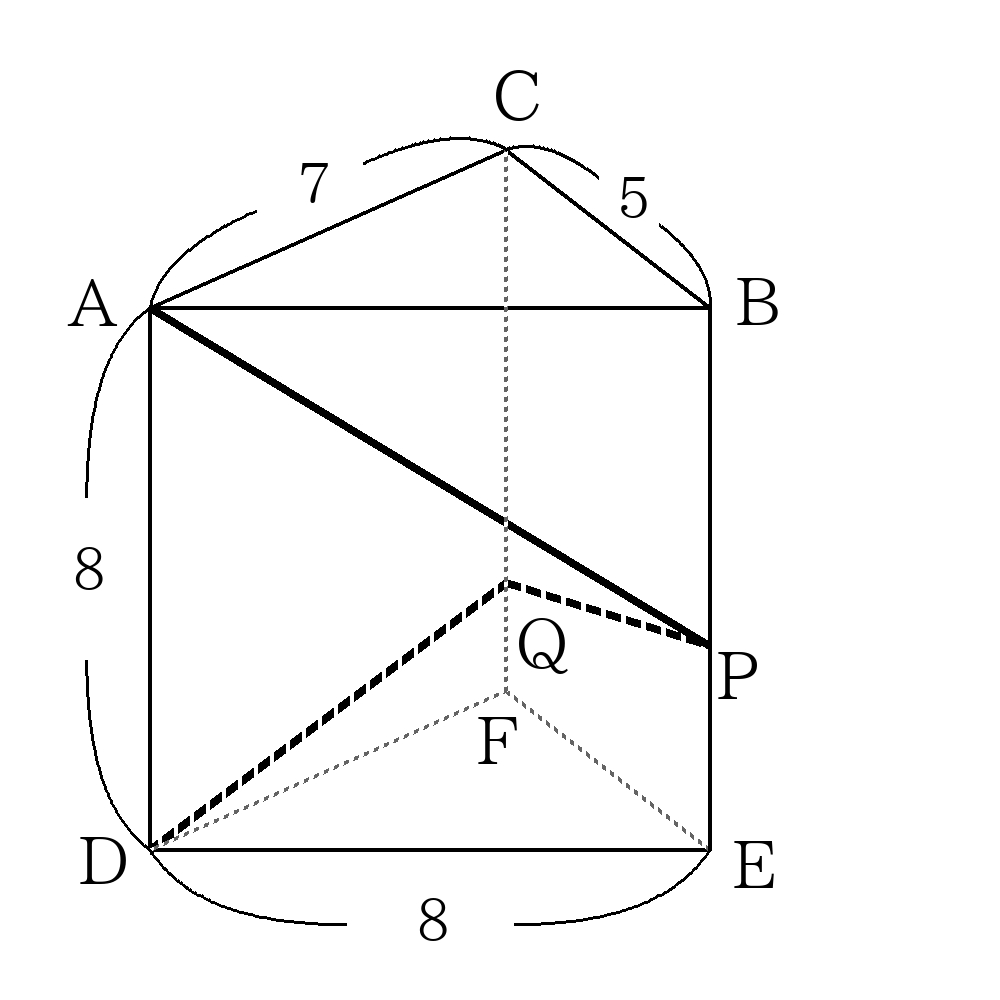
- 下の図の直方体において、\(AP+PQ+QD\)の長さが最短になるとき、線分\(PQ\)の長さを求めなさい。なお、点\(P\)は辺\(BE\)上、点\(Q\)は辺\(CF\)上の点とする。
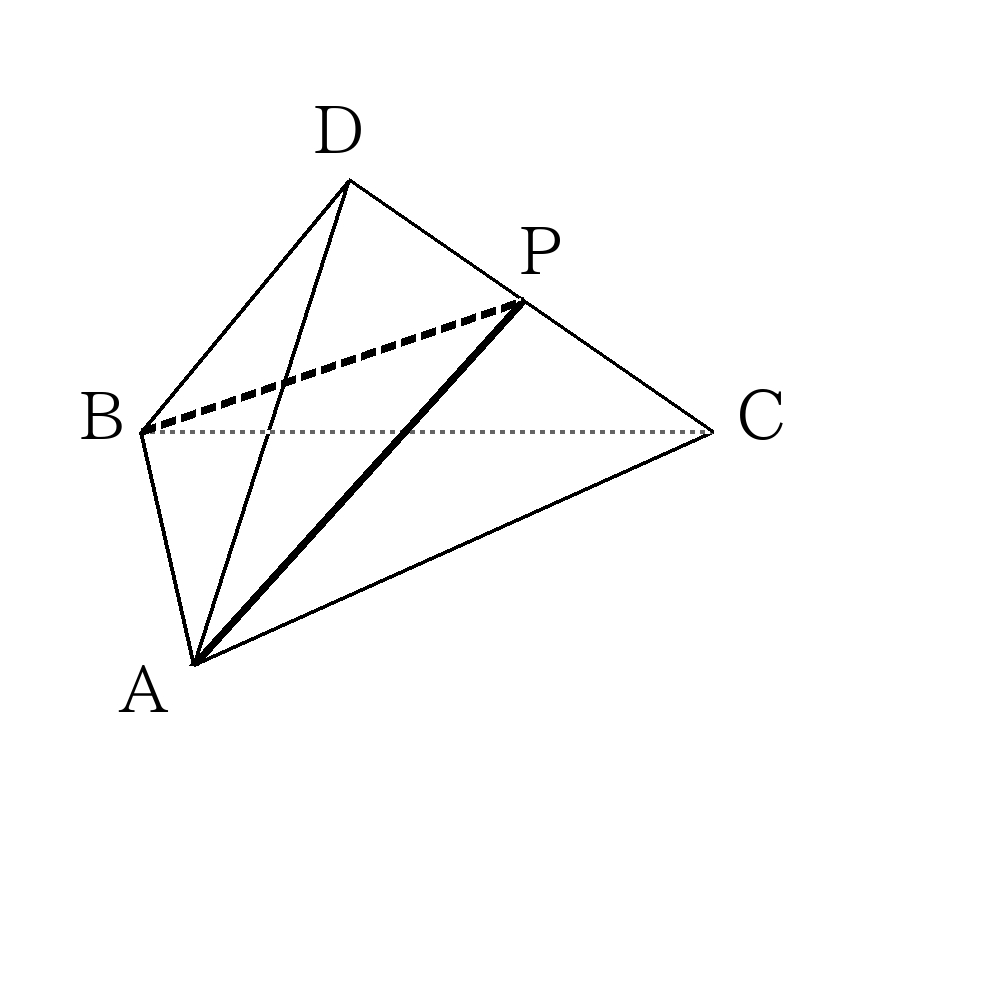
- 下の図は1辺の長さが\(4\)の正四面体である。\(AP+BP\)の長さが最短になるとき、\(AP\)の長さを求めなさい。
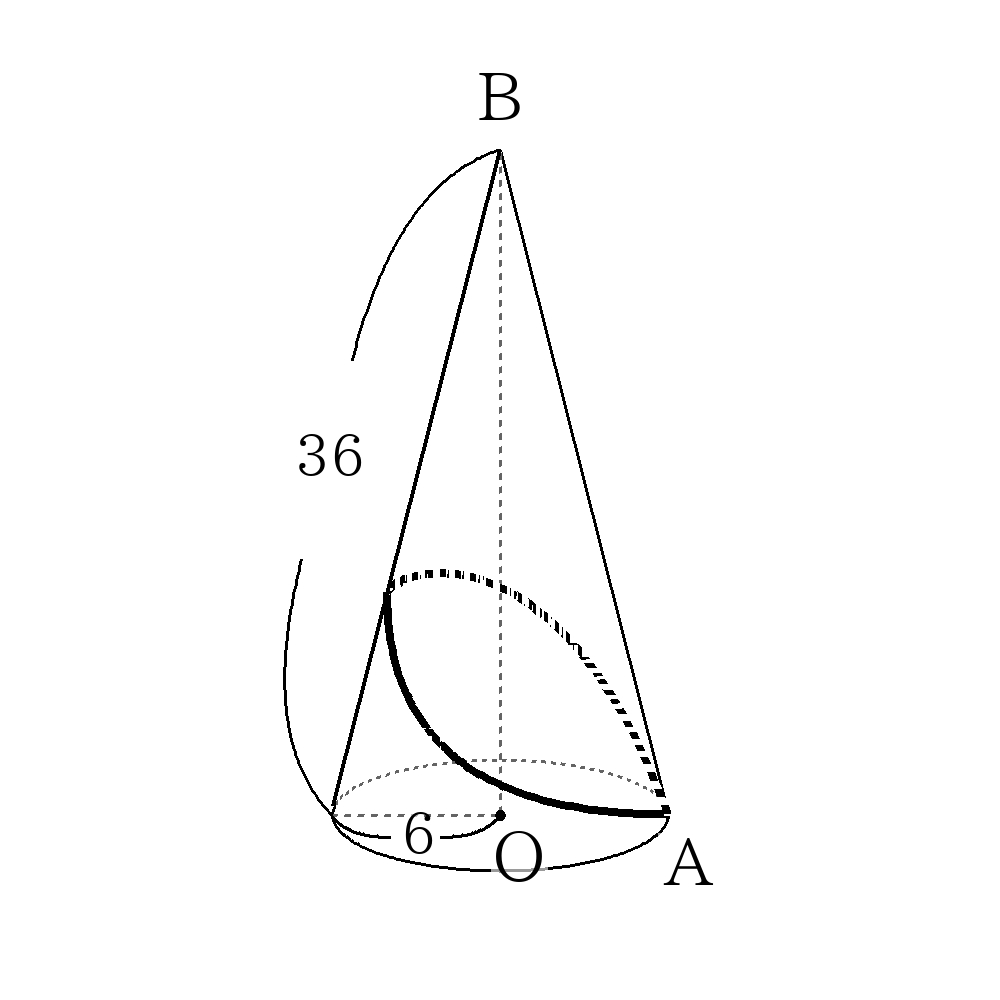
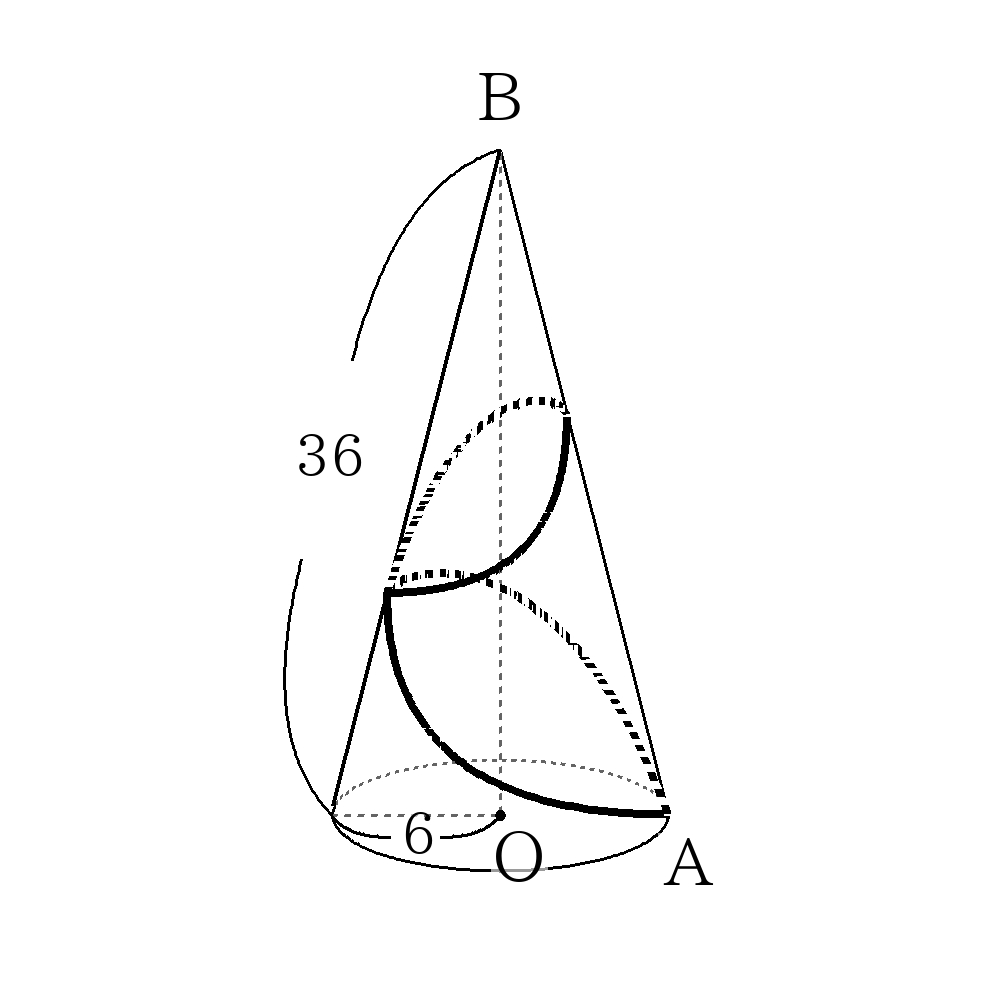
- 下の図のような円錐があり、点\(A\)から始めて点\(A\)にもどるように円錐の側面に沿ってひもをピンと張る。側面を1周まわしたときのひもの長さを\(L\)、側面を2周まわしたときのひもの長さを\(M\)として、\(L\),\(M\)をそれぞれ求めなさい。
- 下の図のような底面の円周が\(18\)、高さが\(12\)の円柱がある。点\(A\)から点\(B\)に円柱の側面に沿ってひもをピンと張る。側面を1周まわしたときのひもの長さを\(L\)、側面を2周まわしたときのひもの長さを\(M\)として、\(L\),\(M\)をそれぞれ求めなさい。
なお、点\(A\),点\(B\)は底面に垂直な同一線上にある。
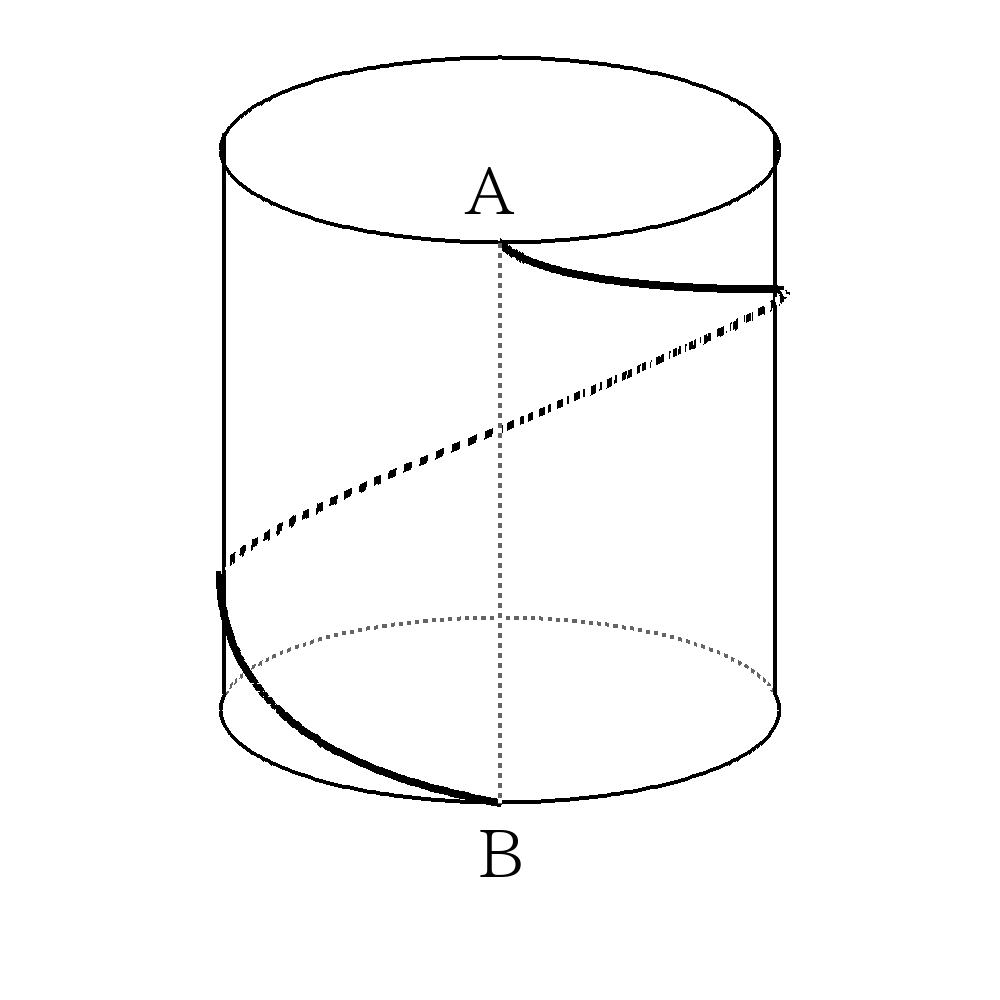
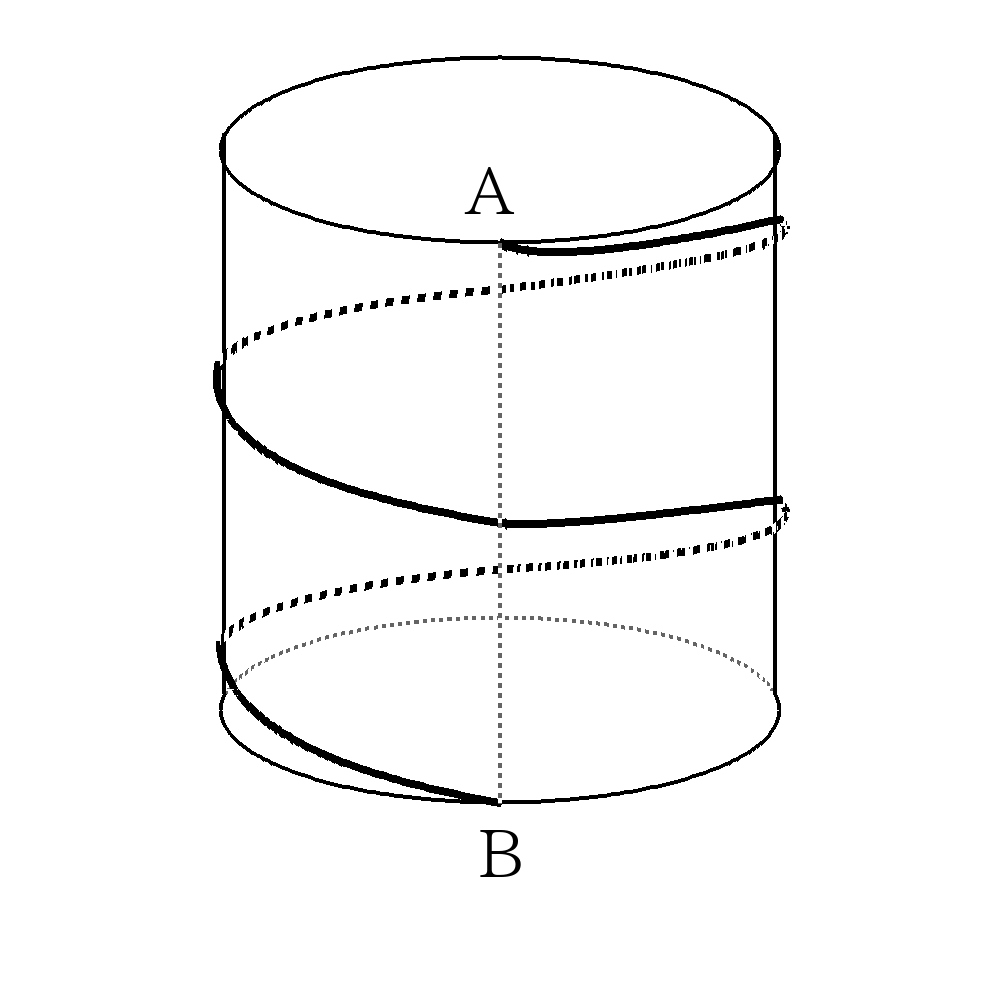
- 展開図を書いて、始点と終点を直線で結ぶ。
※「平面上の最短距離=直線」の考えはすぐに出てくるようにしておくこと。 - 展開図を書くときは実際に通る面だけで良い。
- 下の図の直方体において、\(AP+PQ+QD\)の長さが最短になるとき、線分\(PQ\)の長さを求めなさい。なお、点\(P\)は辺\(BE\)上、点\(Q\)は辺\(CF\)上の点とする。
- 下の図は1辺の長さが\(4\)の正四面体である。\(AP+BP\)の長さが最短になるとき、\(AP\)の長さを求めなさい。
- 下の図のような円錐があり、点\(A\)から始めて点\(A\)にもどるように円錐の側面に沿ってひもをピンと張る。側面を1周まわしたときのひもの長さを\(L\)、側面を2周まわしたときのひもの長さを\(M\)として、\(L\),\(M\)をそれぞれ求めなさい。


- 下の図のような底面の円周が\(18\)、高さが\(12\)の円柱がある。点\(A\)から点\(B\)に円柱の側面に沿ってひもをピンと張る。側面を1周まわしたときのひもの長さを\(L\)、側面を2周まわしたときのひもの長さを\(M\)として、\(L\),\(M\)をそれぞれ求めなさい。
なお、点\(A\),点\(B\)は底面に垂直な同一線上にある。



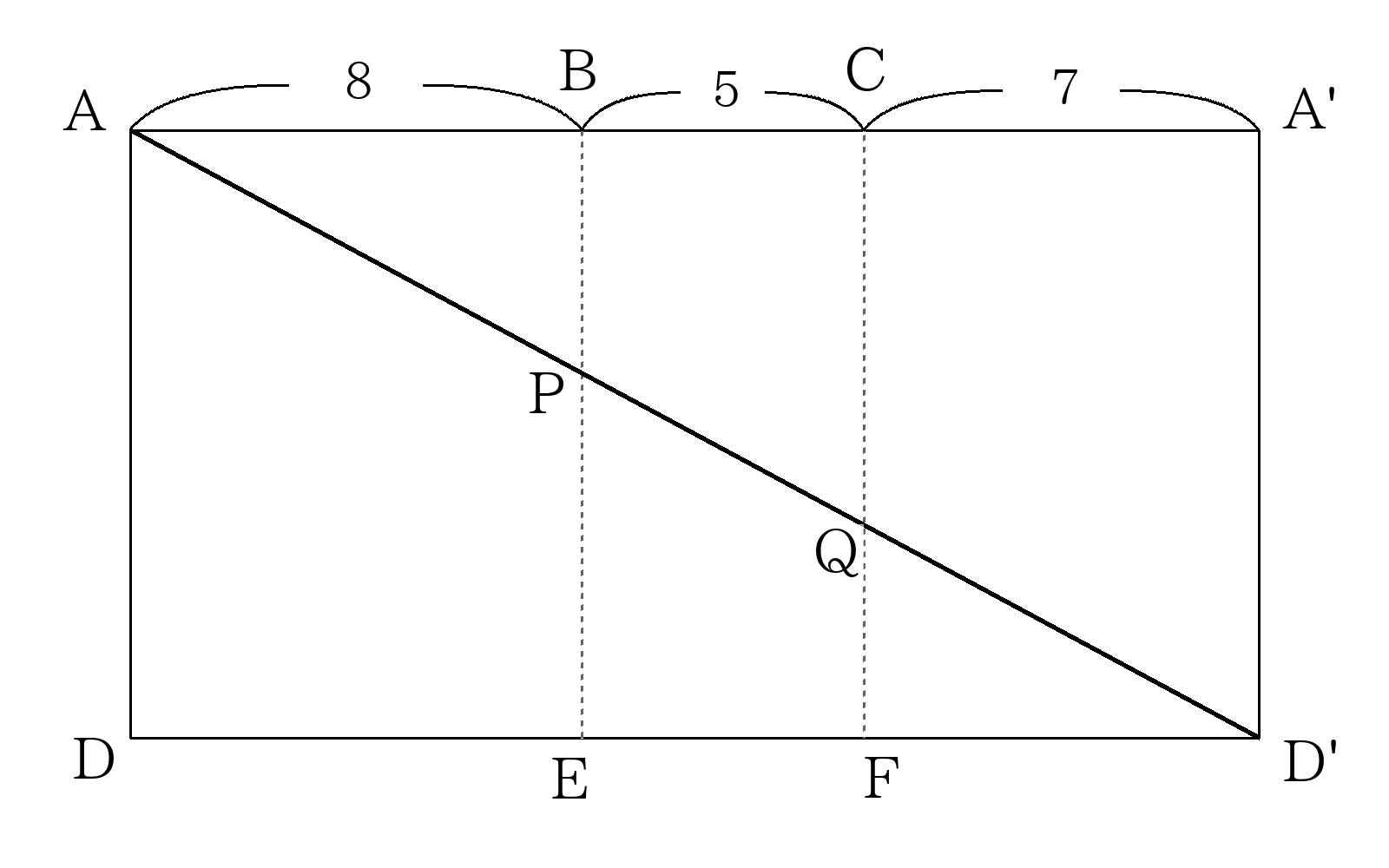
展開図を書き、点\(A\)と点\(D\)を直線で結ぶ。
三平方の定理より
\(AD’= \sqrt{(8+5+7)^2+8^2} \)
\(AD’=4 \sqrt{29} \)
\( \triangle D’QF \)∽\( \triangle D’PE \)∽\( \triangle D’AD \)の相似より
\(PQ=AD’ \times \dfrac{5}{8+5+7} \)
\(PQ=4 \sqrt{29} \times \dfrac{1}{4} \)
\(PQ= \sqrt{29} \)

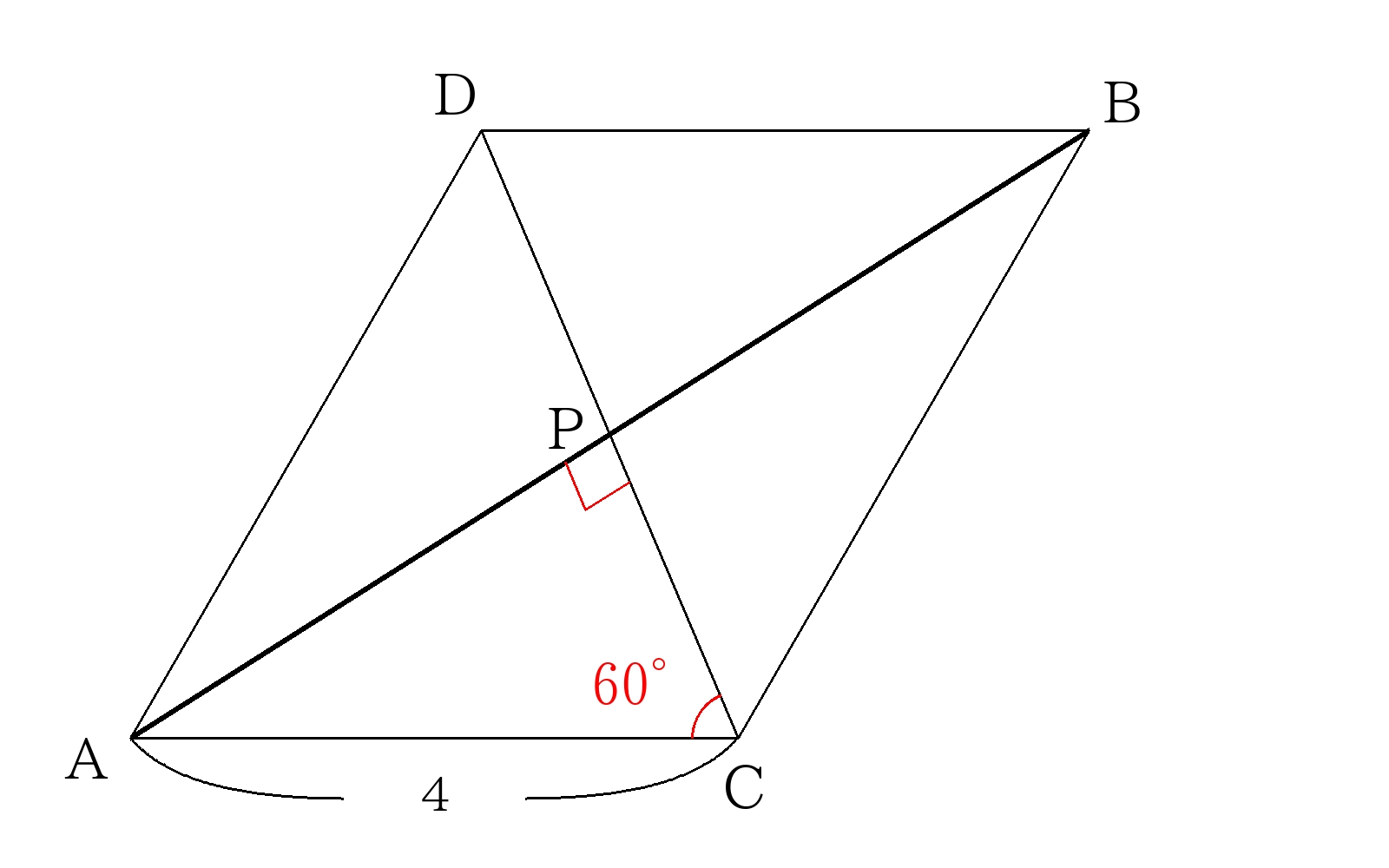
展開図を書き、点\(A\)と点\(B\)を直線で結ぶ。
\( \triangle ACP \)において三平方の定理より
\(AP=AC \times \dfrac{ \sqrt{3}}{2} \)
\(AP=2 \sqrt{3} \)
展開図を書く上で、中心角を計算する。
円錐の展開図において、\( \dfrac{半径}{母線}= \dfrac{中心角}{360}\)が成り立つので、
\( \dfrac{6}{18}= \dfrac{中心角}{360} \)
\(中心角=120 \)
ここで展開図を書いて図示する。なお、側面を2周するときは側面の展開図を2枚並べて書く。
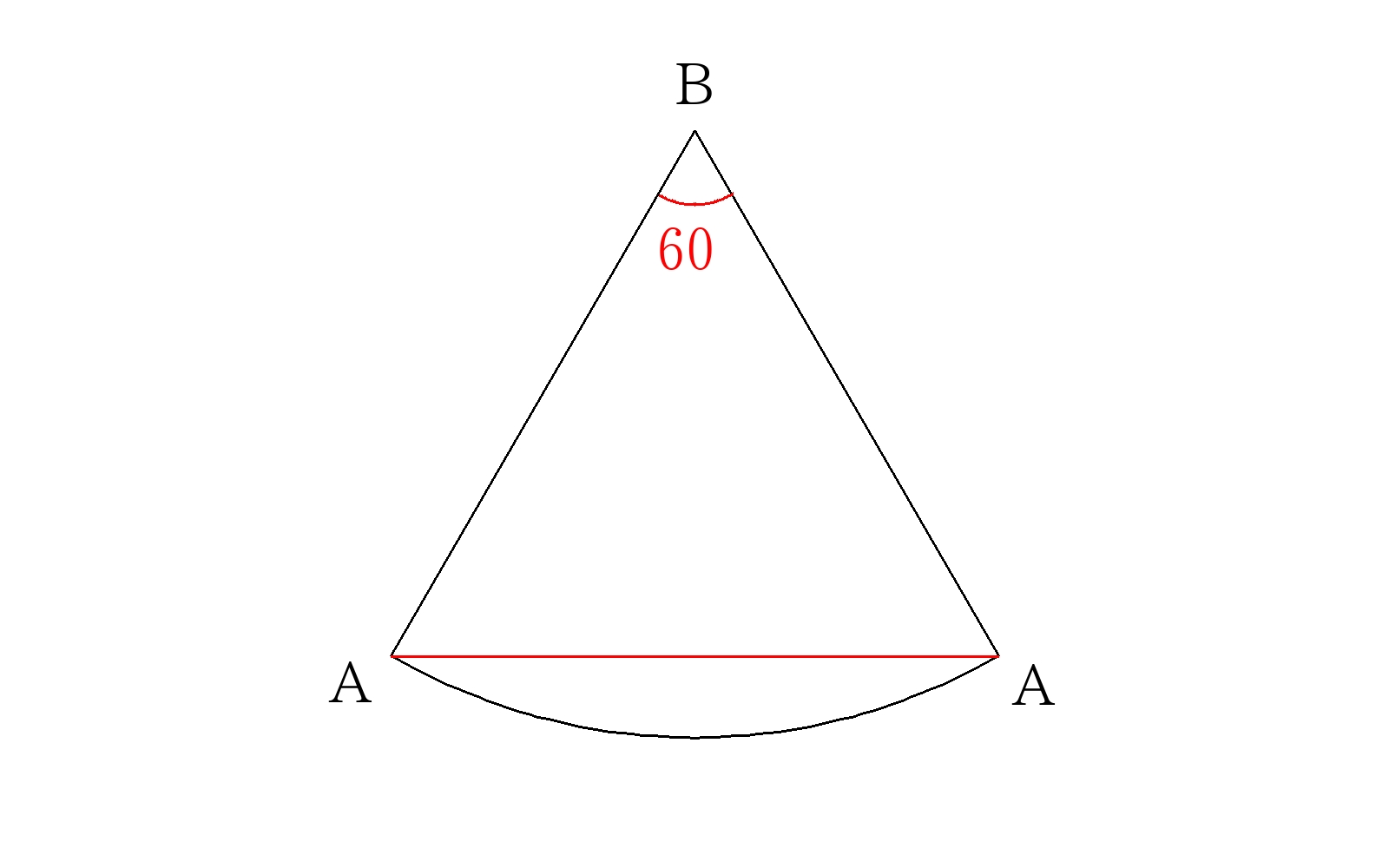
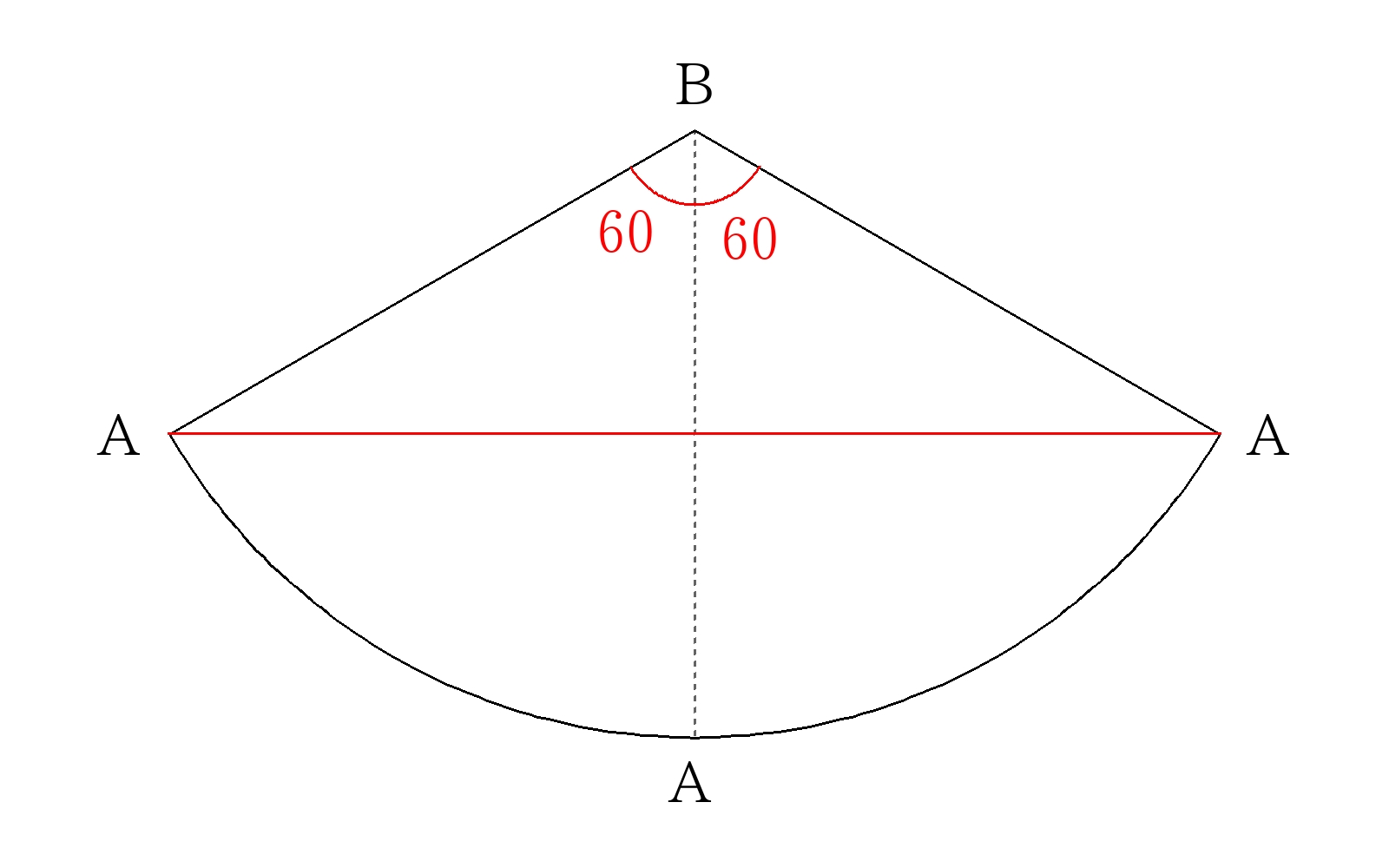
1周したときのひもの長さ\(L\)は正三角形を利用して、\(L=36\)
2周したときのひもの長さ\(M\)は30度60度の直角三角形を利用して、\(M=36 \sqrt{3}\)
\(L=36,M=36 \sqrt{3} \)
展開図を書く上で、中心角を計算する。
円錐の展開図において、\( \dfrac{半径}{母線}= \dfrac{中心角}{360}\)が成り立つので、
\( \dfrac{6}{18}= \dfrac{中心角}{360} \)
\(中心角=120 \)
ここで展開図を書いて図示する。なお、側面を2周するときは側面の展開図を2枚並べて書く。
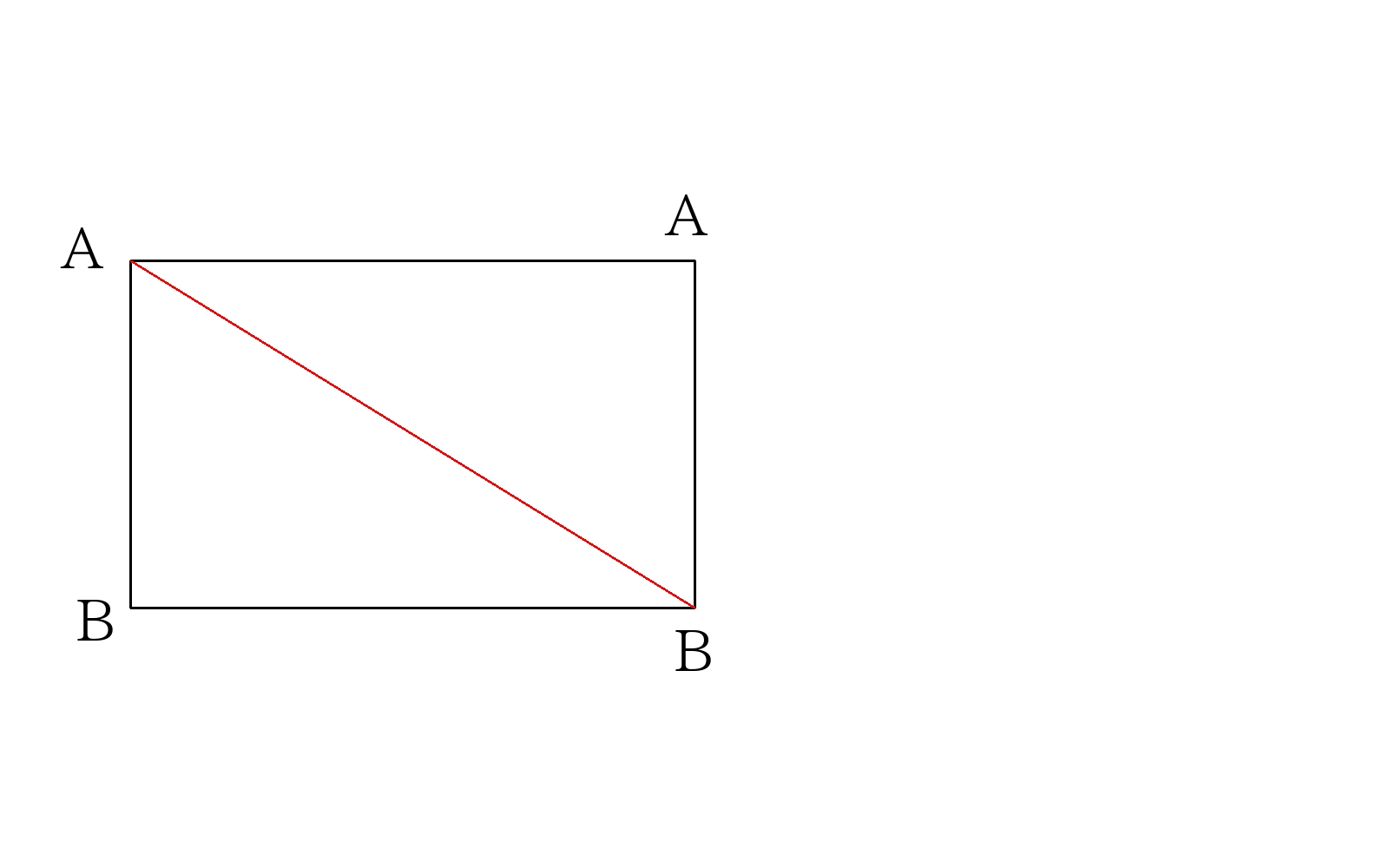
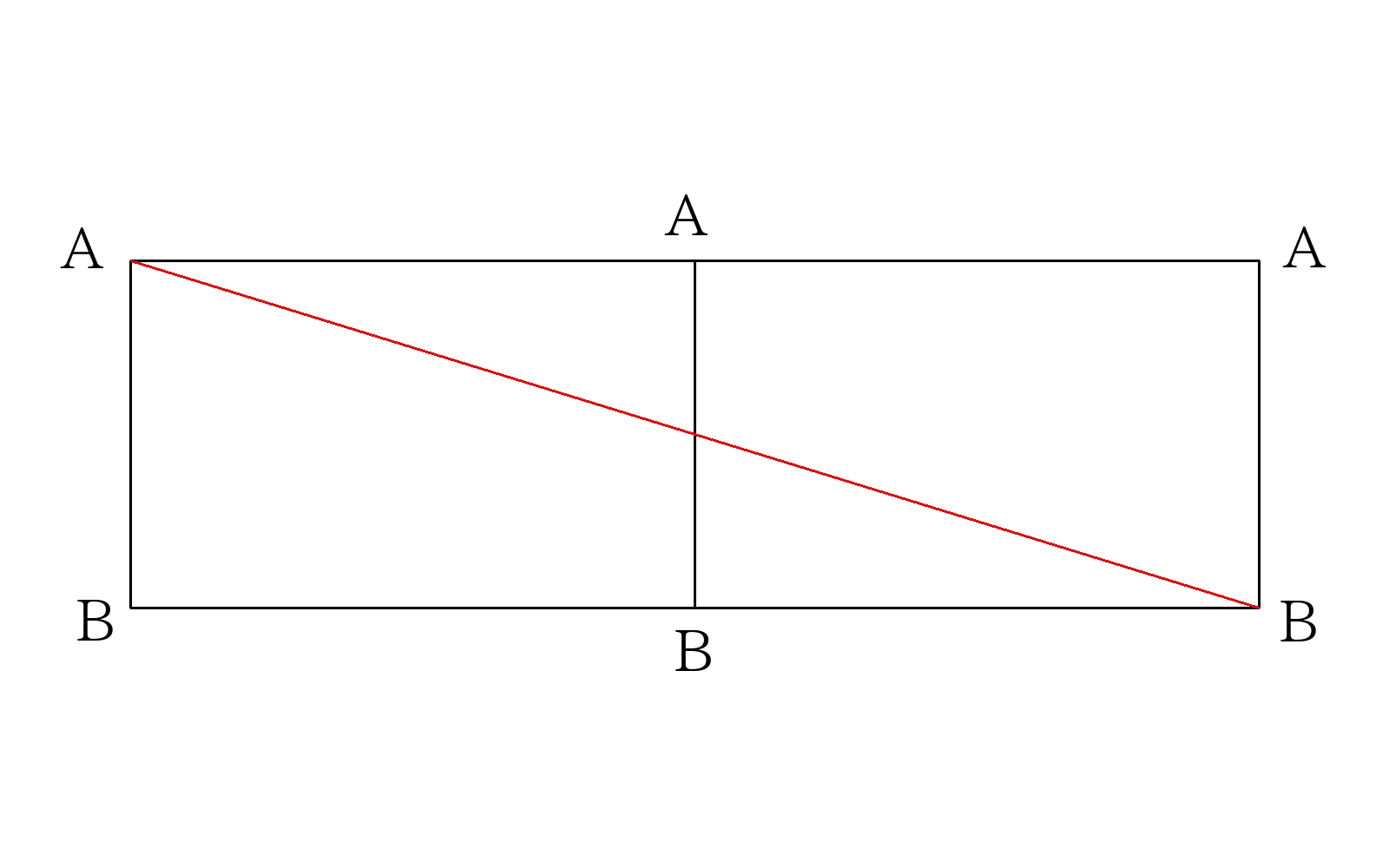
1周したときのひもの長さ\(L\)は三平方の定理より
\(L= \sqrt{12^2+18^2}=6 \sqrt{13} \)
2周したときのひもの長さ\(M\)は三平方の定理より
\(M= \sqrt{12^2+(18+18)^2}=12 \sqrt{10} \)
\(L=6 \sqrt{13},M=12 \sqrt{10} \)



コメント