速さの問題
- 2地点\(P\),\(Q\)があり、\(A\)君は\(P\)地を、\(B\)君は\(A\)君と同時に\(Q\)地を出発してそれぞれ\(PQ\)間を往復する。
\(A\)君が\(B\)君より時速\(3\)km速く進むと、2人が1回目に出会ってから2回目に出会うまで\(48\)分かかり、2回目に出会った地点は\(A\)から\(960m\)離れていた。\(A\)君の進む速さ、\(PQ\)間の距離をそれぞれ求めなさい。
- ダイヤグラムを書いて解く!
速さの原則は「ダイヤグラム」・・・
線分図のような状況図を書くぐらいならばダイヤグラムを書くこと。一方で速さの問題がすべてダイヤグラムで処理できるとは思わないこと。
ダイヤグラムで計算できる形を覚えて置くこと。
①進んだ距離の合計がわかる形(出会い)
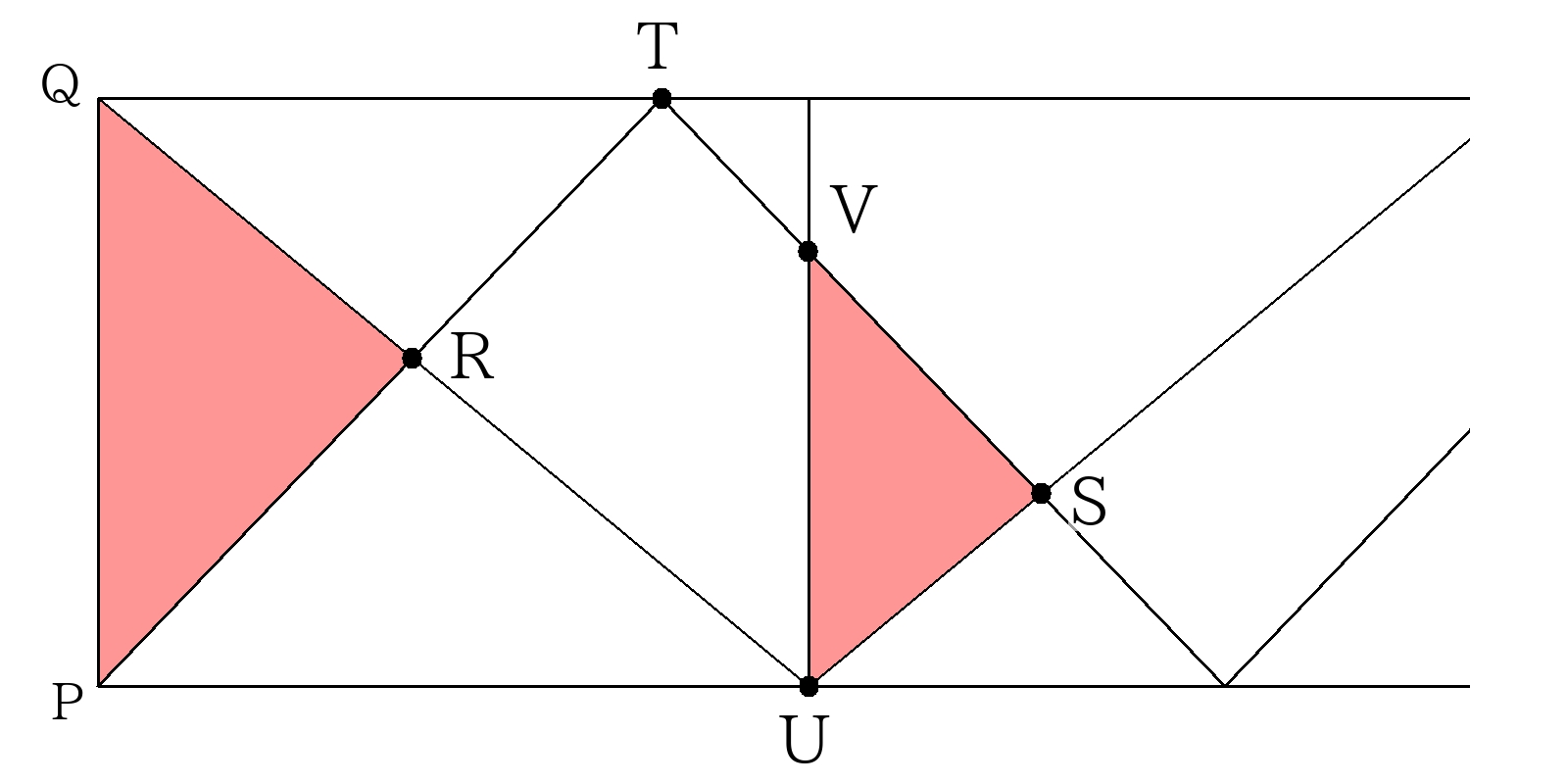
\( (PQの距離)+(QRの距離)=(PQの距離) \)
\( (USの距離)+(VSの距離)=(UVの距離) \)
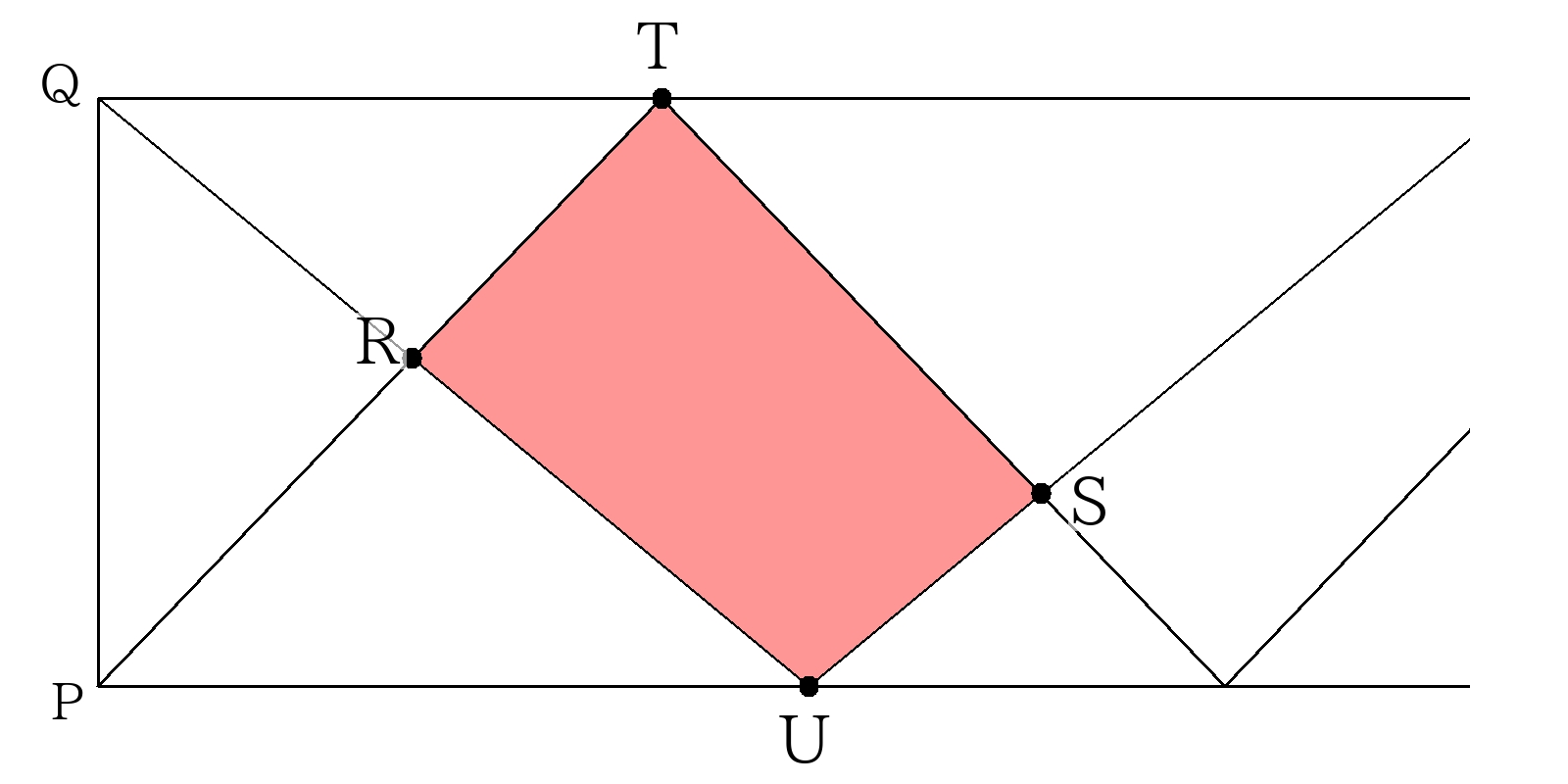
\( (RTの距離)+(RUの距離)\)
\(+(TSの距離)+(USの距離)\)\(=(PQの距離) \times 2 \)
※\( (RTの距離)+(RUの距離)=(PQの距離) \)
\( (TSの距離)+(USの距離)=(PQの距離) \)がそれぞれ成り立つ。
②進んだ距離の差がわかる形(追いつき)
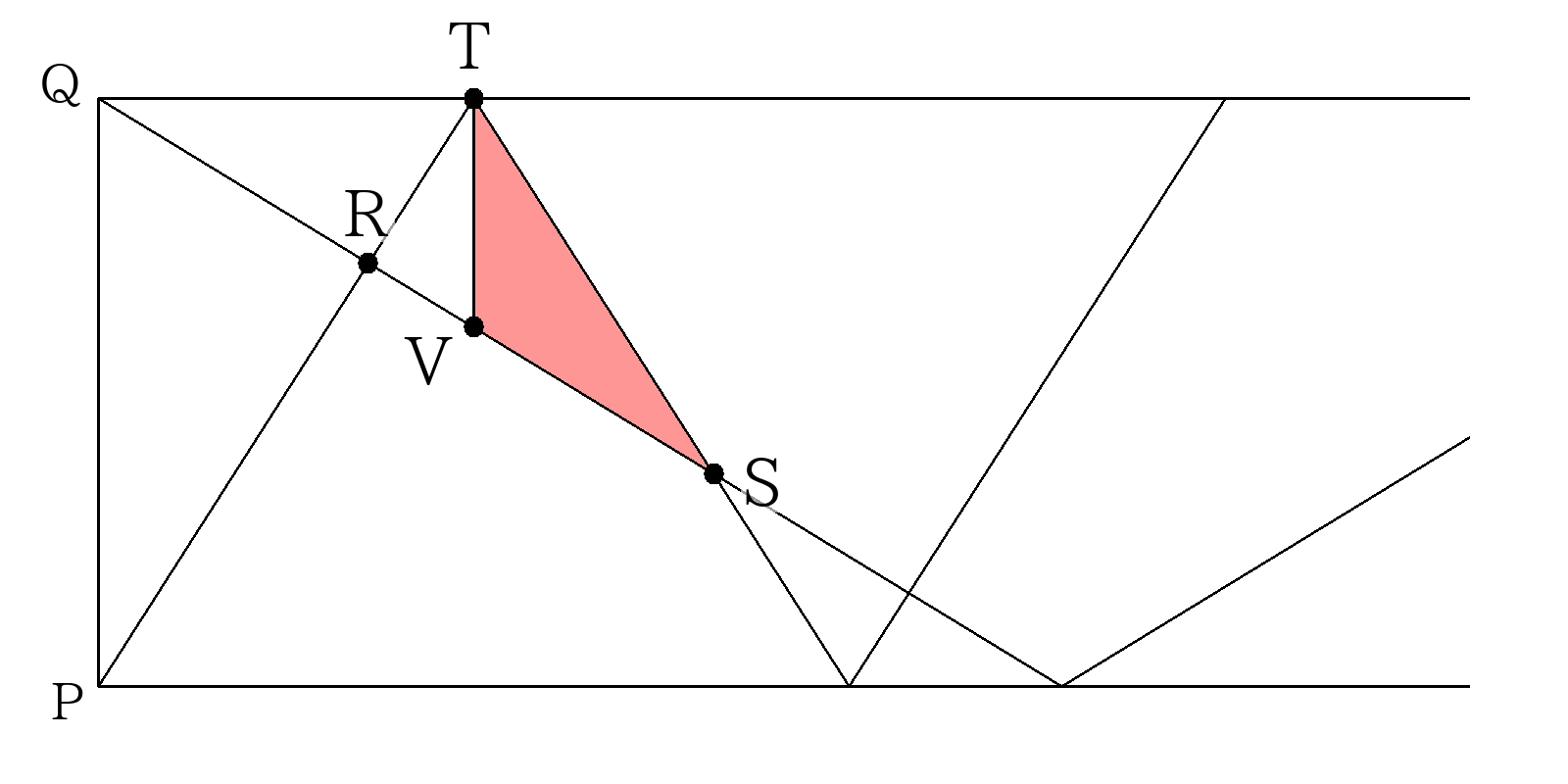
\( (TSの距離)-(VSの距離)=(TVの距離) \)
③相似形が使える形
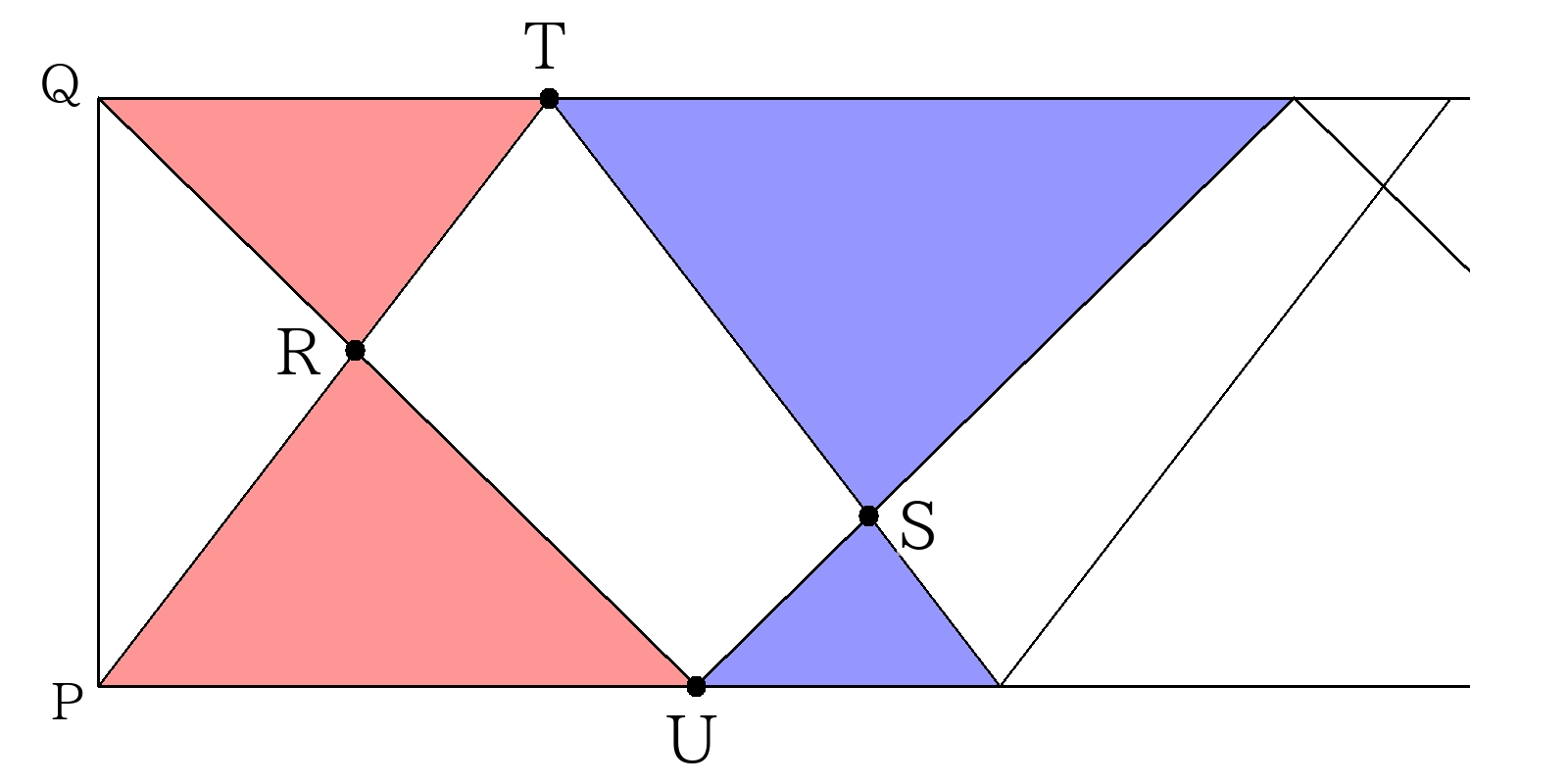
- 2地点\(P\),\(Q\)があり、\(A\)君は\(P\)地を、\(B\)君は\(A\)君と同時に\(Q\)地を出発してそれぞれ\(PQ\)間を往復する。
\(A\)君が\(B\)君より時速\(3\)km速く進むと、2人が1回目に出会ってから2回目に出会うまで\(48\)分かかり、2回目に出会った地点は\(A\)から\(960m\)離れていた。\(A\)君の進む速さ、\(PQ\)間の距離をそれぞれ求めなさい。
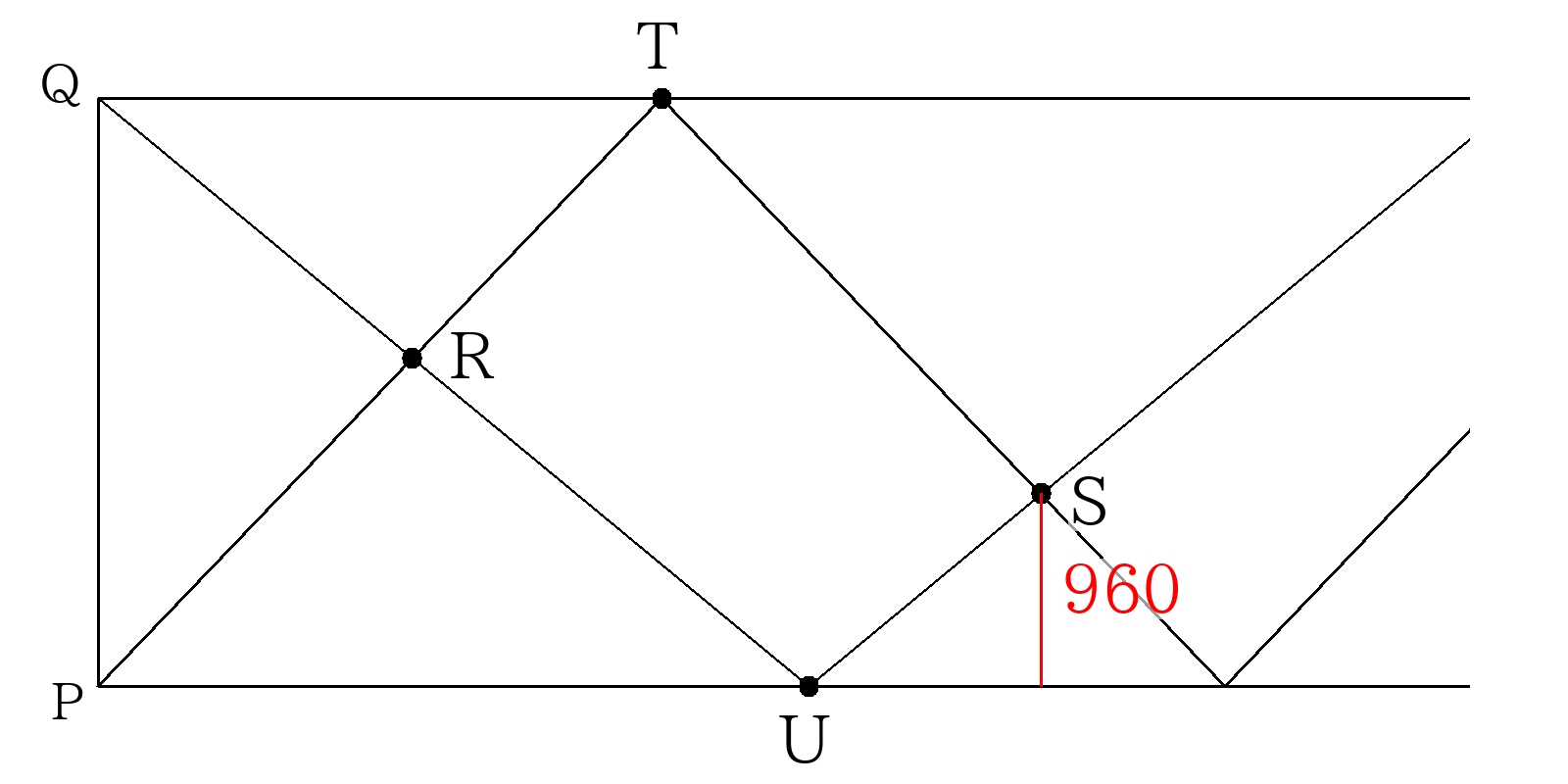
出発から1回目に出会うまでに2人が進んだ距離の合計\((PR+QR)\)は\(PQ間\)×1の距離
1回目から2回目に出会うまでに2人が進んだ距離の合計\((RT+TS+RU+US)\)は\(PQ間\)×2の距離
進んだ距離が2倍なのでかかる時間も2倍になる。
よって1回目に出会うまでの時間は
\(48 \div2=24分 \)
ここで、\(A\)君の速さを時速\(x\)kmとすると\(B\)君の速さは時速\((x-3)\)kmであり
1回目の出会いの条件より、
\( \dfrac{24}{60}x+ \dfrac{24}{60}(x-3)=AB \dots① \)
2回目の出会いまでに\(A\)君が進んだ条件より
\( \dfrac{48}{60}x=AB \times 2-0.96 \dots② \)
①,②より\(AB\)を消去するように計算すると、
\(0.8x=(0.8x-1.2) \times 2-0.96 \)
\(0.8x=1.6x-2.4-0.96 \)
\(0.8x=3.36 \)
\(x=4.2 \)
また①の式より
\(AB=2.16km \)
\(時速4.2km、2.16km \)



コメント