比を合わせる
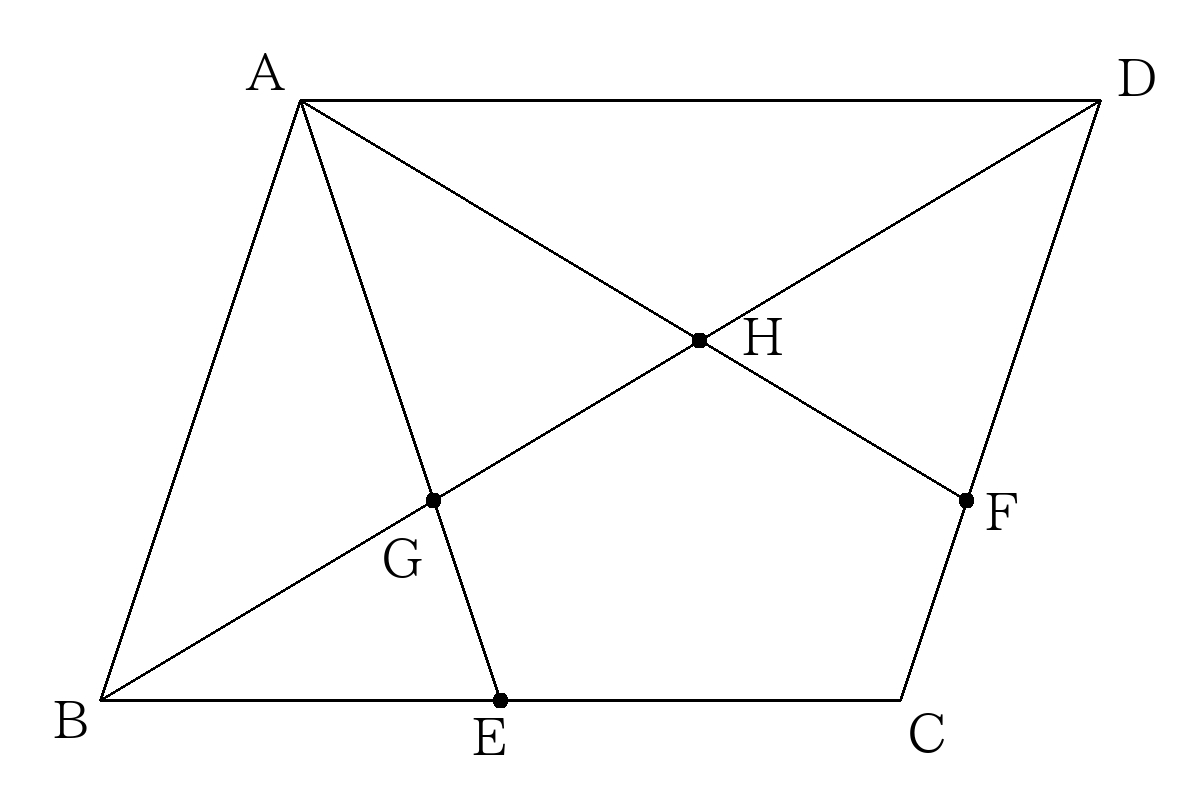
- 次の図のような平行四辺形\(ABCD\)があり、\(BE:EC=1:1\)、\(DF:FC=2:1\)である。このとき\(BG:GH:HD\)を求めなさい。
- ①の問題において、\( \triangle AGH\)の面積は平行四辺形\(ABCD\)の何倍か。
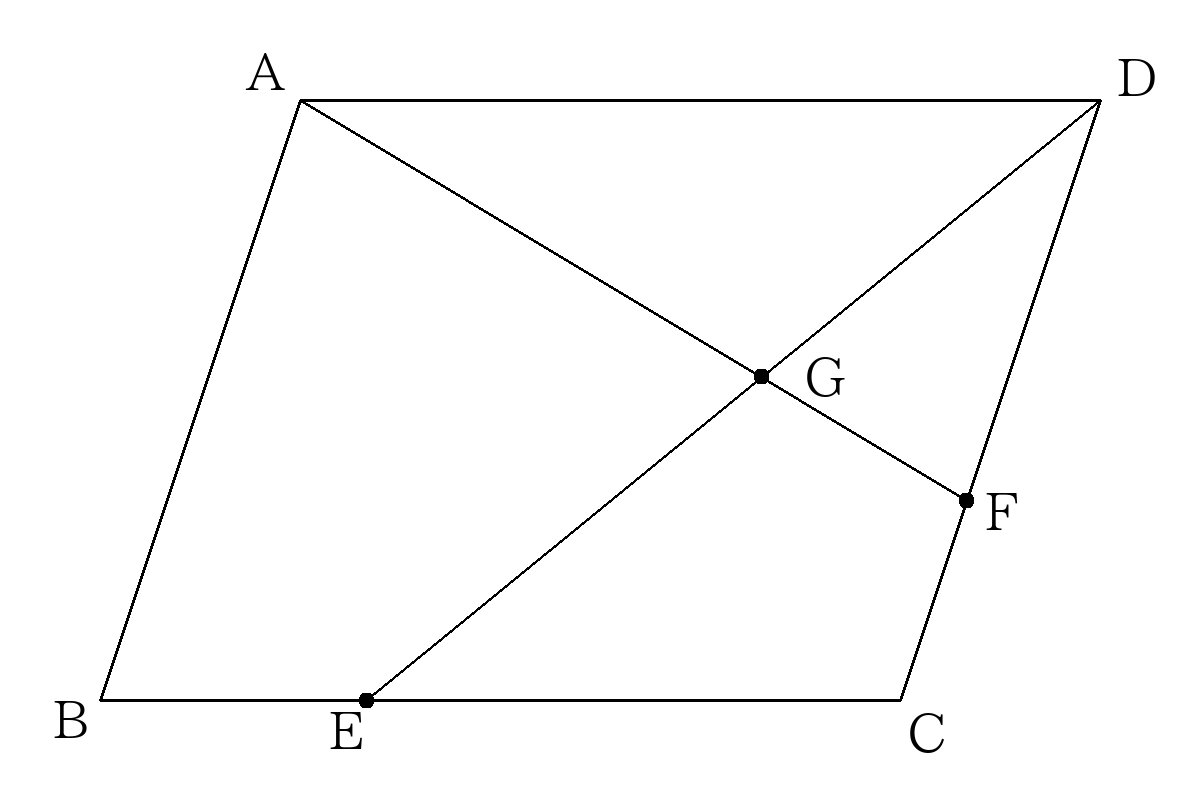
- 次の図のような平行四辺形\(ABCD\)があり、\(BE:EC=2:1\)、\(DF:FC=2:1\)である。\( \triangle ADG\)の面積は平行四辺形\(ABCD\)の何倍か。
- 相似な図形を見つける、つくる。
- 比を割合で合わせる。
- 面積は「底辺」と「高さ」の比で求める。
※相似の図形の面積比や等高三角形の面積比から求める方法もあるが、今回は底辺と高さから求める方法にする。
面積が「たて」と「よこ」の長さの積であることを改めて実感してほしい。
相似の図形の作り方
・平行線
・つのだし
②比を割合で合わせる。
次の図で、\(AB:BD=1:2\)、\(AC:CD=4:3\)のとき\(AB:BC:CD\)を求める。
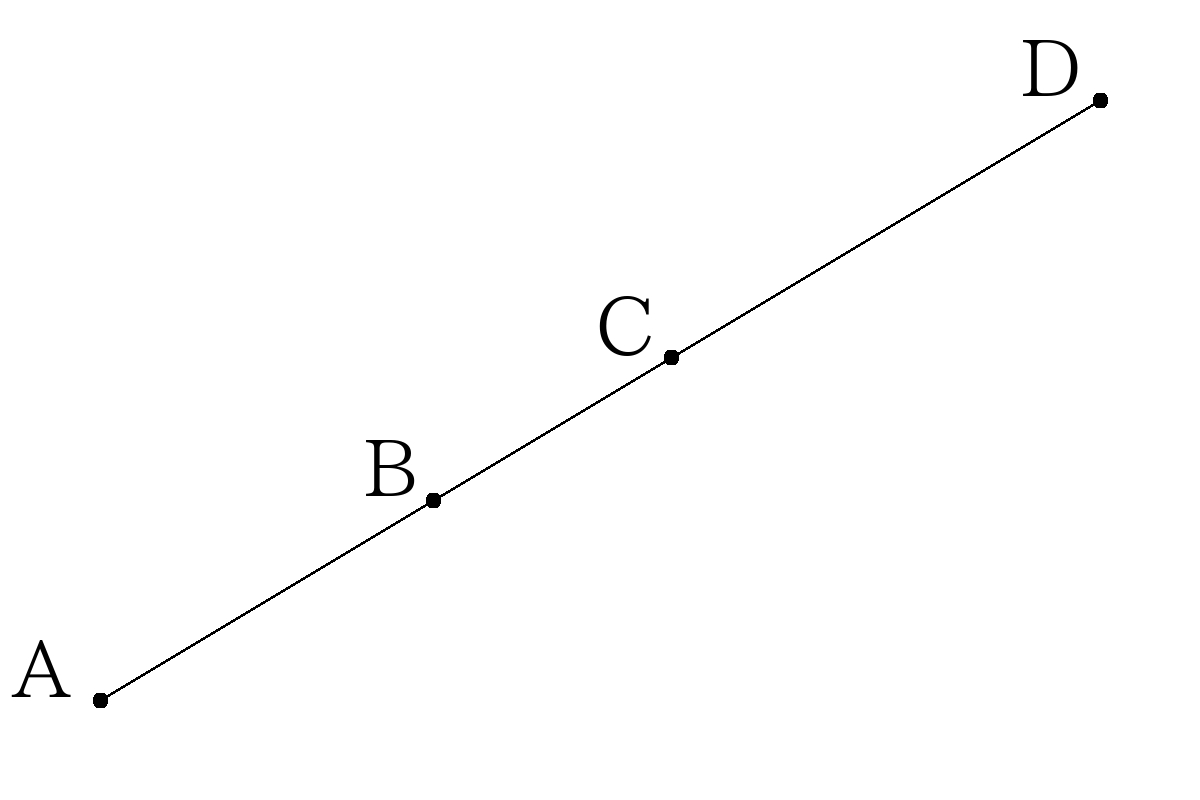
\(AD\)の長さと比べると、
\(AB=\dfrac{1}{1+2}AD=\dfrac{1}{3}AD\)、\(BD=\dfrac{2}{1+2}AD=\dfrac{2}{3}AD\)
\(AC=\dfrac{4}{4+3}AD=\dfrac{4}{7}AD\)、\(CD=\dfrac{3}{4+3}AD=\dfrac{3}{7}AD\)
また、\(BC=AC-AB=\dfrac{4}{7}AD-\dfrac{1}{3}AD=\dfrac{5}{21}AD\)
よって、\(AB:BC:CD=\dfrac{1}{3}AD:\dfrac{5}{21}AD:\dfrac{3}{7}AD=7:5:9\)
③高さ(の比)をとらえる
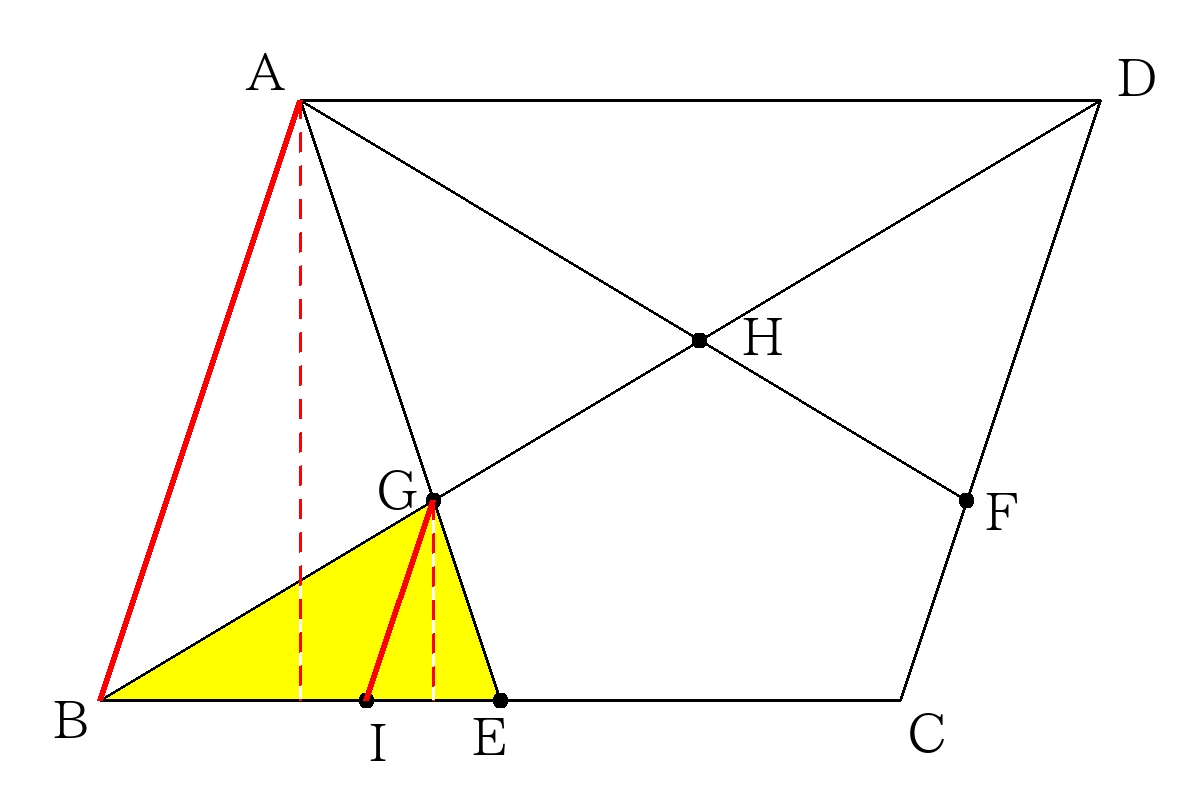
\(\triangle BGE\)の高さと平行四辺形の高さの比は\(GI:AB\)で決まる。
本来は、点\(A\)、点\(G\)から\(BC\)に垂直な線が高さであるが、
\(GI /\!/ AB\)で相似の関係より、\(GI:AB\)が高さの比となる。
※角度が等しかったり(平行であったり)、補角(和が180°)の関係であったりする場合、高さの比を出すことを考えること。
- 次の図のような平行四辺形\(ABCD\)があり、\(BE:EC=1:1\)、\(DF:FC=2:1\)である。このとき\(BG:GH:HD\)を求めなさい。
- ①の問題において、\( \triangle AGH\)の面積は平行四辺形\(ABCD\)の何倍か。
- 次の図のような平行四辺形\(ABCD\)があり、\(BE:EC=2:1\)、\(DF:FC=2:1\)である。\( \triangle ADG\)の面積は平行四辺形\(ABCD\)の何倍か。
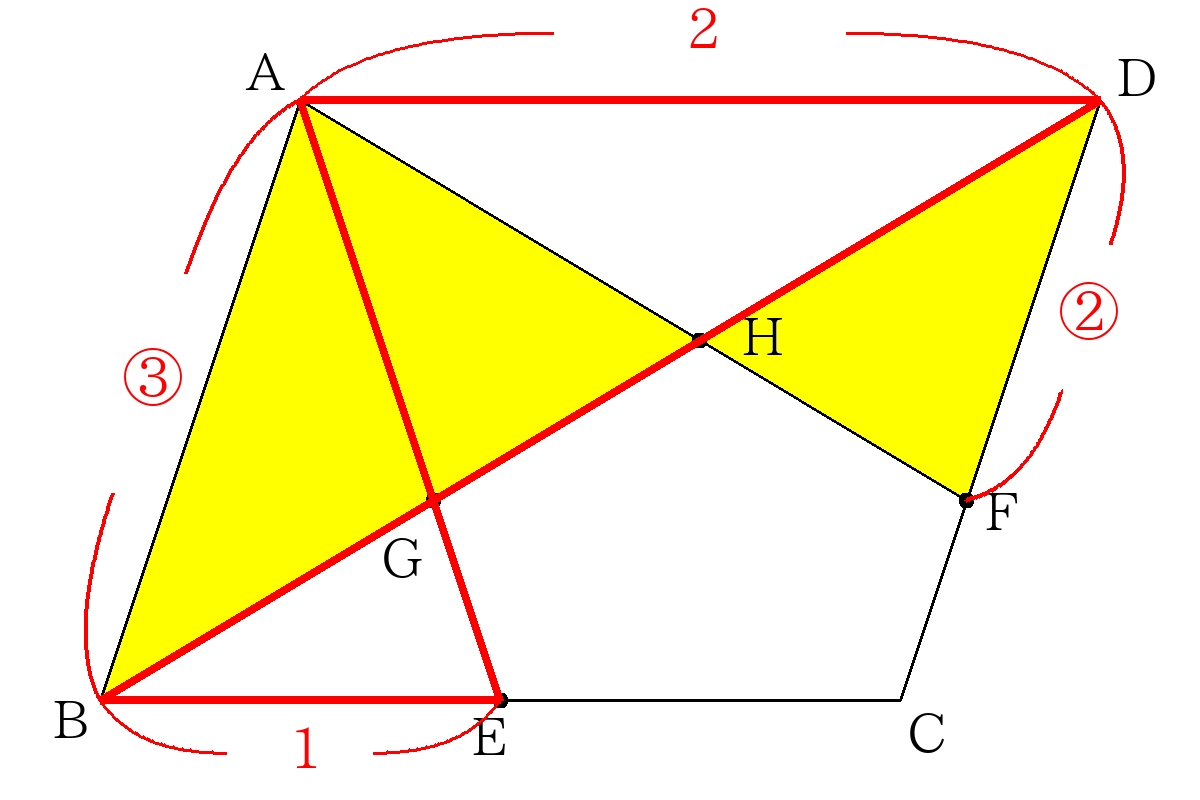
\(BG= \dfrac{1}{1+2}BD= \dfrac{1}{3}BD \)
\(GD= \dfrac{2}{1+2}BD= \dfrac{2}{3}BD \)
\(BH= \dfrac{3}{3+2}BD= \dfrac{3}{5}BD \)
\(HD= \dfrac{2}{3+2}BD= \dfrac{2}{5}BD \)
\(GH=BH-BG= \dfrac{3}{5}BD- \dfrac{1}{3}BD= \dfrac{4}{15}BD \)
\(BG:GH:HD=\dfrac{1}{3}BD:\dfrac{4}{15}BD:\dfrac{2}{5}BD\)
\(=\dfrac{5}{15}BD:\dfrac{4}{15}BD:\dfrac{6}{15}BD\)より
\(BG:GH:HD=5:4:6 \)
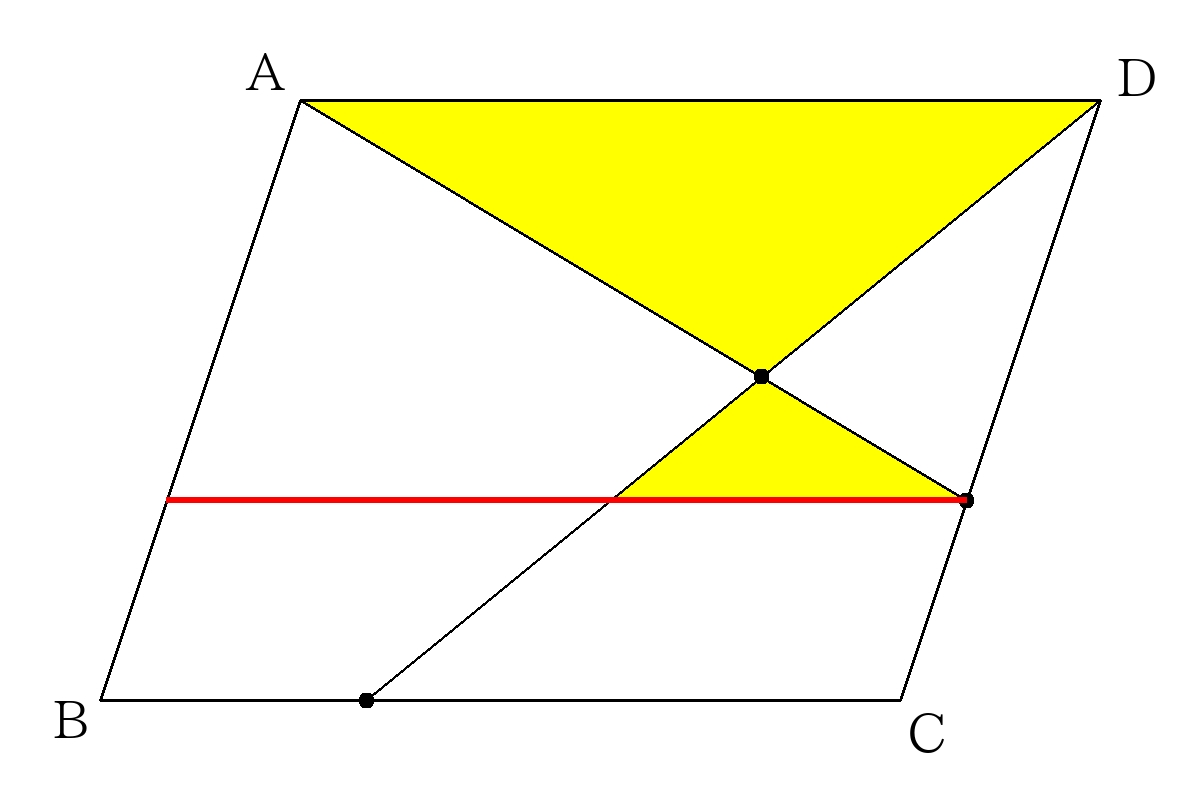
\(\triangle AGH\)は、\(\triangle ABD\)と高さが等しいため、底辺の比によって面積がきまる。
\(\triangle ABD=\dfrac{1}{2}ABCD\)より
\( \triangle AGH= \dfrac{5}{5+4+6} \times \triangle ABD \)
\(= \dfrac{1}{3} \times \dfrac{1}{2}□ABCD \)
\(= \dfrac{1}{6}□ABCD \)
\( \dfrac{1}{6}倍 \)
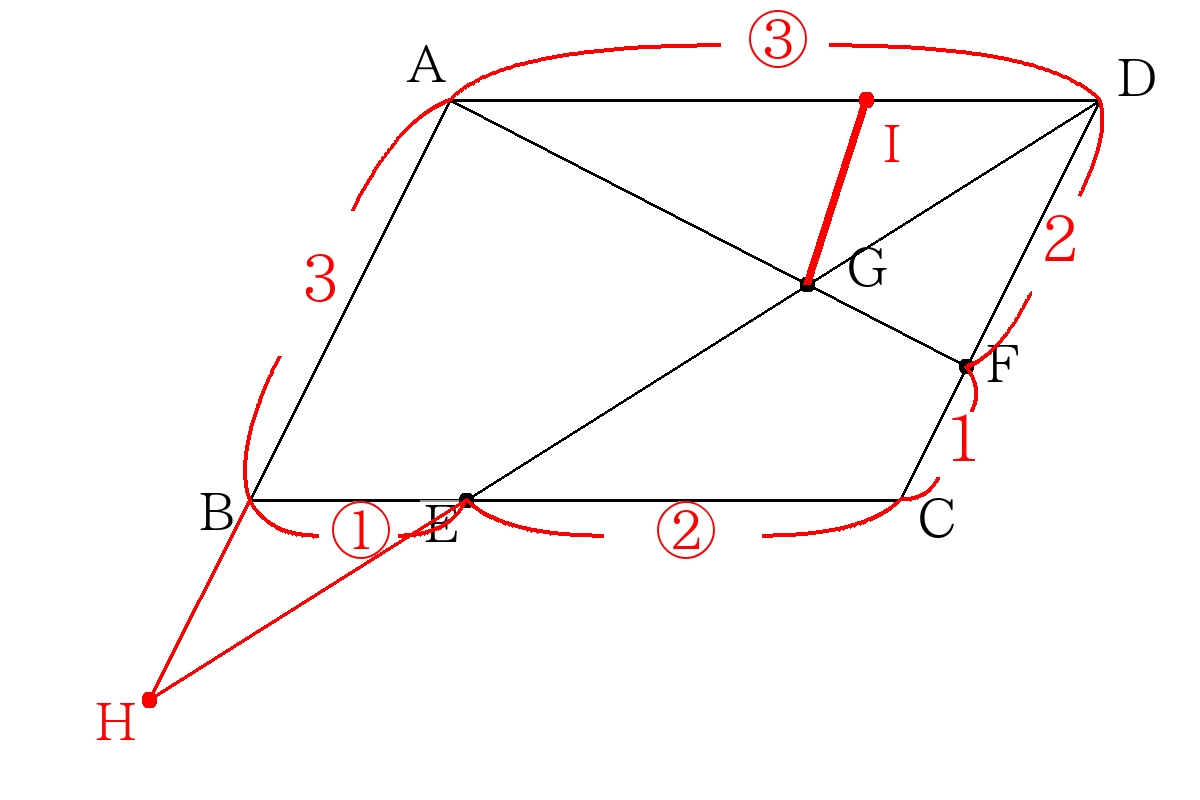
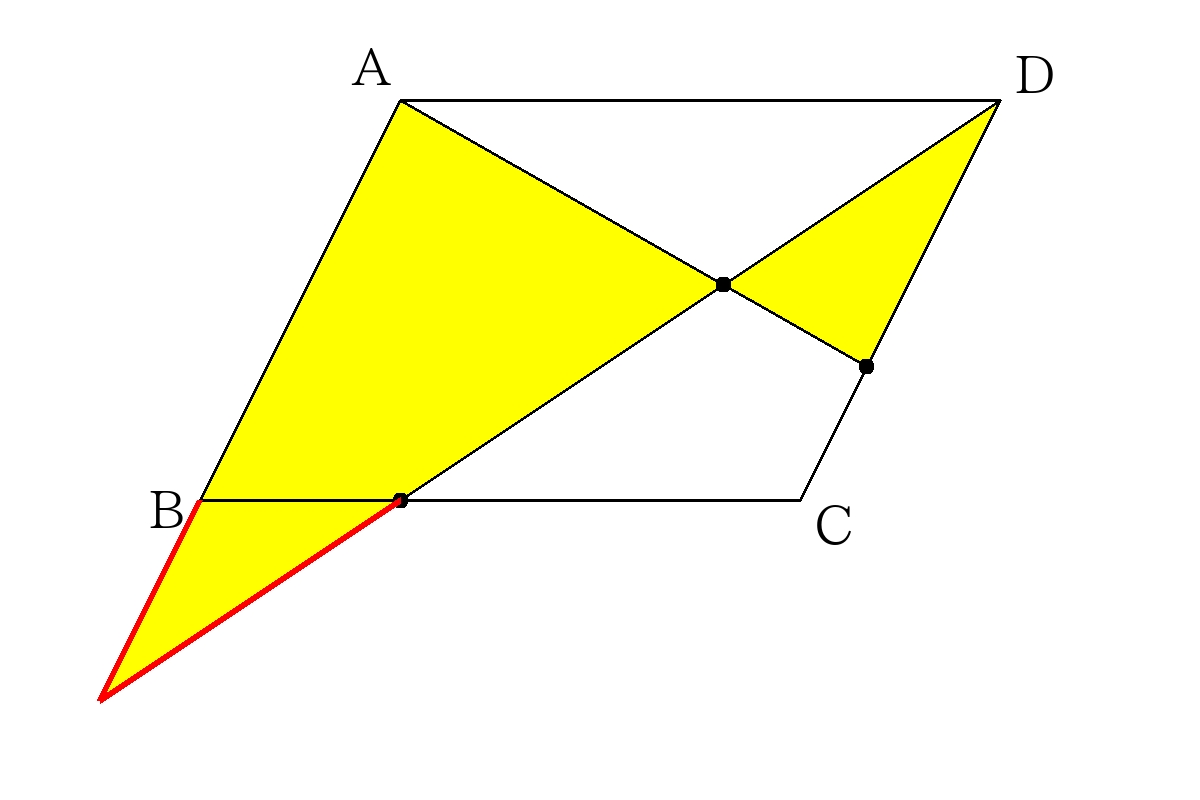
\(AB\)の延長線と\(DE\)の延長線との交点を\(H\)とする。
\(HB:HA=1:3\)より
\(\triangle ADG\)の面積を求めるために、\(G\)を通り\(DC\)に平行な線を引き、\(AD\)との交点を\(I\)とする。
平行四辺形\(ABCD\)の面積と\( \triangle ADG\)の面積の比は
\((BC \times AB):\left(AD \times IG \times \dfrac{1}{2} \right) \)で求めるので
\((③ \times 3): \left(③ \times \dfrac{8}{13} \times \dfrac{1}{2} \right) \)
\(=39:16 \)
\( \dfrac{16}{39}倍 \)
※\(\triangle AGD \)の面積ならば\(\triangle AFD \)の底面の比から求める方が自然。\(\triangle GFD \)の面積を求めるときは高さを算出した方が解きやすい。複雑な図形ほど「高さを出す」ことを意識してほしい。



コメント