三角形の高さと面積
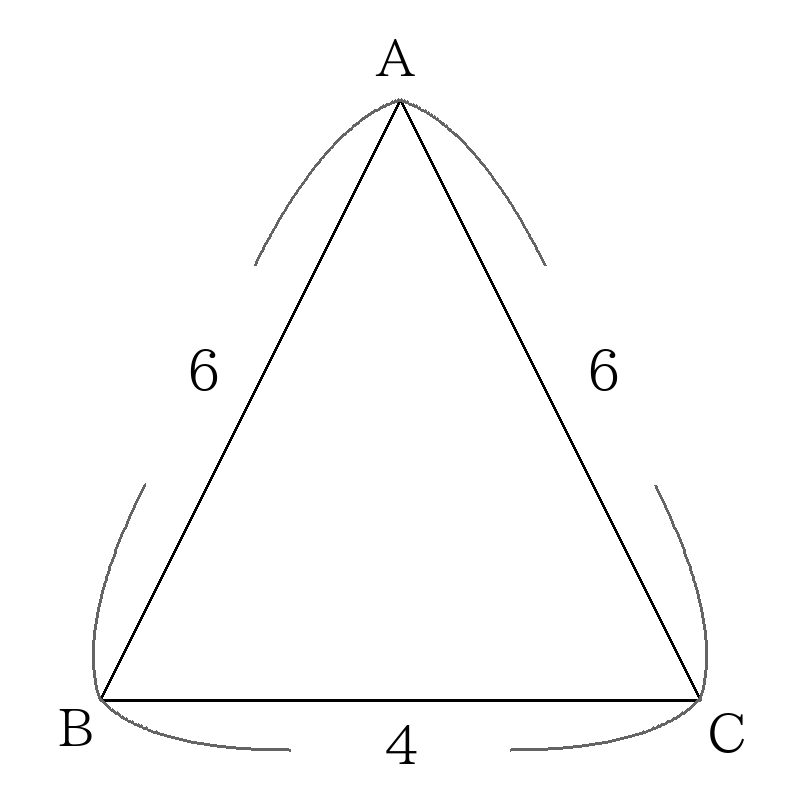
次の図の三角形\(ABC\)の面積を求めなさい。
- 二等辺三角形は頂点から底辺に垂線を下す。
- 特別角(30度、60度、45度)は積極的に使う。
- 三辺の長さが与えられたら、1つの頂点から底辺に垂線を下し、方程式に持ち込む。
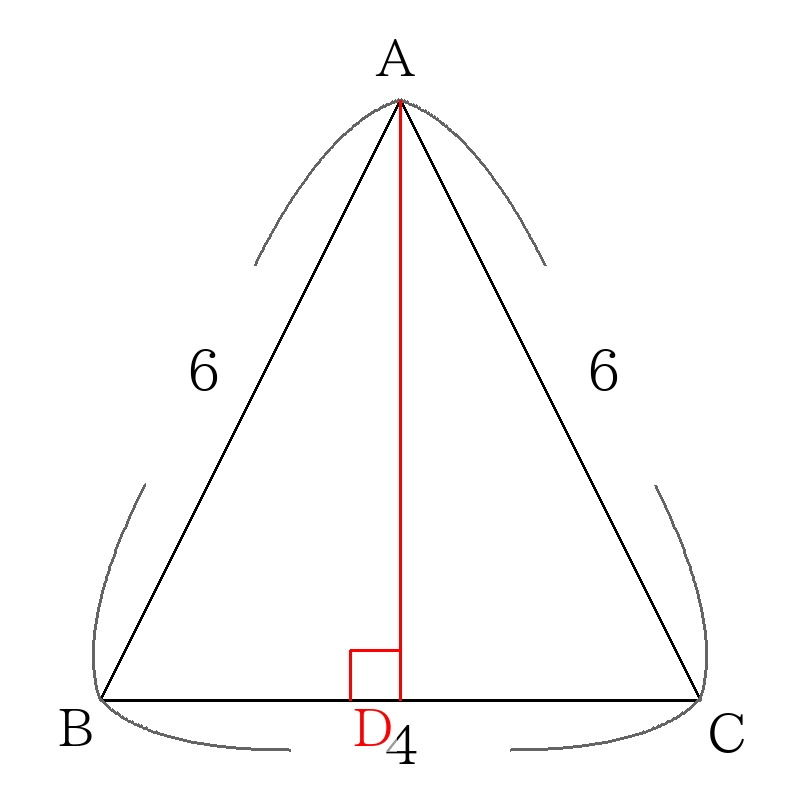
頂点\(A\)から辺\(BC\)に引いた垂線を\(AD\)とする。
二等辺三角形の頂点から底辺に引いた垂線は、底辺を二等分するので、
\(BD= \dfrac{1}{2}BC=2 \)
\(\triangle ABD\)において三平方の定理を用いると
\(AD^2=6^2-2^2 \)
\(AD=±4 \sqrt{2} \)
\(AD>0\)より
\(AD=4 \sqrt{2} \)
よって三角形\(ABC\)の面積は
\(4 \times 4 \sqrt{2} \times \dfrac{1}{2}=8 \sqrt{2} \)
\(8 \sqrt{2} \)
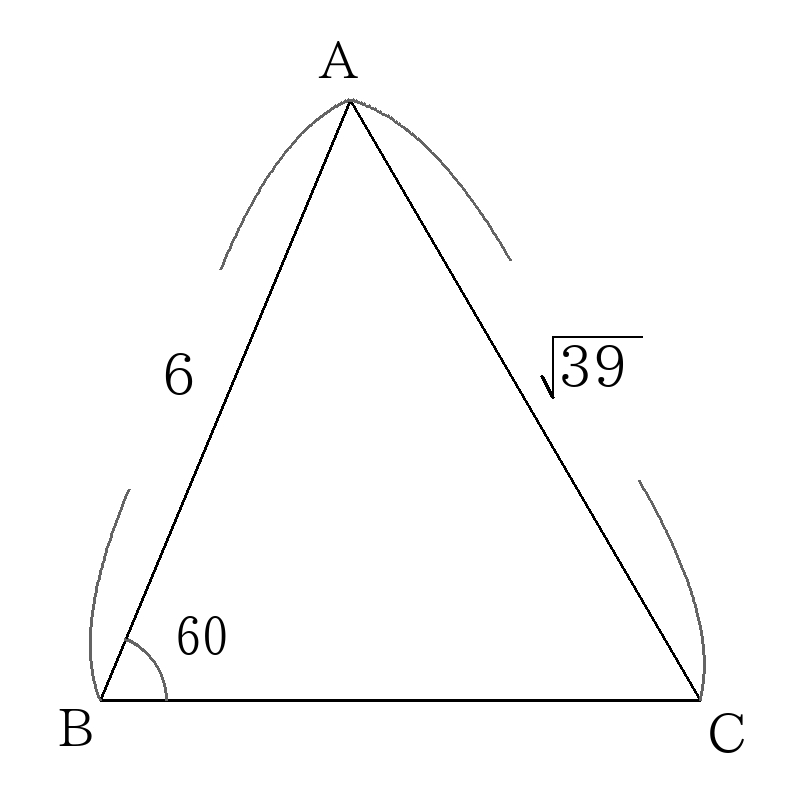
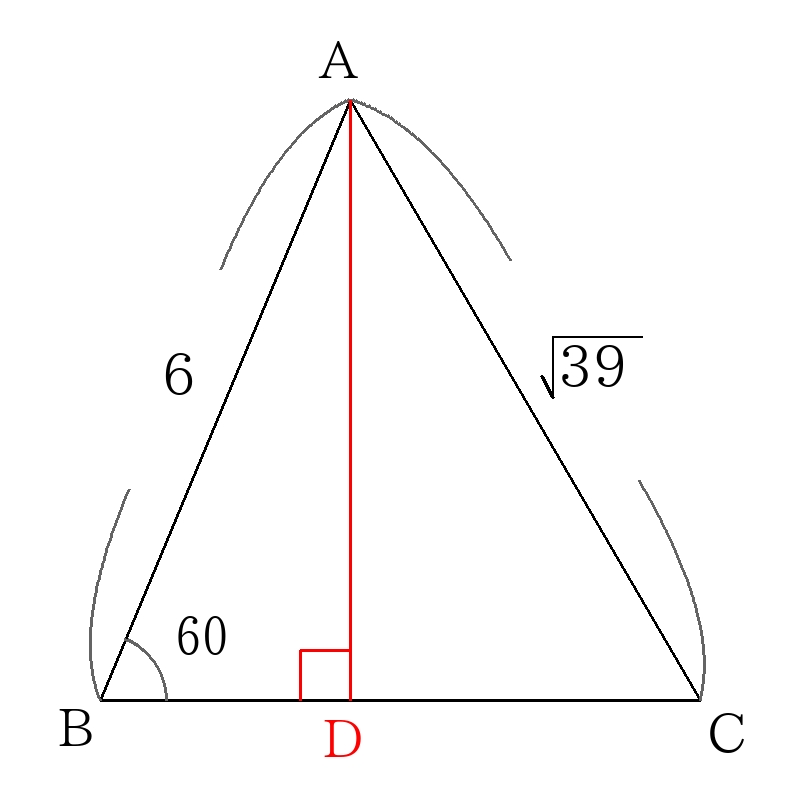
頂点\(A\)から辺\(BC\)に引いた垂線を\(AD\)とする。
\( \triangle ABD \)は30度、60度の直角三角形なので、\(1:2:\sqrt{3}\)の辺の比を用いると
\(BD=3,AD=3 \sqrt{3} \)
\(\triangle ADC\)において三平方の定理を用いると
\(DC^2= \left( \sqrt{39} \right)^2- \left(3 \sqrt{3} \right)^2 \)
\(DC=±6 \)
\(DC>0\)より
\(DC=6 \)
よって三角形\(ABC\)の面積は
\((3+6) \times 3 \sqrt{3} \times \dfrac{1}{2}= \dfrac{81}{2} \sqrt{3} \)
\( \dfrac{81}{2} \sqrt{3} \)
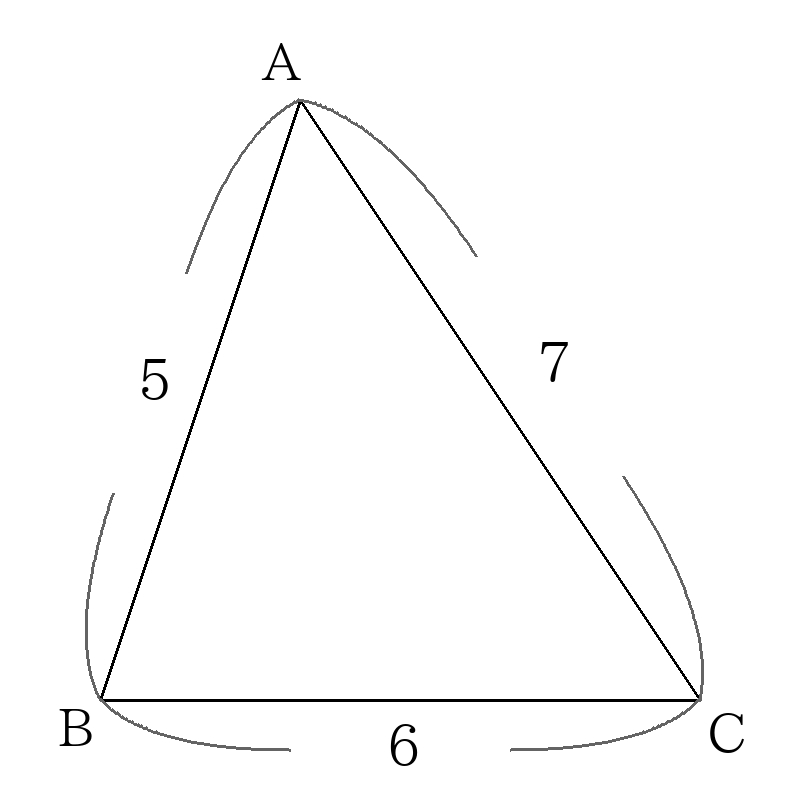
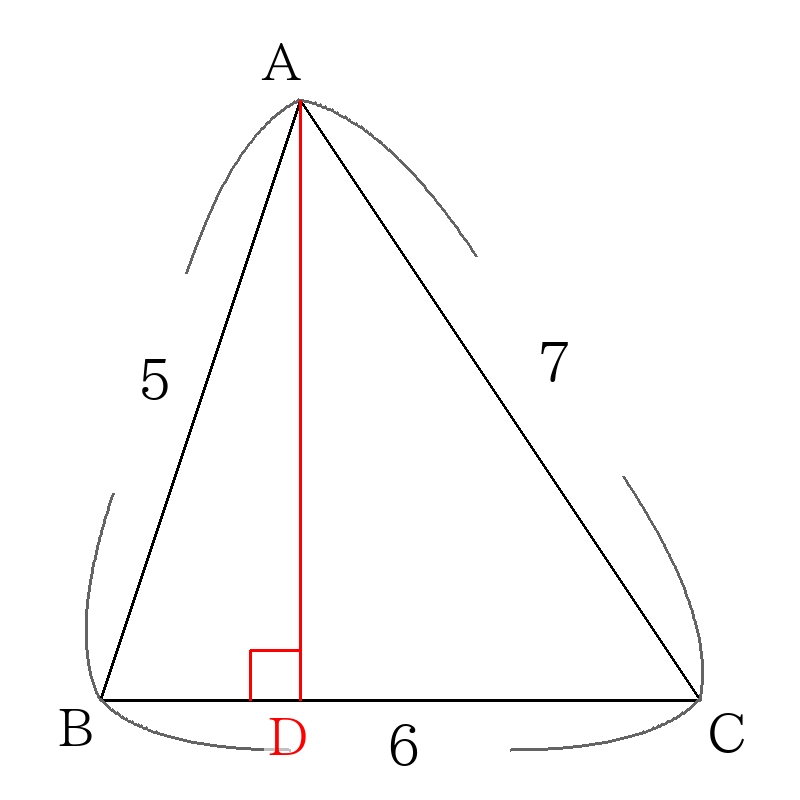
頂点\(A\)から辺\(BC\)に引いた垂線を\(AD\)とする。
\(BD=x\)とおき、\(\triangle ABD\)において三平方の定理を用いると
\(AD^2=5^2-x^2 \dots① \)
また、\(DC=6-x\)であり、\(\triangle ADC\)において三平方の定理を用いると
\(AD^2=7^2-(6-x)^2 \dots② \)
①、②より
\(5^2-x^2=7^2-(6-x)^2 \)
計算すると
\(x=1 \)
\(\triangle ABD\)において三平方の定理を用いると
\(AD^2=5^2-1^2 \)
\(AD>0\)より、
\(AD=2 \sqrt{6} \)
よって三角形\(ABC\)の面積は
\(6 \times 2 \sqrt{6} \times \dfrac{1}{2}=6 \sqrt{6} \)
\(6 \sqrt{6} \)



コメント