円
複数の内接円
例題
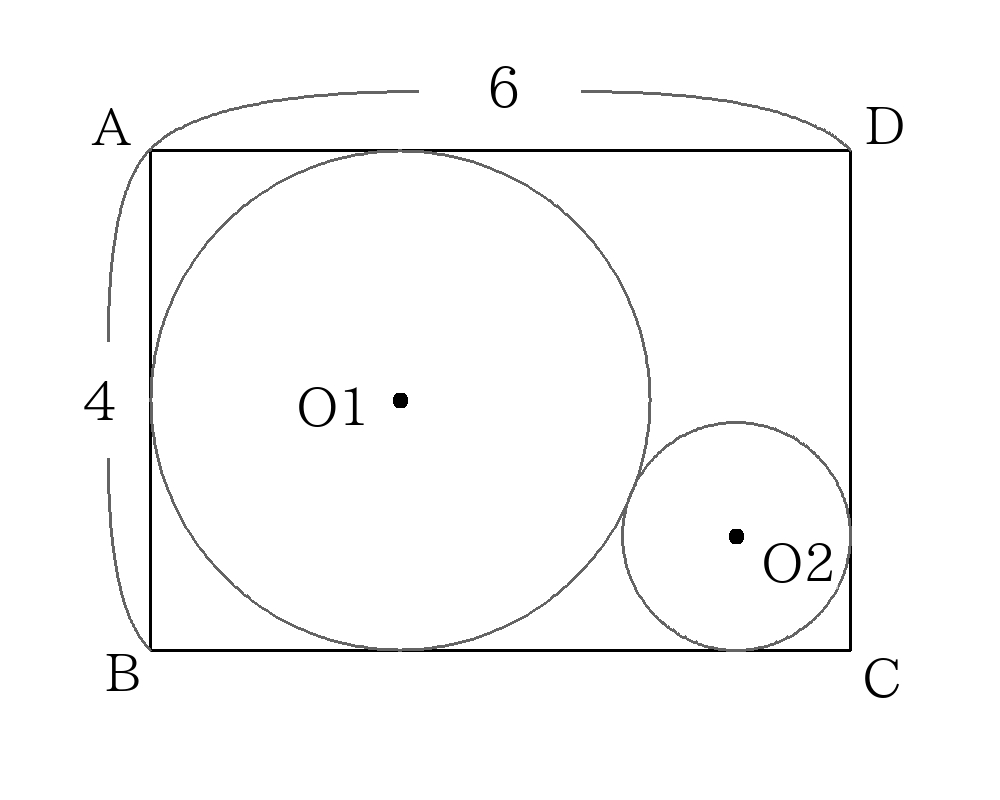
- 長方形\(ABCD\)があり、2つの円\(O1\)と\(O2\)が次の図のように内接している。このとき\(O2\)の半径を
求めなさい。
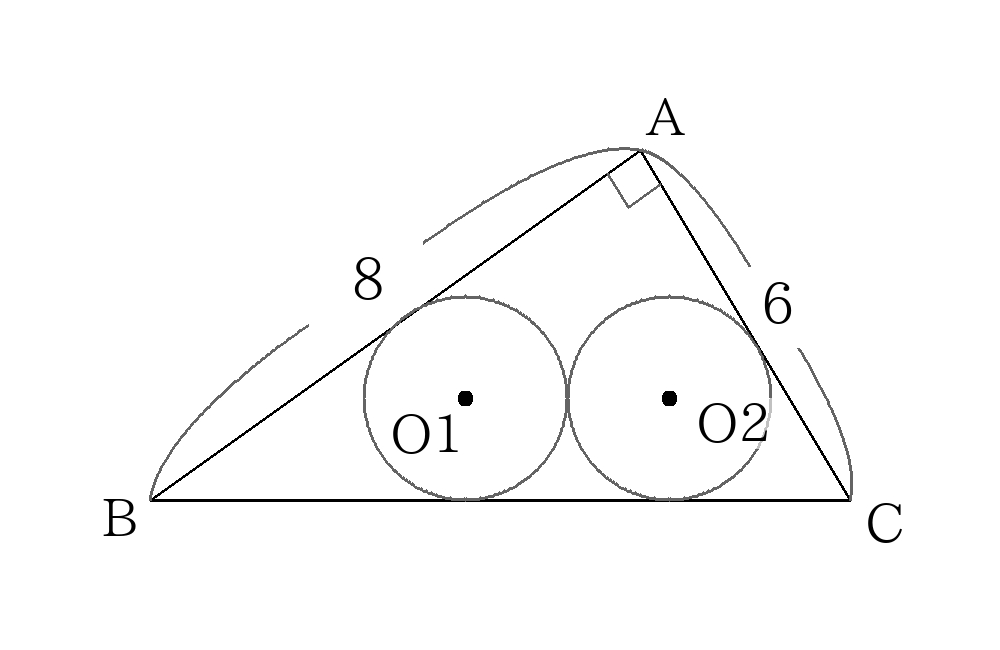
- 直角三角形\(ABC\)に半径が等しい2つの円\(O1\)と\(O2\)が次の図のように内接している。このとき\(O1\)、\(O2\)の半径を求めなさい。
まずはこう解け!
- 円の中心、接点を結ぶ
- 内接円が1つのときと比べて、相似を利用する。※詳細は下記参照
内接円が1つのときと比べて、相似を利用する。
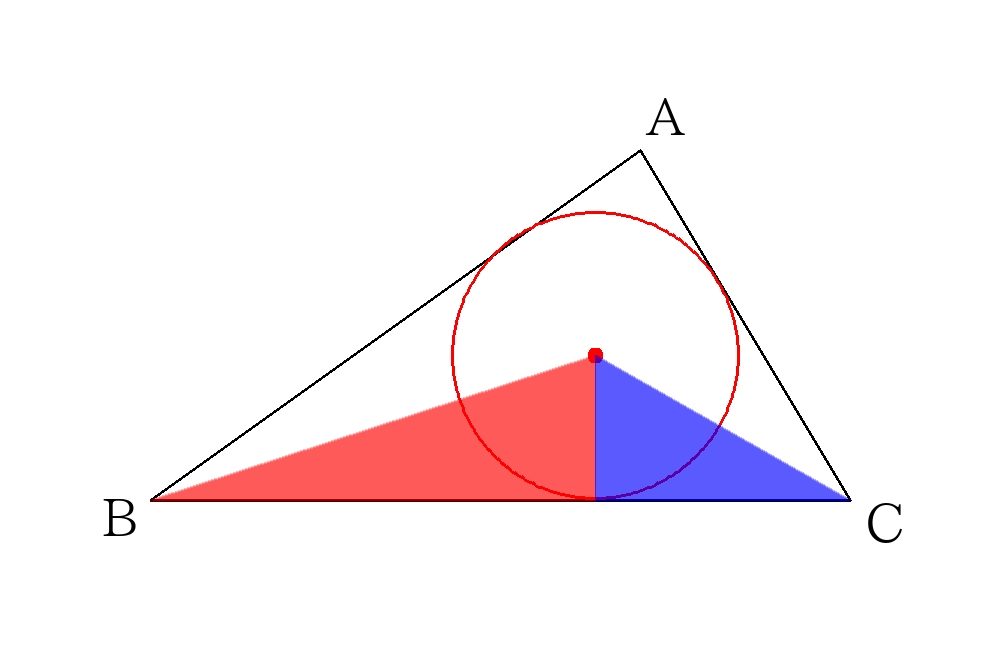
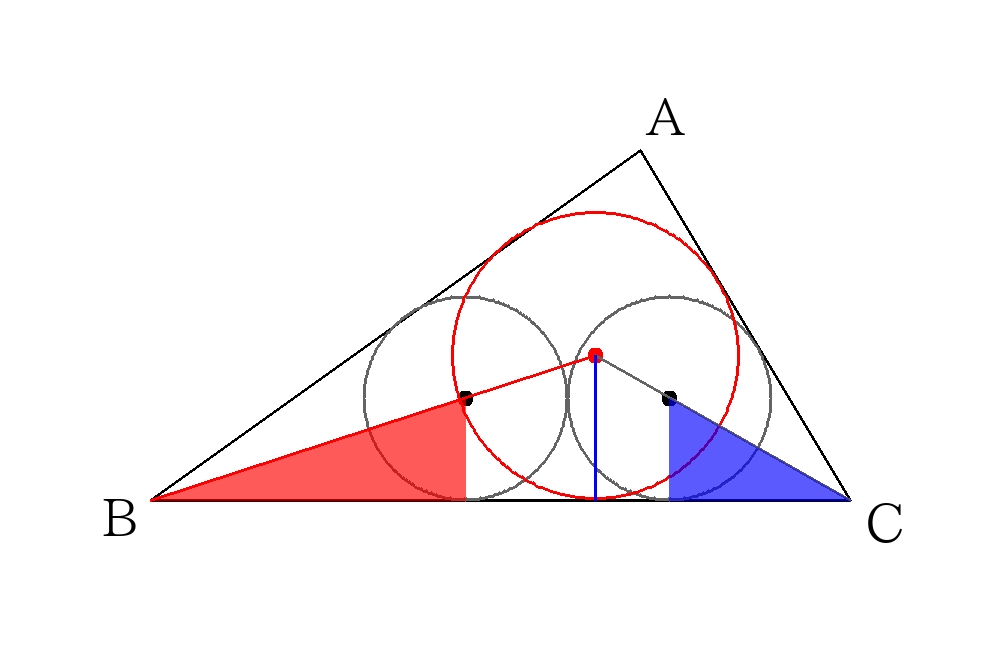
色がついた三角形どうしが相似であることを利用する。
そのために内接円が1つのときの様子を書いて調べてから解く。
解答
- 長方形\(ABCD\)があり、2つの円\(O1\)と\(O2\)が次の図のように内接している。このとき\(O2\)の半径を
求めなさい。 - 直角三角形\(ABC\)に半径が等しい2つの円\(O1\)と\(O2\)が次の図のように内接している。このとき\(O1\)、\(O2\)の半径を求めなさい。
中心と接点をすべて結び、長さの関係を書き入れると次の図のようになる。
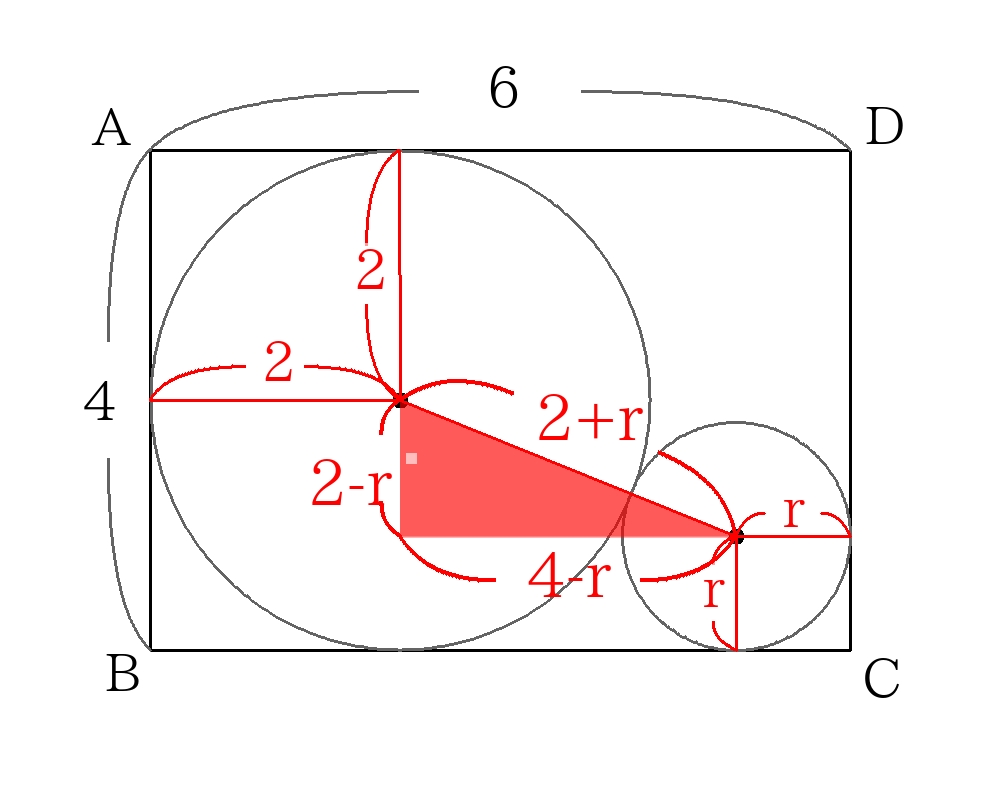
赤い塗りつぶしの直角三角形において三平方の定理より
\((2+r)^2=(2-r)^2+(4-r)^2 \)
\(4+4r+r^2=4-4r+r^2+16-8r+r^2 \)
\(r^2-16r+16=0 \)
\(r=8± 4\sqrt{2} \)
図より\(r< 4\)なので
\(r=8- 4\sqrt{2} \)
内接円が1つのときのようすを書き、長さの関係を書き入れる。
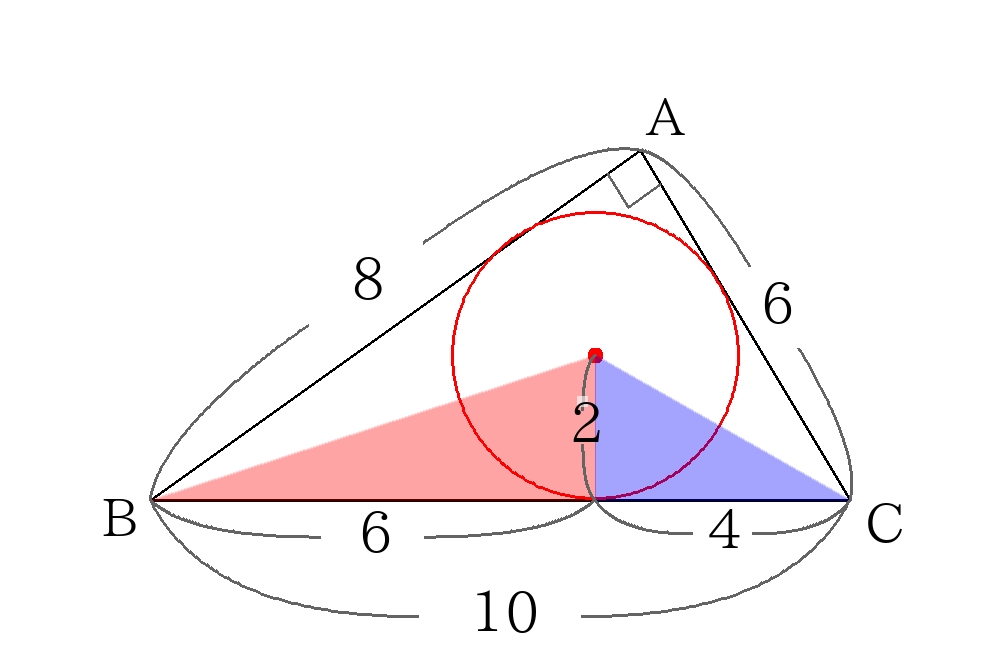
このとき、赤い三角形の縦と横の辺の比は\(3:1\)、青い三角形の縦と横の辺の比は\(2:1\)なので、
次のように長さを書き込む。
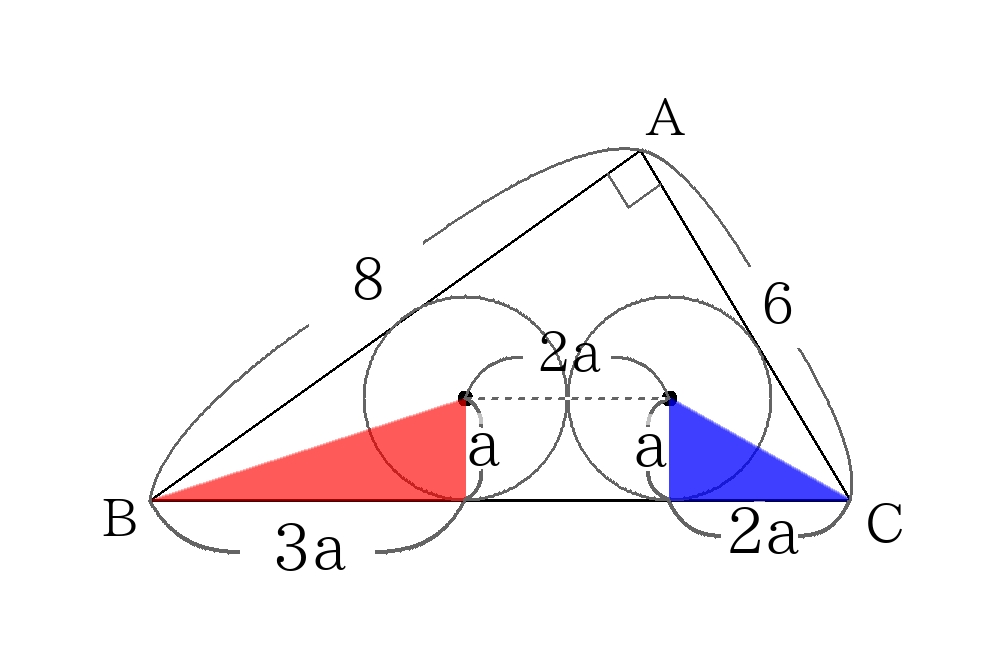
\(BC\)の長さに注目すると、
\(3a+2a+2a=10 \)
\(a= \dfrac{10}{7} \)



コメント