範囲を表す
- \(-4≦x≦-1\),\(2≦y≦5\)のとき、\(2x-3y\)の範囲を不等式で表しなさい。
- \(-3<x≦-1\),\(-2≦y≦4\)のとき、\(-3x+2y\)の範囲を不等式で表しなさい。
- 2つの自然数\(x,y\)があり、小数第二位を四捨五入すると\(x=5.2,y=8.6\)になるという。このとき\(-3x+y\)の範囲を不等式で表しなさい。
- \(-5≦x≦3\),\(-5≦y≦-2\)のとき、\(x^2-y^2\)の範囲を不等式で表しなさい。
- \(x,y\)があり、\(x+y=6\)、\(-3< x < 0\)になるとき、積\(xy\)の範囲を不等式で表しなさい。
- 2つの自然数\(x,y\)があり、\(x+y=13\)、\(-3< x-2y< 0\)になるとき、\(x,y\)をそれぞれ求めなさい。
- 項ごとの範囲を足せ
※引き算をすると範囲が逆になるため、「足す」ことを考える。
例)\(x^2-5x+3y\)の範囲の場合、\((x^2)+(-5x)+(3y)\)と考える。
足し合わせる前に\((x^2)、(-5x)、(3y)\)の範囲をそれぞれ求めておく。 - \(\leqq\)と\(\lt\)を足し合わせると\(<\)になる。
\( \begin{eqnarray}
-1 \color{ #ff0000 }{<} &x& ≦5 \\
+) 2 \color{ #ff0000 }{≦} &x& ≦4 \\
\hline
-1 \color{ #ff0000 }{<} &x& ≦5
\end{eqnarray} \)
※例えば2以上の数と3より大きい(3は入らない)数の和で5になることはない。
- \(x^2\)の範囲は二次関数の変域で考えること。
例) \(-2≦x≦4\)のとき、\(0≦x^2≦16\)
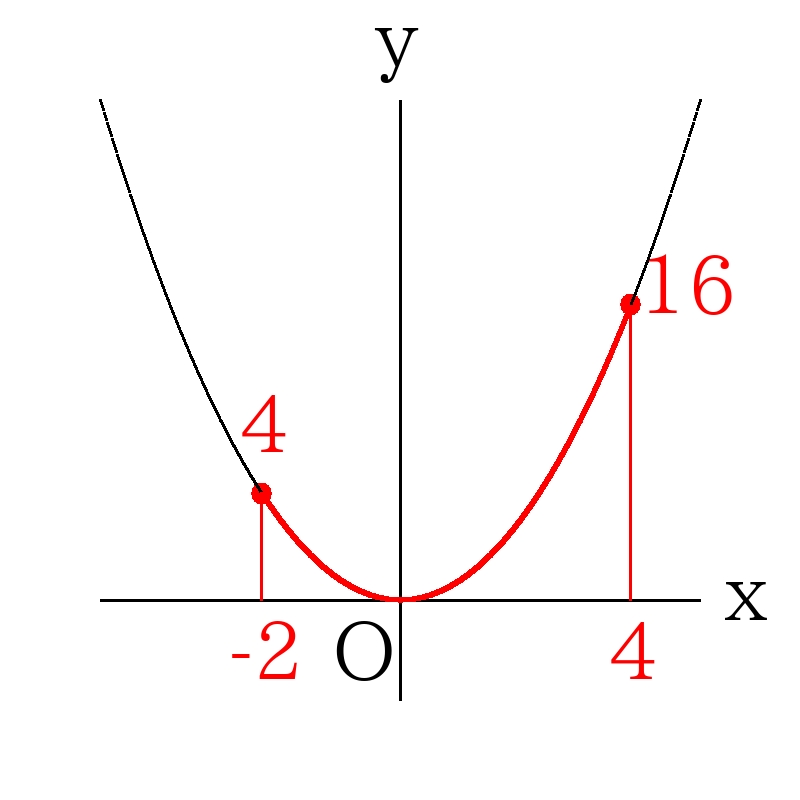
例) \(2≦x≦4\)のとき、\(4≦x^2≦16\)
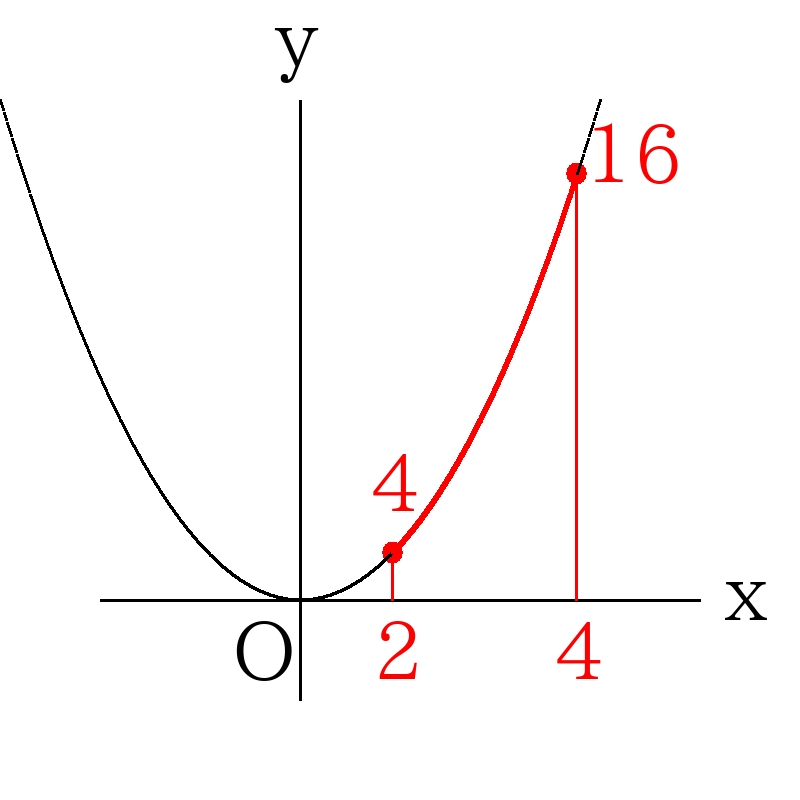
- 四捨五入の範囲の求め方
四捨五入した部分の下に5を書き入れ、それを引いた数と足した数で挟み込む。
例)十の位を四捨五入して700になる数\(x\)
百の位 十の位 一の位 7 0 0 5 0 引くと650、足すと750なので、一の位を四捨五入して70になる数\(x\)の範囲は\(650≦x<750\)
※四捨五入の範囲は「~以上~未満」で表す。
- \(-4≦x≦-1\)、\(2≦y≦5\)のとき、\(2x-3y\)の範囲を不等式で表しなさい。
- \(-3<x≦-1\),\(-2≦y≦4\)のとき、\(-3x+2y\)の範囲を不等式で表しなさい。
- 2つの自然数\(x,y\)があり、小数第二位を四捨五入すると\(x=5.2,y=8.6\)になるという。このとき\(-3x+y\)の範囲を不等式で表しなさい。
- \(-5≦x≦3\),\(-5≦y≦-2\)のとき、\(x^2-y^2\)の範囲を不等式で表しなさい。
- \(x,y\)があり、\(x+2y=0\)、\(-3< x < 2\)になるとき、積\(xy\)の範囲を不等式で表しなさい。
- 2つの自然数\(x,y\)があり、\(x+y=13\)、\(-3< x-2y< 0\)になるとき、\(x,y\)をそれぞれ求めなさい。
それぞれの項を不等式で表してから足し合わせる。
※マイナスをかけると不等式の大小関係が逆になるので注意
\( \begin{eqnarray}
-8 ≦ &2x& ≦-2 \\
+) -15 ≦ &-3y& ≦-6 \\
\hline
-23 ≦ &2x-3y& ≦-8
\end{eqnarray} \)
\(-23≦2x-3y≦-8 \)
それぞれの項を不等式で表してから足し合わせる。
\( \begin{eqnarray}
3 ≦ &-3x& \color{ #ff0000 }{<} 9 \\
+) -4 ≦&2y& \color{ #ff0000 }{≦} 8 \\
\hline
-1 ≦ &-3x+2y& \color{ #ff0000 }{<}17
\end{eqnarray} \)
\(-1≦-3x+2y<17 \)
\(x,y\)の範囲をそれぞれ求めると
\( \begin{eqnarray}
5.15 ≦ &x& < 5.25 \\
8.55 ≦&2y& < 8.65 \\
\end{eqnarray} \)
それぞれの項を不等式で表してから足し合わせる。
\( \begin{eqnarray}
-15.75 < &-3x& ≦ -15.45 \\
+) 8.55 ≦&y& < 8.65 \\
\hline
-7.2 < &-3x+y& < -6.8
\end{eqnarray} \)
\(-7.2<-3x+y<-6.8 \)
\(x,y\)の範囲をそれぞれ求めると
\( \begin{eqnarray}
0 ≦ &x^2& ≦ 25 \\
-25 ≦&-y^2& ≦ -4 \\
\end{eqnarray} \)
それぞれの項を不等式で表してから足し合わせる。
\( \begin{eqnarray}
0 ≦ &x^2& ≦ 25 \\
+) -25 ≦&-y^2& ≦ -4 \\
\hline
-25 < &x^2-y^2& < 21
\end{eqnarray} \)
\(-25< x^2-y^2< 21 \)
\(y\)について解くと\(y=-\dfrac{1}{2}x\)
ここで\(xy=-\dfrac{1}{2}x^2\)
\(0≦x^2<9 \)
\(- \dfrac{9}{2}<- \dfrac{1}{2}x^2≦0 \)
よって
\(- \dfrac{9}{2}< xy≦0 \)
\(y\)について解くと\(y=13-x\)、\(x-2y\)に代入すると\(x-2(13-x)=3x-26\)
\(-3<3x-26<0 \)
すべての辺に26を足すと
\(23<3x<26 \)
すべての辺を3で割ると
\(7 \dfrac{2}{3}< x< 8 \dfrac{2}{3} \)
よって
\(x=8,y=5 \)



コメント