放物線と相似
放物線\(m:y=x^2\)と放物線\(m:y=\dfrac{1}{2}x^2\)があり、2つの放物線と直線\(y=ax\)の交点を\(A\)、\(B\)、2つの放物線と直線\(y=bx\)の交点を\(C\)、\(D\)、原点を\(O\)とする。
(\(a>0,b<0\))
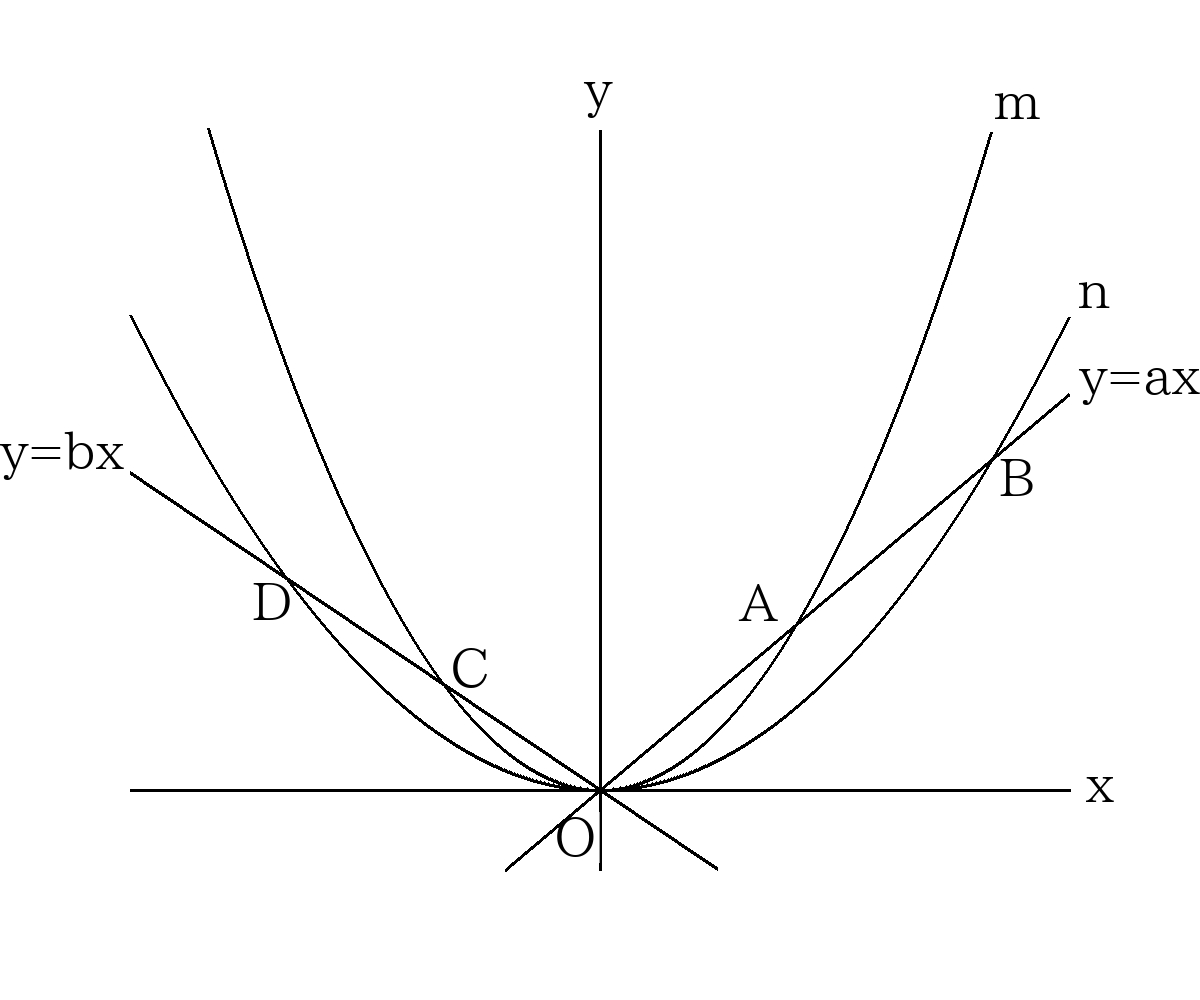
- \(\triangle OAC\)と\(\triangle OBD\)の面積の比を求めなさい。
- \(AB=\sqrt{2}\)のとき\(a^2\)の値を求めなさい。
- すべての放物線は相似である。(縮尺を変えれば重なるため。)
- \(y=ax^2\)、\(y=bx^2\)のような中学範囲で学習する放物線は頂点が原点にくるため、相似の中心は原点である。
よって、次の関係が成り立つ。
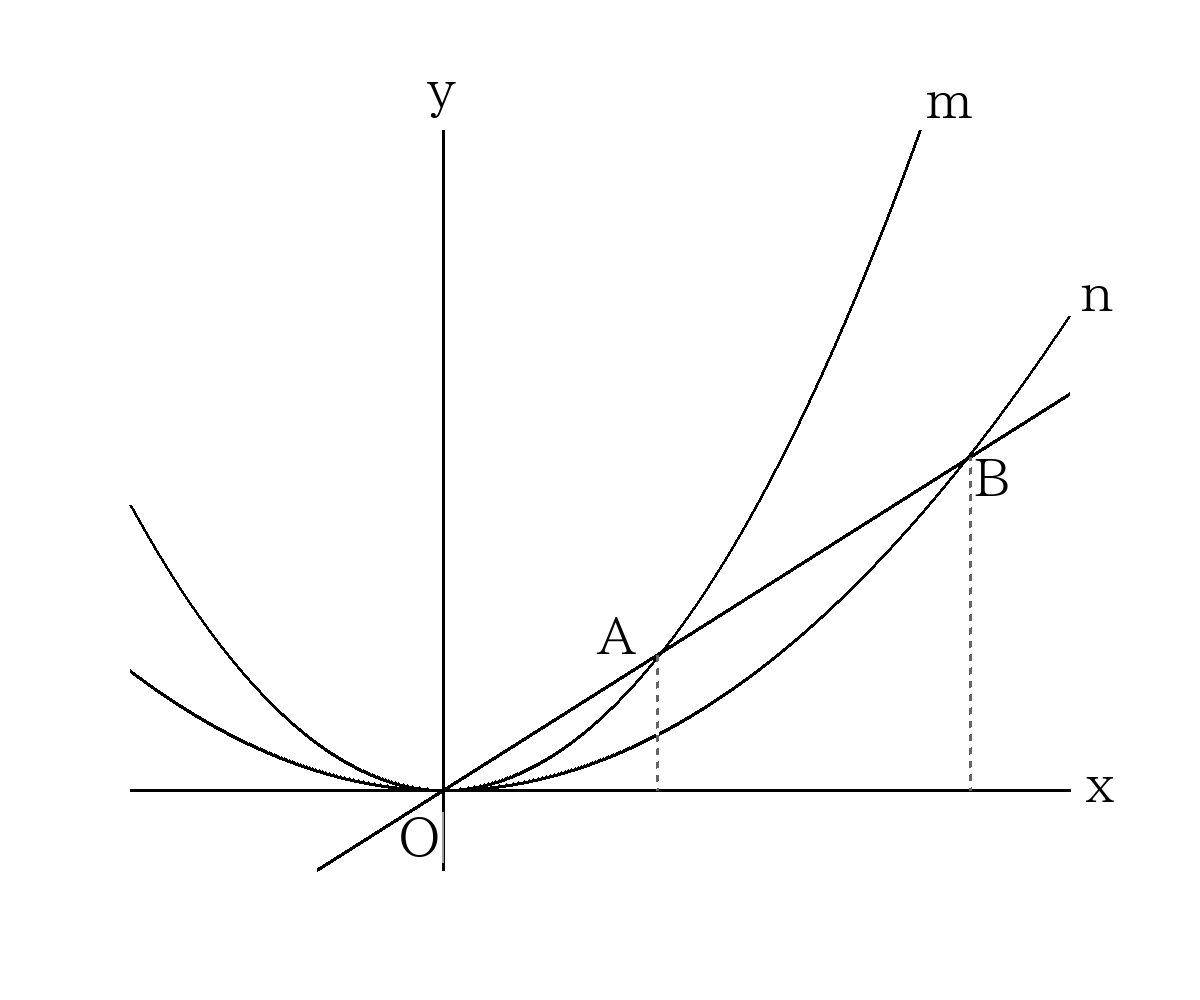
2つの放物線\(m:y=ax^2\)、\(n:y=bx^2\)があり原点を通る直線との交点を\(A,B\)とするとき、
\(OA:OB=b:a\)(放物線の係数の絶対値の逆比の関係)になる。
【証明】
2つの放物線\(m:y=ax^2\)、\(n:y=bx^2\)と直線\(y=cx\)との交点を\(A,B\)とする。
\(A\)の\(x\)座標を求める。\(y=ax^2\)と\(y=cx\)を連立させれば良い。\(x=\dfrac{c}{a}\)
同様に\(B\)の\(x\)座標は\(x=\dfrac{c}{b}\)
よって\(OA:OB\)の\(x\)方向の長さの比は\(OA_{x}:OB_{x}=\dfrac{c}{a}:\dfrac{c}{b}=b:c\)
\(A,B\)から\(x\)軸に垂線をそれぞれ下すと、三角形の相似より\(OA:OB=OA_{x}:OB_{x}=b:c\)
- 放物線\(m:y=x^2\)と放物線\(m:y=\dfrac{1}{2}x^2\)があり、2つの放物線と直線\(y=ax\)の交点を\(A\)、\(B\)、2つの放物線と直線\(y=bx\)の交点を\(C\)、\(D\)、原点を\(O\)とする。
- \(\triangle OAC\)と\(\triangle OBD\)の面積の比を求めなさい。
- \(AB=\sqrt{2}\)のとき\(a^2\)の値を求めなさい。

放物線の相似より、\(OA:OB=OC:OD=\dfrac{1}{2}:1=1:2\)
よって、\(\triangle OAC\)と\(\triangle OBD\)は\(1:2\)の相似形でありその面積比は\(1^2 : 2^2=1:4\)
\( \triangle OAC: \triangle OBD=1:4 \)
\(y=x^2\)と\(y=ax\)の交点より、\(A(a,a^2)\)
\(y=\dfrac{1}{2}x^2\)と\(y=ax\)の交点より、\(B(2a,4a^2)\)
三平方の定理より
\( AB^2=(2a-a)^2+(4a^2-a^2)^2=9a^4+a^2 \)
\(AB=\sqrt{2}\)より
\(9a^4+a^2=2\)
\(9a^4+a^2-2=0\)
ここで\(a^2=t\)とおくと、
\(9t^2+t^2-2=0\)
\(t=a^2=\dfrac{-1 ± \sqrt{73}}{18}\)
\(a>^2\)より\(a^2=\dfrac{-1 + \sqrt{73}}{18}\)
\(a^2= \dfrac{-1+ \sqrt{73}}{18} \)



コメント