円の重なりと接弦定理
次の図のように大小2つの円が点\(D\)で接しており、\(FG\)は点\(D\)における2つの円の共通接線、\(AB\)は点\(C\)における小さな円の接線である。
\(\angle DAB=45°\)、\(\angle ADF=75°\)、\(DB=6cm\)のとき次の問に答えなさい。
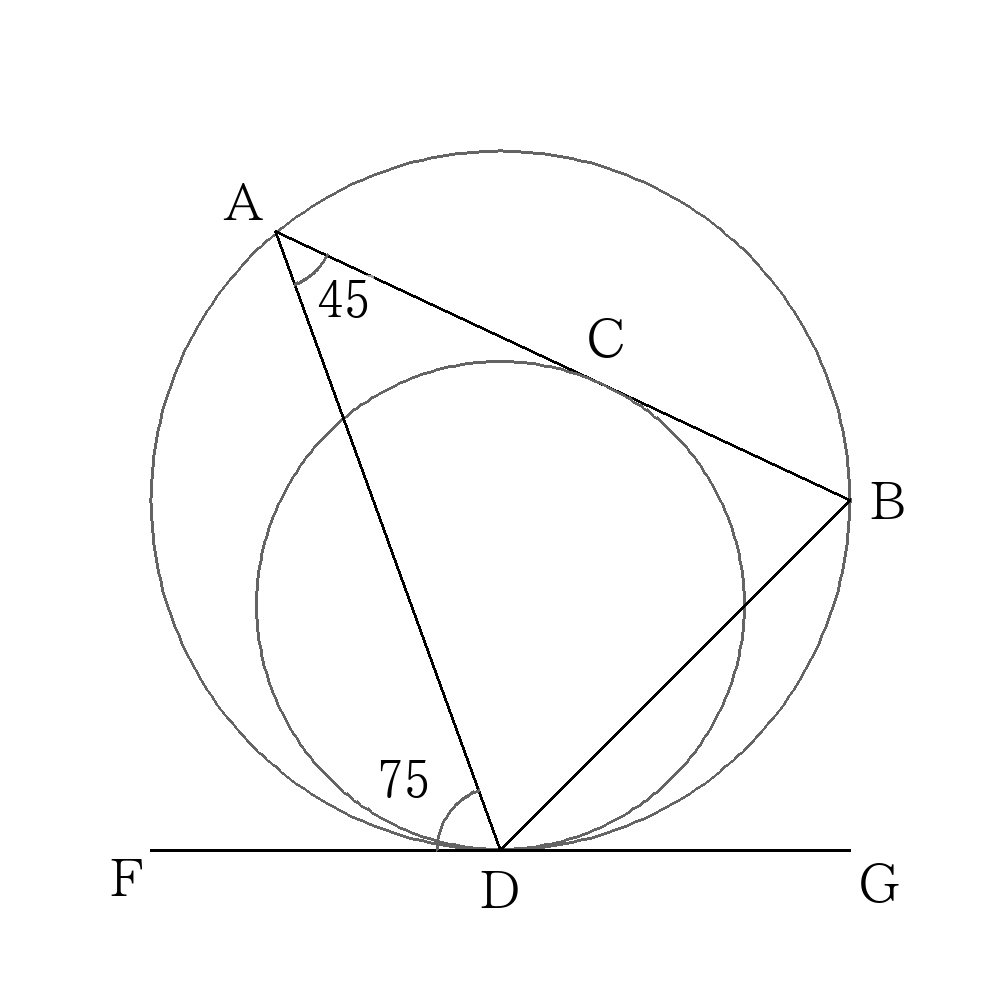
- \(BC\)の長さを求めなさい。
- 大きい円の直径を求めなさい。
- 角の二等分線を使う。(\(\angle EDC=\angle CDB\))
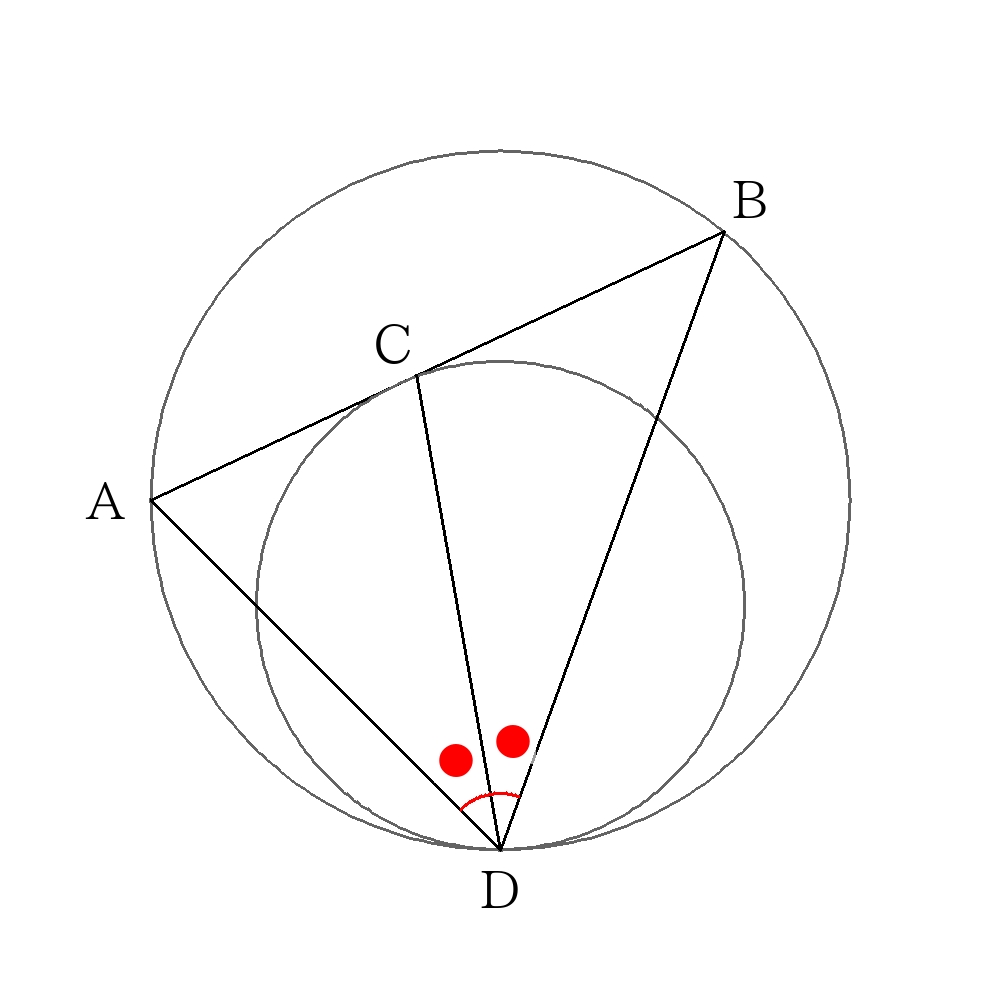
※特にこの形は意識をして覚えておくこと。毎回導くのは時間がもったいない。 - 相似形を使う。(\(\triangle DEC\)∽\(\triangle DCB\))
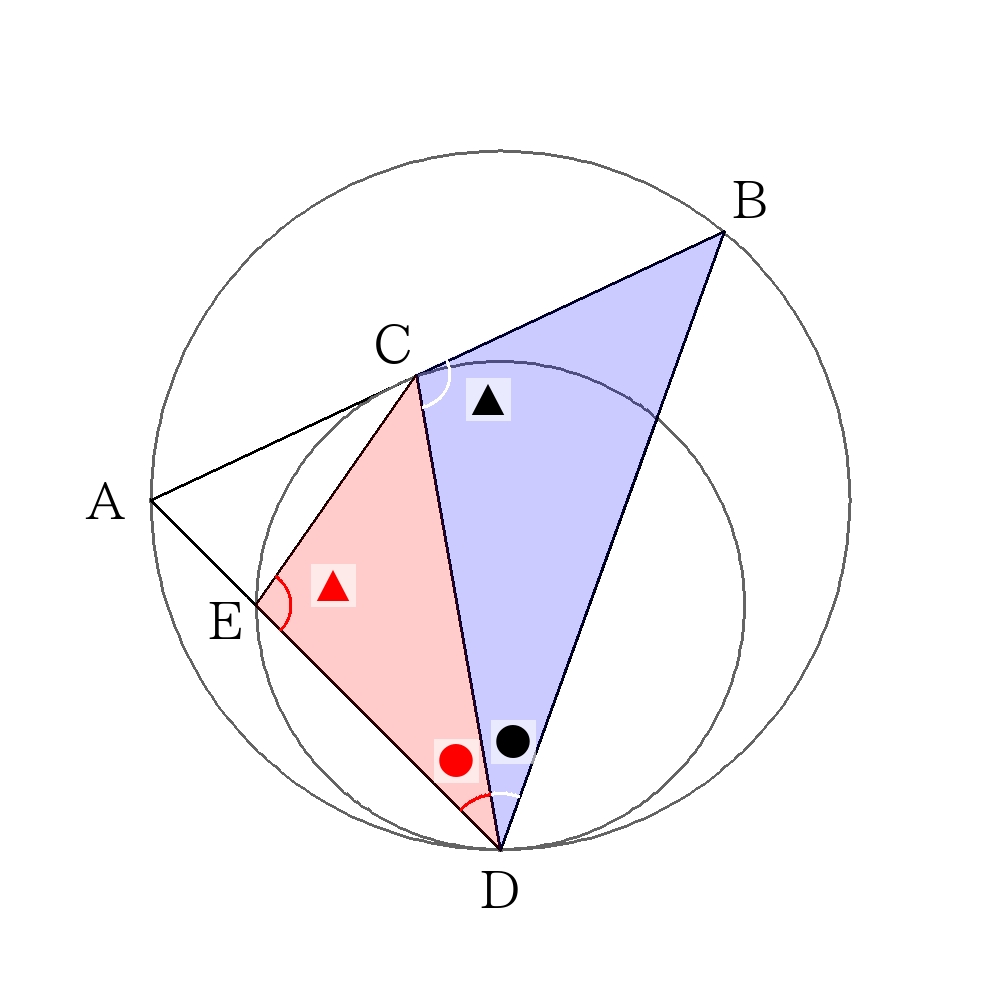
1.角の二等分線になることの証明
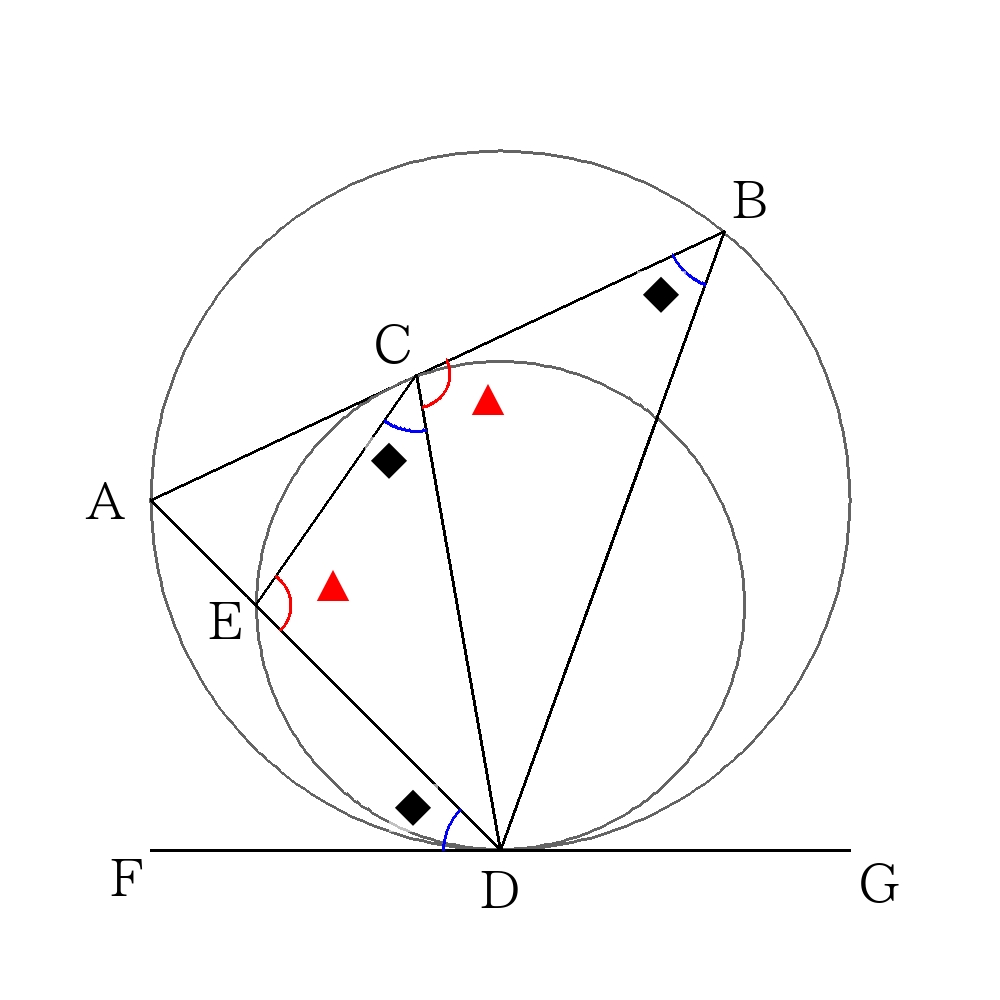
接点\(D\)を通る接線\(FG\)を引く。
接線\(FG\)と小さい円に注目し、接弦定理を利用すると、
\( \angle ADF= \angle ECD \dots ①\)
接線\(FG\)と大きい円に注目し、接弦定理を利用すると、
\( \angle ADF= \angle ABD(CBD) \dots ②\)
①、②より
\( \angle ECD= \angle CBD \dots ③\)
接線\(AB\)と小さい円に注目し、接弦定理を利用すると、
\( \angle DEC= \angle DCB \dots ④\)
③、④より2組の角がそれぞれ等しいので、\( \triangle DEC \)∽\( \triangle DCB \)
相似な図形の対応する角は等しいので
\( \angle EDC= \angle CDB \)
2.相似になることの証明 →1.の証明の途中で証明済み
- 次の図のように大小2つの円が点\(D\)で接しており、\(FG\)は点\(D\)における2つの円の共通接線、\(AB\)は点\(C\)における小さな円の接線である。
- \(BC\)の長さを求めなさい。
- 大きい円の直径を求めなさい。
\(\angle DAB=45°\)、\(\angle ADF=75°\)、\(DB=6cm\)のとき次の問に答えなさい。

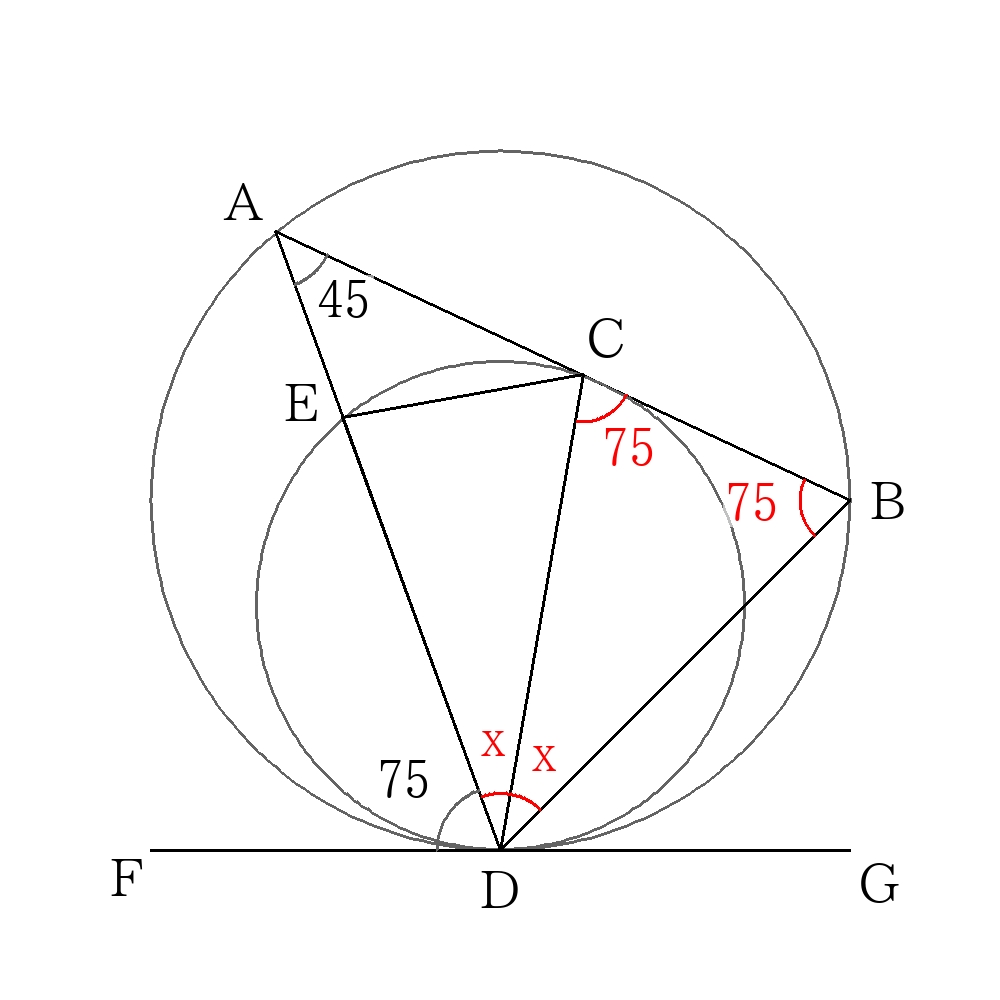
\(AD\)と小さな円との交点を\(E\)とする。また、\(CD\)を結ぶと\(CD\)は\(\angle ADB\)の二等分線である。
また接線\(FG\)と大きな円の接弦定理より、
\( \angle ABD=ADF=75° \)
ここで、\( \angle ADC= \angle BDC=x \)とおくと、\( \triangle ADB \)の内角の和より
\(2x+45+75=180 \)
\(x=30° \)
\( \triangle CBD \)の内角の和より
\( \angle BCD=75 \)
\(\triangle DCB\)は頂角30°、底角75°、\(DB=6cm\)の二等辺三角形として長さを計算する
(※詳しくはこちら→特別角の三角形)
\(BC=3 \sqrt{6}-3 \sqrt{2} \)
大きい円の中心\(O\)とDを通る直線を引き、円との交点を\(H\)とし、\(BH\)を結ぶ。
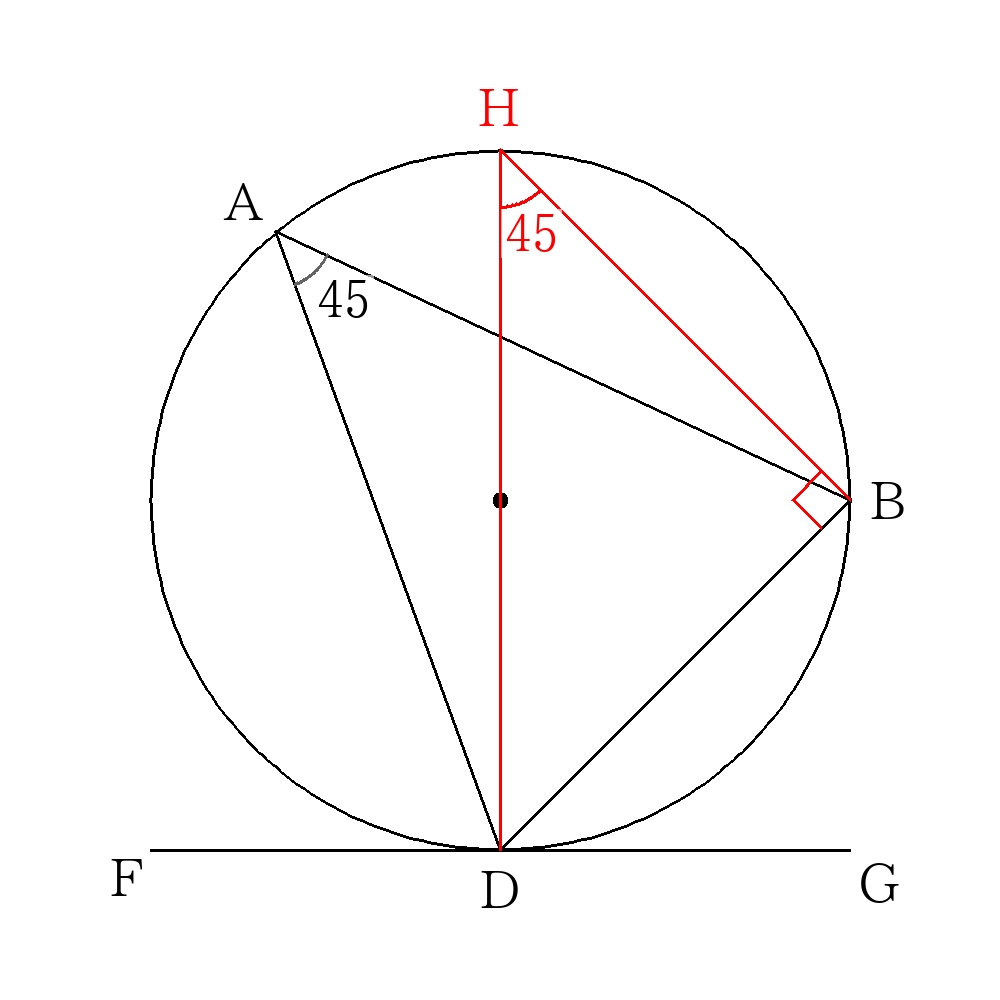
円周角の定理より\(\angle DHB=45°\)、\(\angle HBD=90°\)であり、\(\triangle HBD\)は直角二等辺三角形である。
ここで大きい円の半径を\(r\)とすると、\(\triangle HBD\)において三平方の定理より
\(2r= \sqrt{2} \times DB=6 \sqrt{2} \)
\(r=3 \sqrt{2} \)



コメント