いろいろな立体
それぞれの図形において、内接球と外接球の半径を求めなさい。
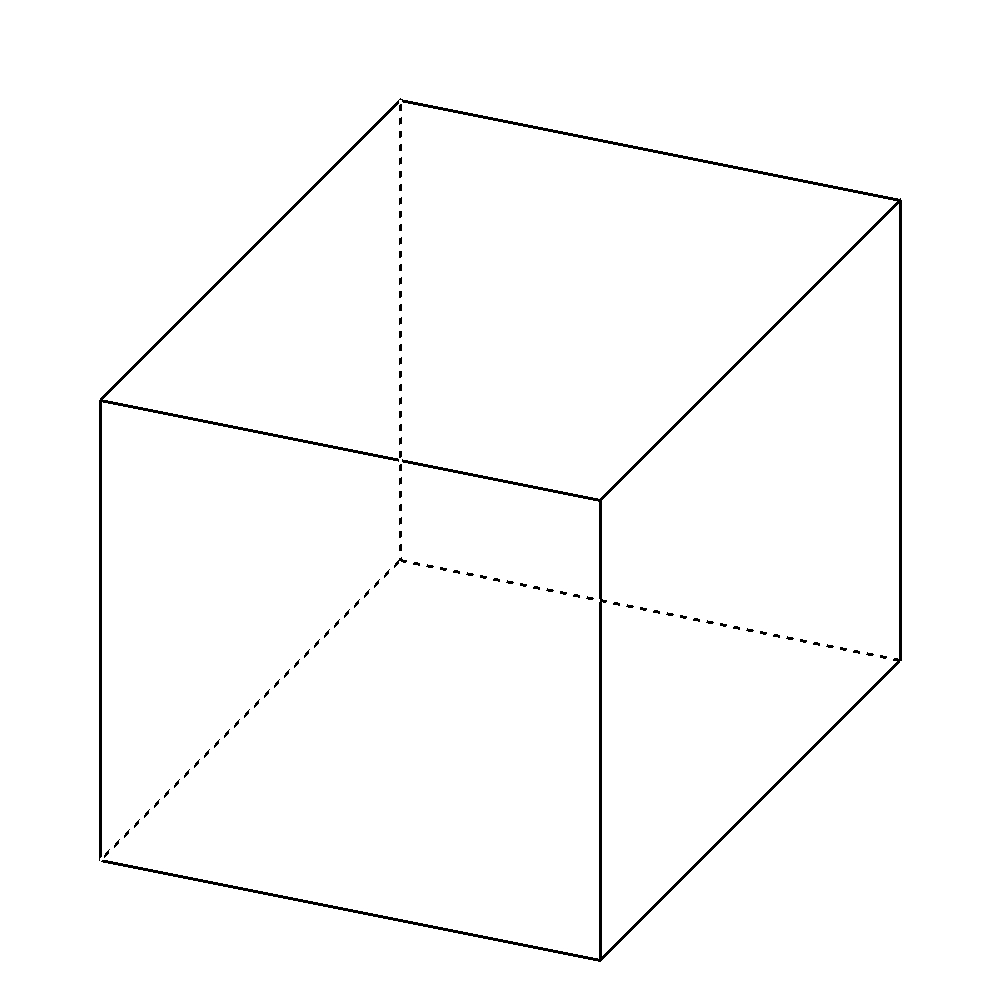
- 1辺の長さが\(a\)の立方体
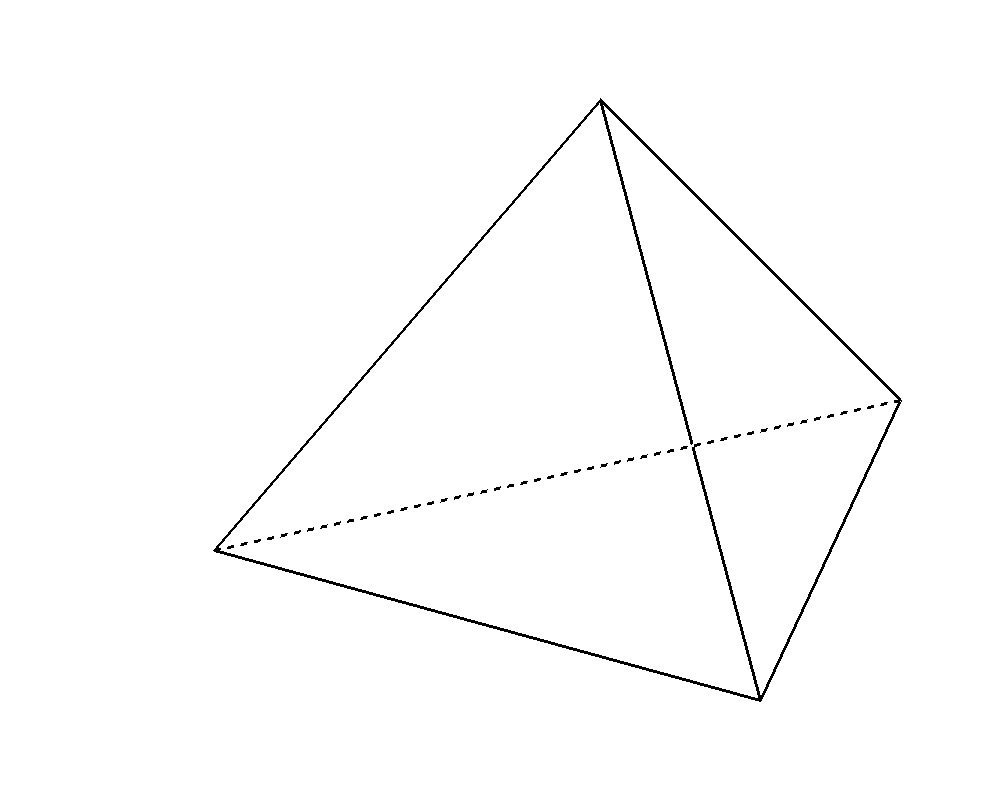
- 1辺の長さが\(a\)の正四面体
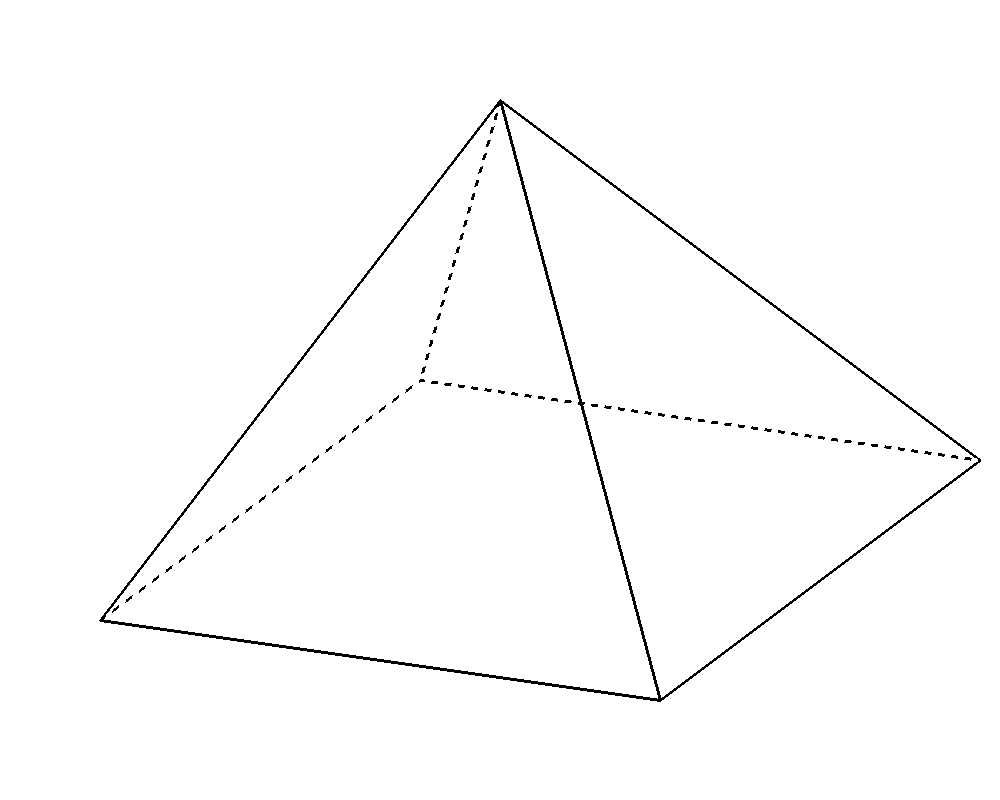
- 1辺の長さがすべて\(a\)の正四角錐
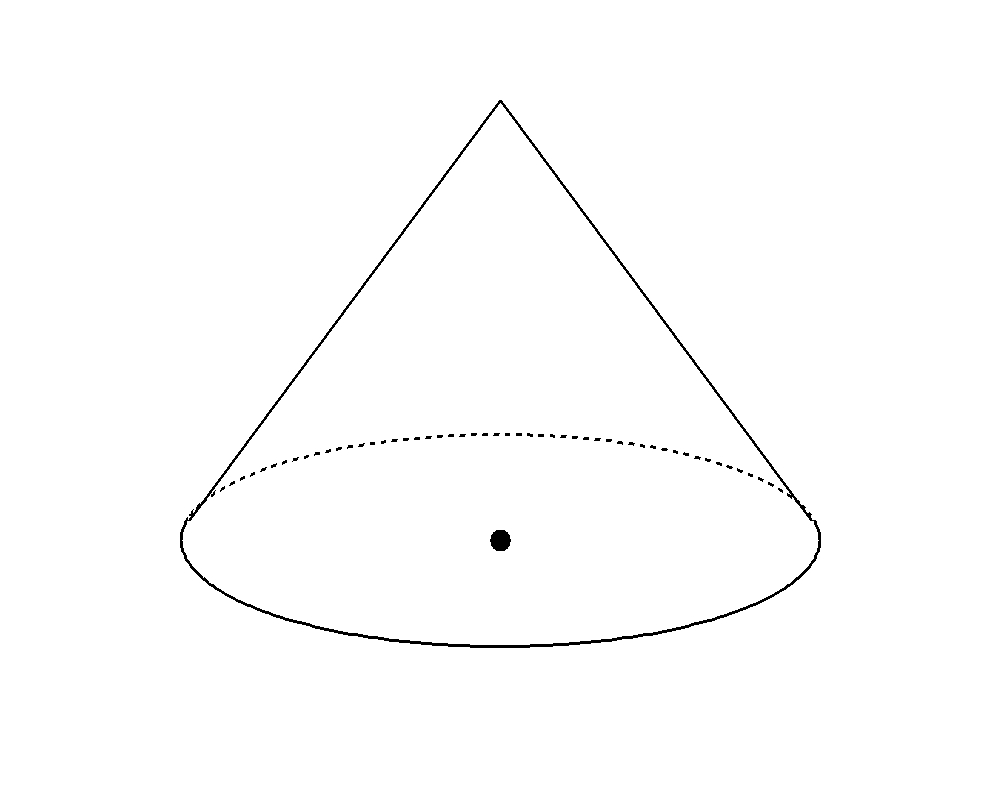
- 半径が\(6\)、母線の長さが\(10\)の円錐
- 球の中心と接点を通る平面で切り抜け!
-
- 1辺の長さが\(a\)の立方体
■内接球の半径を求める。
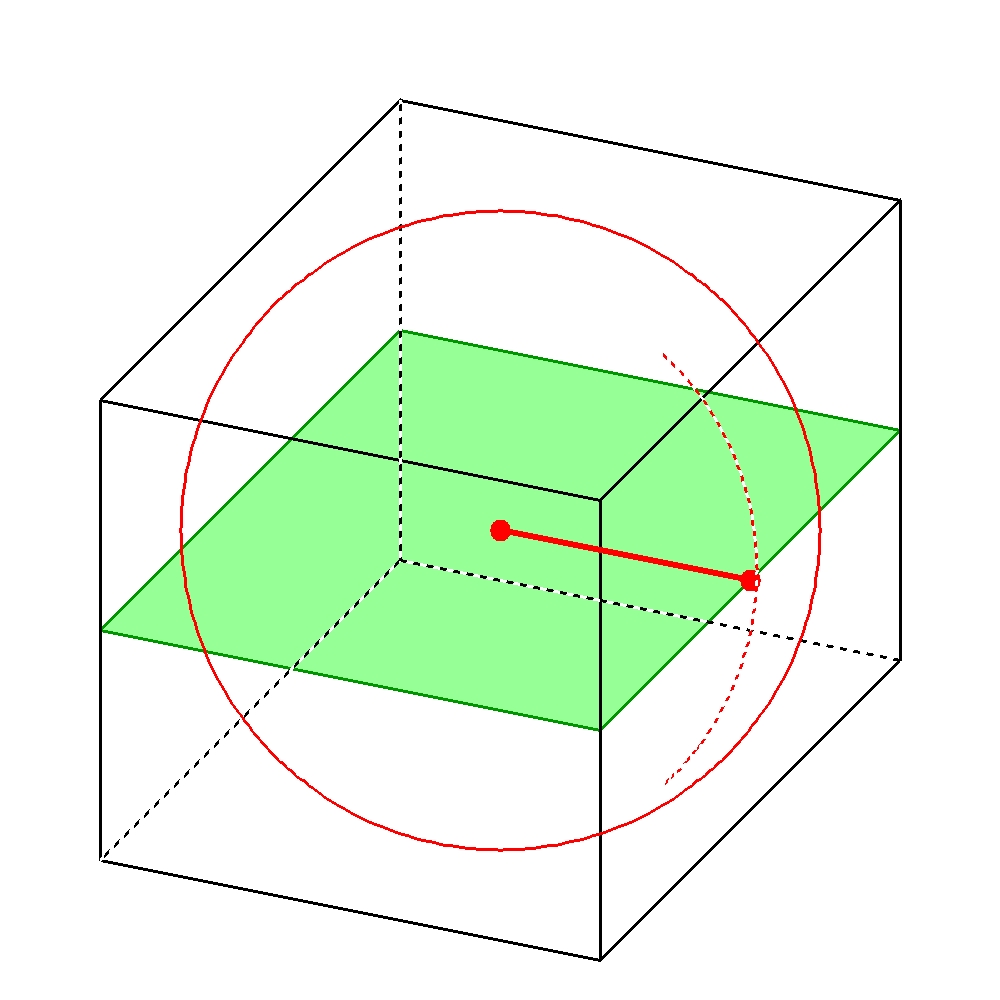
図より内接球の半径は立方体の1辺の長さの半分なので、
\( \dfrac{1}{2}a \)
■外接球の半径を求める。
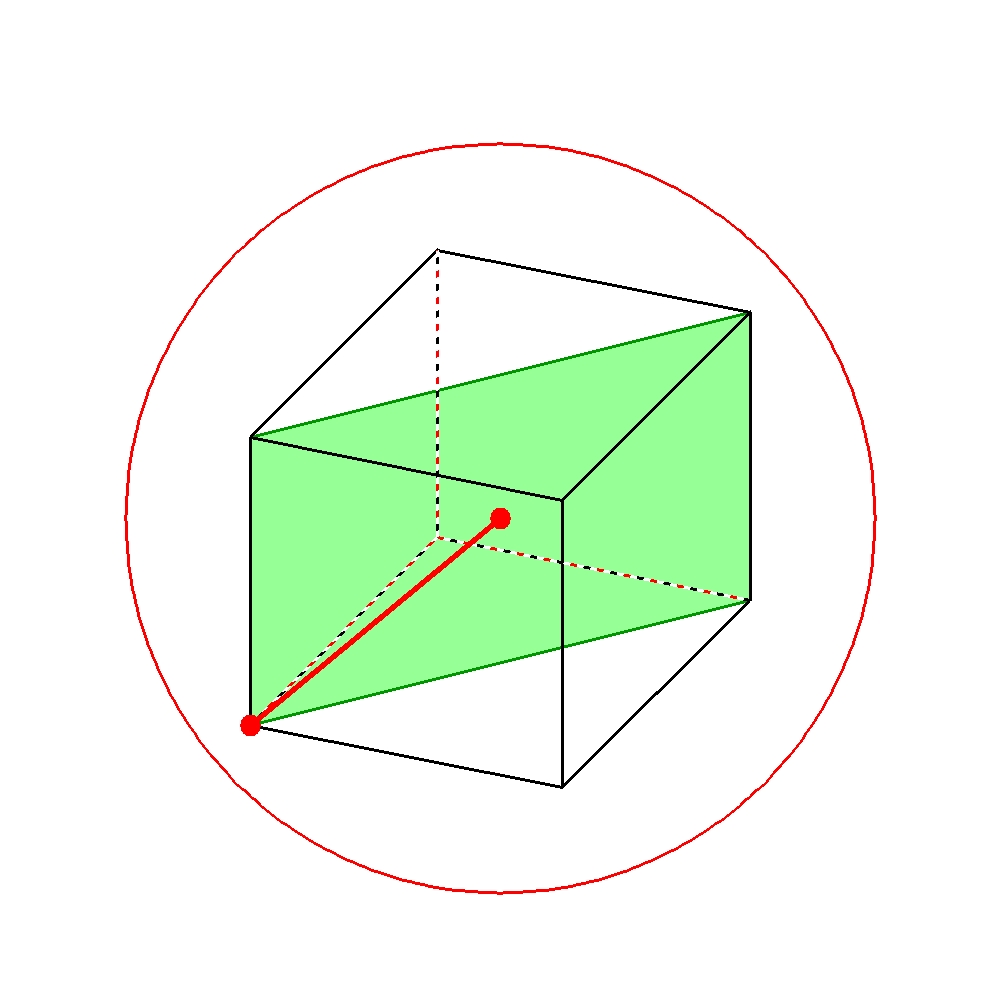
図より外接球の半径は立方体の対角線の長さの半分なので、
\( \dfrac{ \sqrt{3}}{2}a \)
-
- 1辺の長さが\(a\)の正四面体
正四面体については正四面体_基本知識を参考にしてください。
■内接球の半径を求める。
\( \dfrac{ \sqrt{6}}{12}a \)
■外接球の半径を求める。
\( \dfrac{ \sqrt{6}}{4}a \)
-
- 1辺の長さがすべて\(a\)の正四角錐
■内接球の半径を求める。
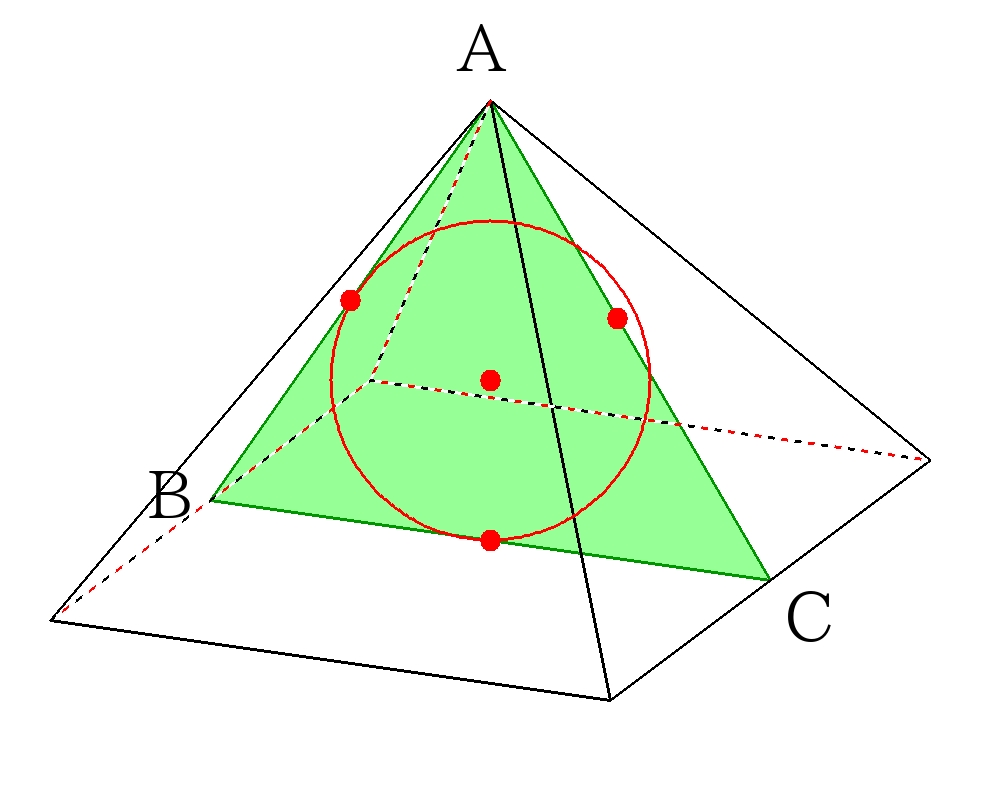
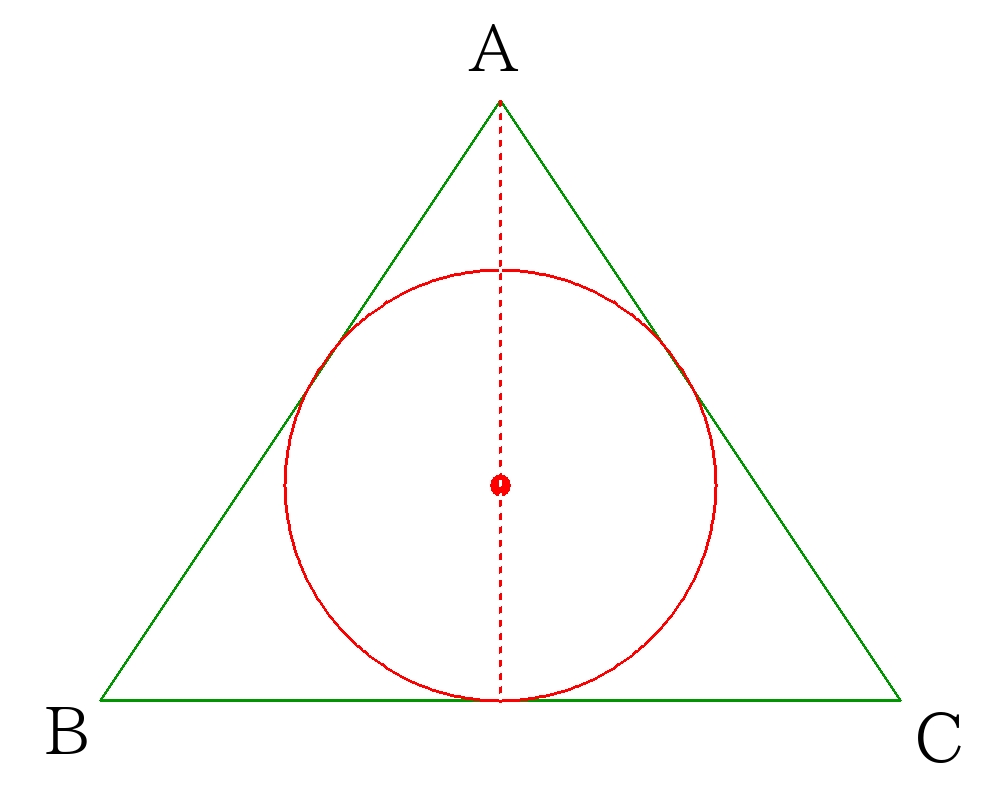
正四角錐を図示した三角形\(ABC\)で切り抜く。球は\(\triangle ABC \)の三辺に接しているので、三角形の内接円の半径を面積から求めれば良い。
正四角錐の側面の正三角形より
\(AB=AC= \dfrac{ \sqrt{3}}{2}a \)
また\(BC=a\)であり、\(\triangle ABC\)の高さを三平方で求めると、
\( \dfrac{ \sqrt{2}}{2}a \)
よって\(\triangle ABC\)の面積は
\(a \times \dfrac{ \sqrt{2}}{2}a \times \dfrac{1}{2}= \dfrac{ \sqrt{2}}{4}a^2 \)
ここで内接円(内接球)の半径を\(r\)とすると、面積の関係より
\( \dfrac{ \sqrt{2}}{4}a^2= \dfrac{1}{2} r \left( \dfrac{ \sqrt{3}}{2}a+ \dfrac{ \sqrt{3}}{2}a+a \right) \)
\(r= \dfrac{ \sqrt{2}}{2( \sqrt{3}+1)}a \)
分母を有理化すると
\(r= \dfrac{ \sqrt{6}- \sqrt{2}}{4}a \)
\(r= \dfrac{ \sqrt{6}- \sqrt{2}}{4}a \)
■外接球の半径を求める。
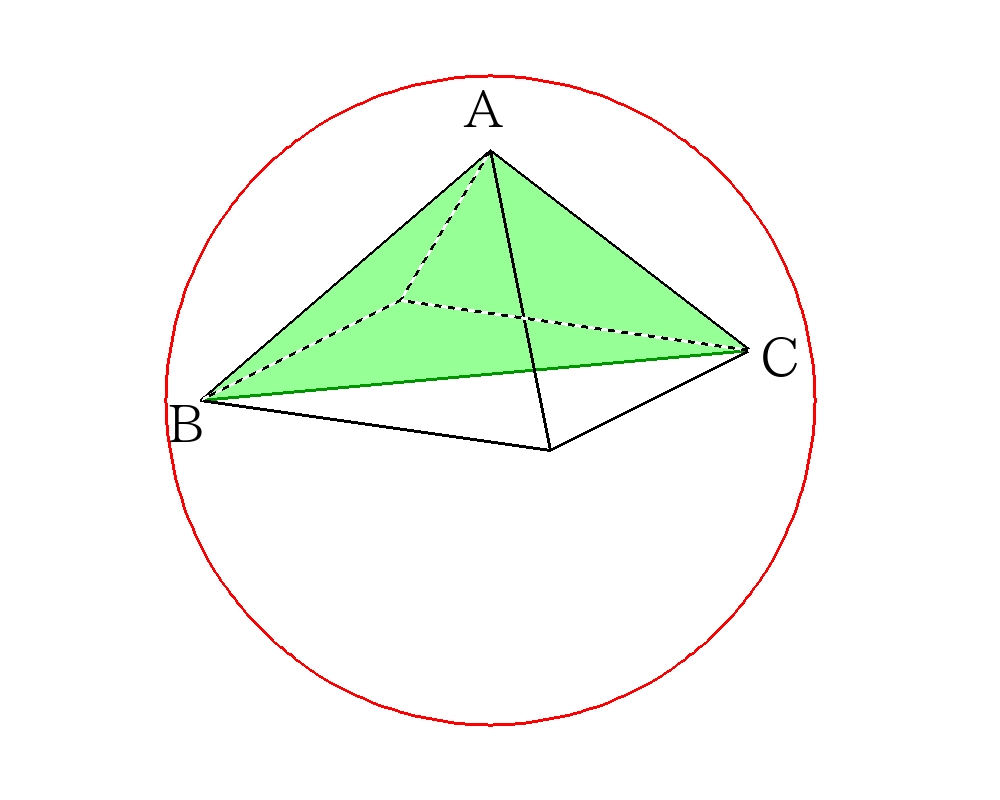
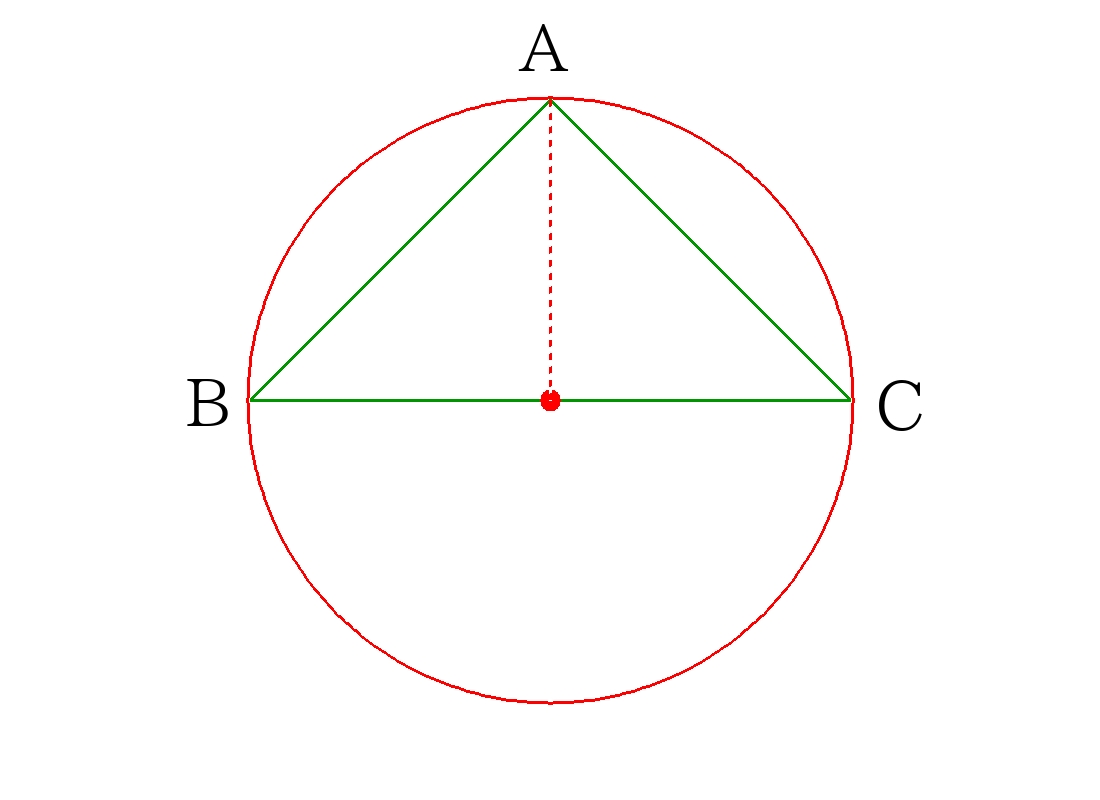
正四角錐を図示した三角形\(ABC\)で切り抜く。球は\(\triangle ABC \)の各頂点に接しているので、三角形の外接円の半径を求めれば良い。
ここで\(AB=AC=a\)、\(BC=\sqrt{2}a\)なので、\(\triangle ABC\)は\(\angle BAC=90\)の直角二等辺三角形である。
よって、外接円(外接球)の中心は\(BC\)の中点と一致する。
\( \dfrac{ \sqrt{2}}{2}a \)
-
- 半径が\(6\)、母線の長さが\(10\)の円錐
■内接球の半径を求める。
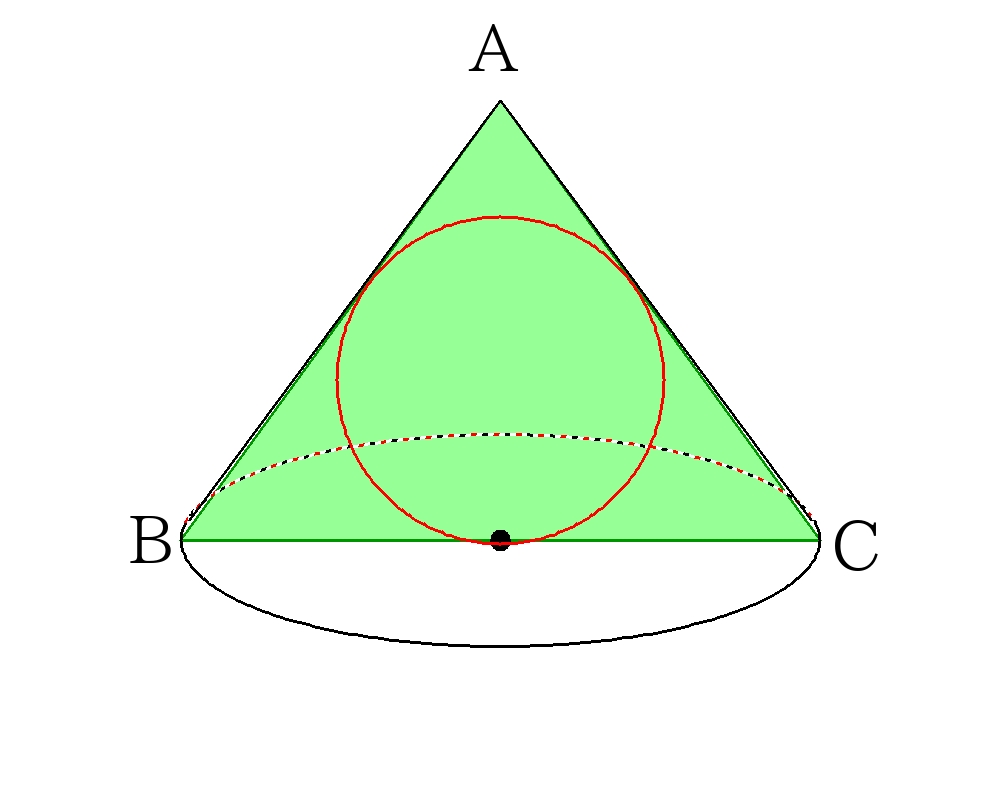
円錐を図示した三角形\(ABC\)で切り抜く。球は\(\triangle ABC \)の三辺に接しているので、三角形の内接円の半径を面積から求めれば良い。
三平方の定理より\(\triangle ABC\)の高さは
\( \sqrt{10^2-6^2}=8 \)
\(\triangle ABC\)の面積は
\(12 \times 8 \times \dfrac{1}{2}=48 \)
ここで内接円(内接球)の半径を\(r\)とすると、面積の関係より
\(48=(12+10+10)r \)
\(r= \dfrac{8}{7} \)
\(r= \dfrac{8}{7} \)
■外接球の半径を求める。
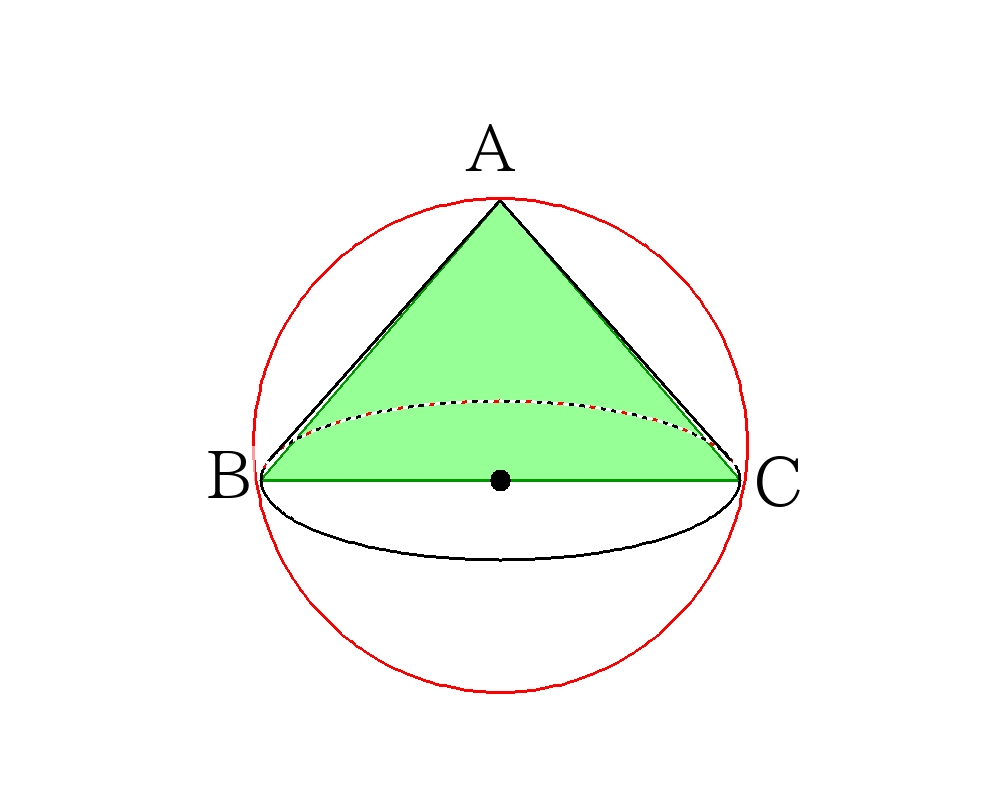
![]()
円錐を図示した三角形\(ABC\)で切り抜く。球は\(\triangle ABC \)の各頂点に接しているので、三角形の外接円の半径を求めれば良い。
\(A\)から\(BC\)に下ろした垂線を\(AH\)とし、外接円の中心を\(O\)とする。
\(\triangle ABH\)において三平方の定理より
\(AH= \sqrt{10^2-6^2}=8 \)
ここで外接円の半径を\(R\)とすると、\(OB=R\)、\(OH=8-R\)
\(\triangle OBH\)において三平方の定理より
\(R^2=(8-R)^2+6^2 \)
\(R= \dfrac{25}{4} \)



コメント
正四角錐の内接球の半径がちがいませんか?
三角形の面積の関係のところの方程式で、1/2されていないと思います。
ご指摘ありがとうございます。その通りでございます。
本日、修正いたしました。
貴重なお時間取らせてしまい、申し訳ありませんでした。
引き続きよろしくお願いいたします。