2次関数
放物線と直線の式
例題
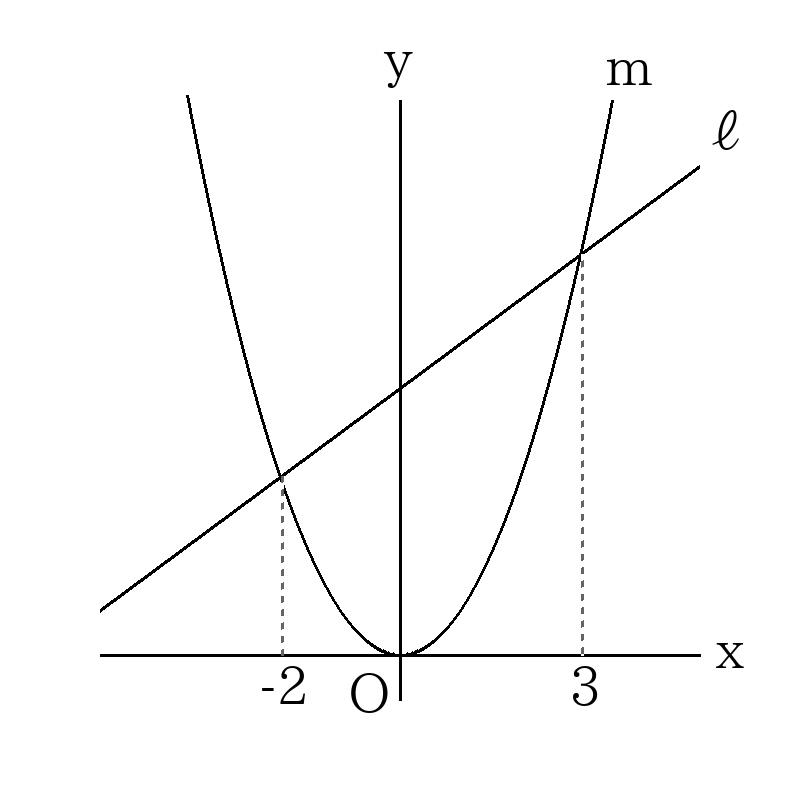
- 放物線\(m:y=2x^2\)と直線\(l\)が次の図のように交わっているとき、直線\(l\)の式を求めなさい。
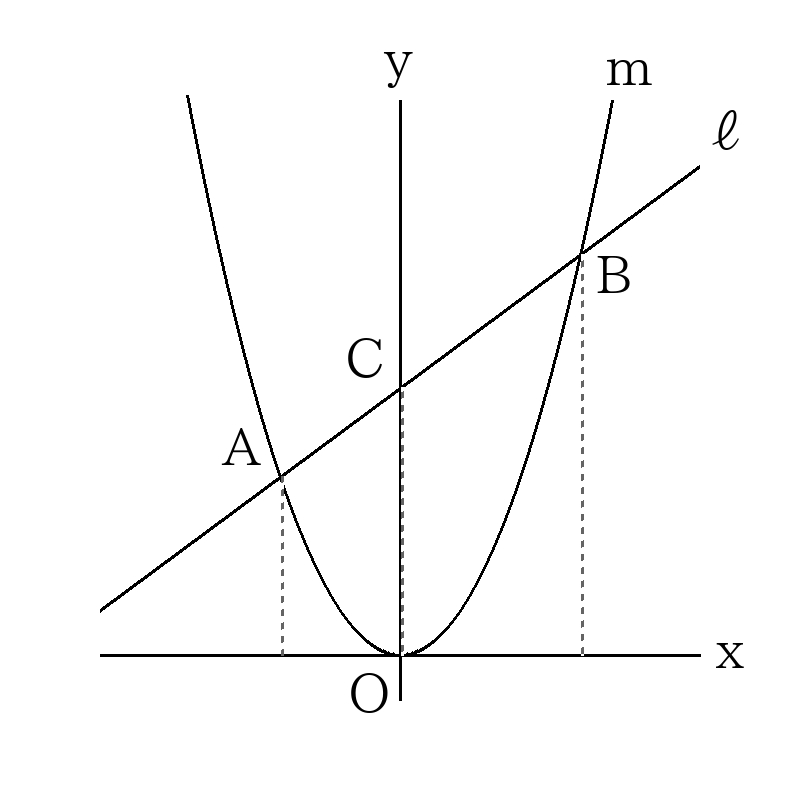
- 次のグラフで放物線\(m\)と直線\(ℓ\)は2点\(A,B\)で交わっていて、点\(C(0,6)\)である。
点\(A,B\)が格子点上にあるとき、直線\(ℓ\)の式として考えられるものを答えなさい。なお直線\(ℓ\)の傾きは正とする。
まずはこう解け!
\(y=ax^2\)と\(y=bx+c\)が2点\(A(p,0),B(q,o)\)で交わっているとき次の関係が成り立つ。
- \(b=a(p+q)\)
- \(c=-apq\)
つまり直線の式は\(y=a(p+q)x-apq\)
※証明は省略。代入して式の変形をすればすぐに証明できる。
解答
- 放物線\(m:y=2x^2\)と直線\(l\)が次の図のように交わっているとき、直線\(l\)の式を求めなさい。

- 次のグラフで放物線\(m:y=\dfrac{1}{2}x^2\)と直線\(ℓ\)は2点\(A,B\)で交わっていて、点\(C(0,6)\)である。
点\(A,B\)が格子点上にあるとき、直線\(ℓ\)の式として考えられるものを答えなさい。なお直線\(ℓ\)の傾きは正とする。

公式通りに解けば良い。
直線\(ℓ\)の式を\(y=bx+c\)とすると、
\(b=2(-2+3)=2\)
\(c=-2 \times (-2) \times 3=12 \)
\(y=2x+12 \)
公式に当てはめる。
\(A,B\)のx座標をそれぞれ\(p,q(p<0,q>0)\)とし、直線\(ℓ\)の式を\(y=bx+6\)とすると、
\(6=- \dfrac{1}{2} \times p \times q \)
\(pq=-12\)を満たす組み合わせを見つければ良い。
\((p,q)=(-12,1),(-6,2),(-4,2),(-3,4),(-2,6),(-1,12)\)
このうち傾きが正になるためには\(\dfrac{1}{2}(p+q)>0→q>-p\)を満たす必要があるので、
\((p,q)=(-3,4),(-2,6),(-1,12)\)
あとはそれぞれの式を求めれば良い。
\(y= \dfrac{1}{2}x+6,y=2x+6,y= \dfrac{11}{2}x+6 \)



コメント