接する球
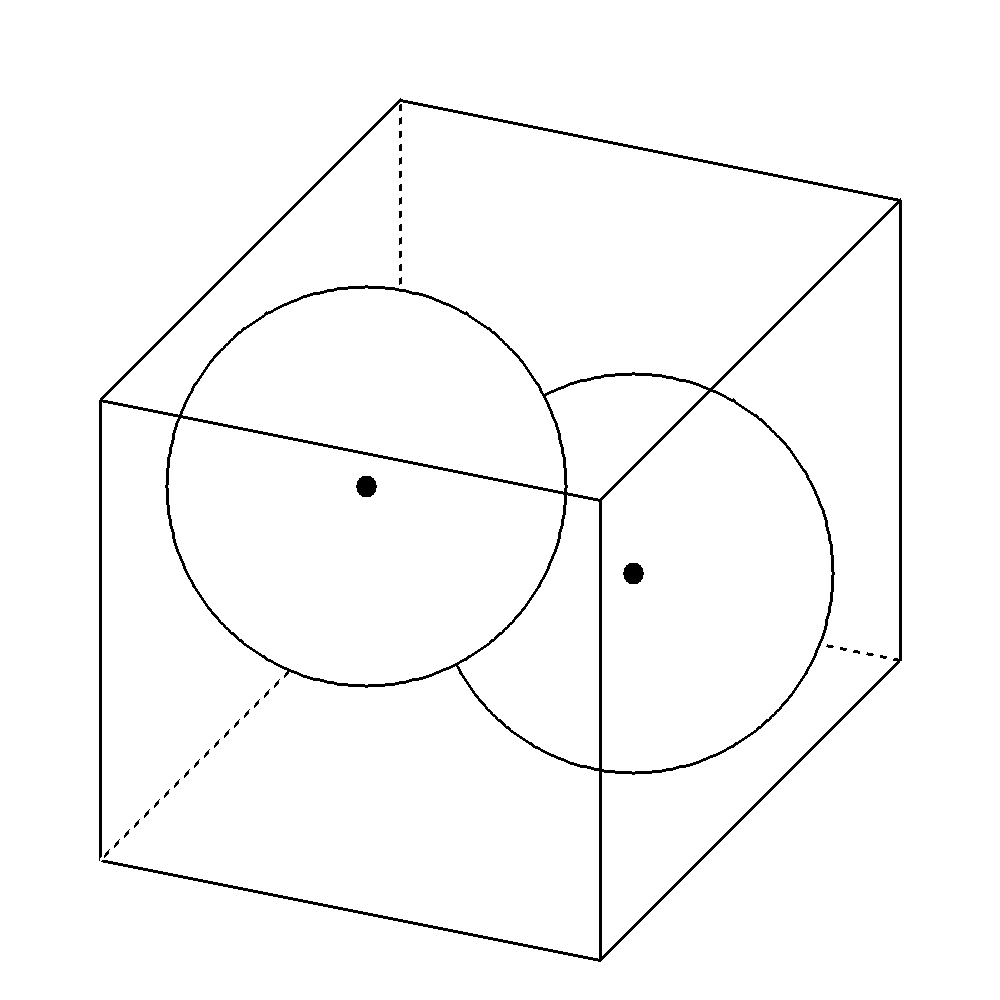
- 次の図のように半径の等しい球が立方体の中に2つ入っている。それぞれの球は立方体の3面と他の球と接している。
立方体の1辺の長さが6cmのとき、球の半径を求めなさい。
-
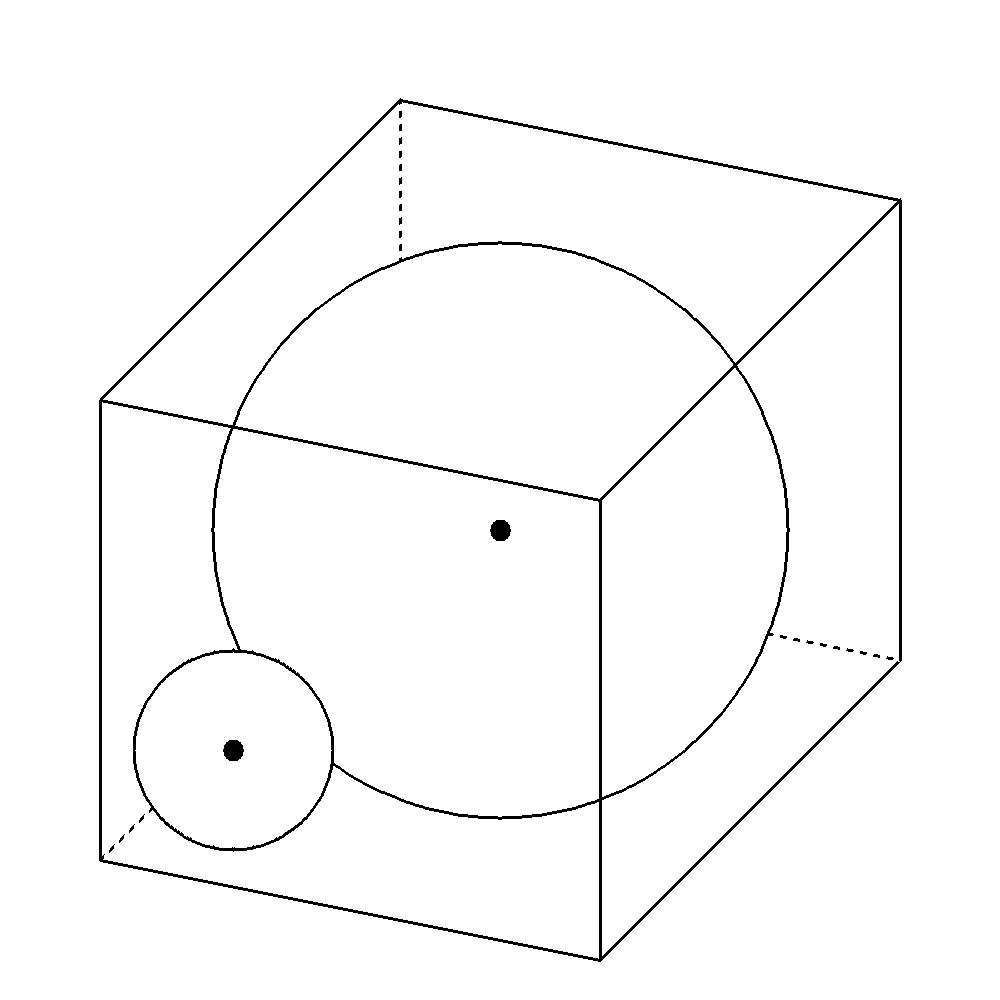
次のように大きな球が一辺\(6cm\)の立方体に内接しており、小さい球は立方体の3面と大きな球に接している。小さい球の半径を求めなさい。
-
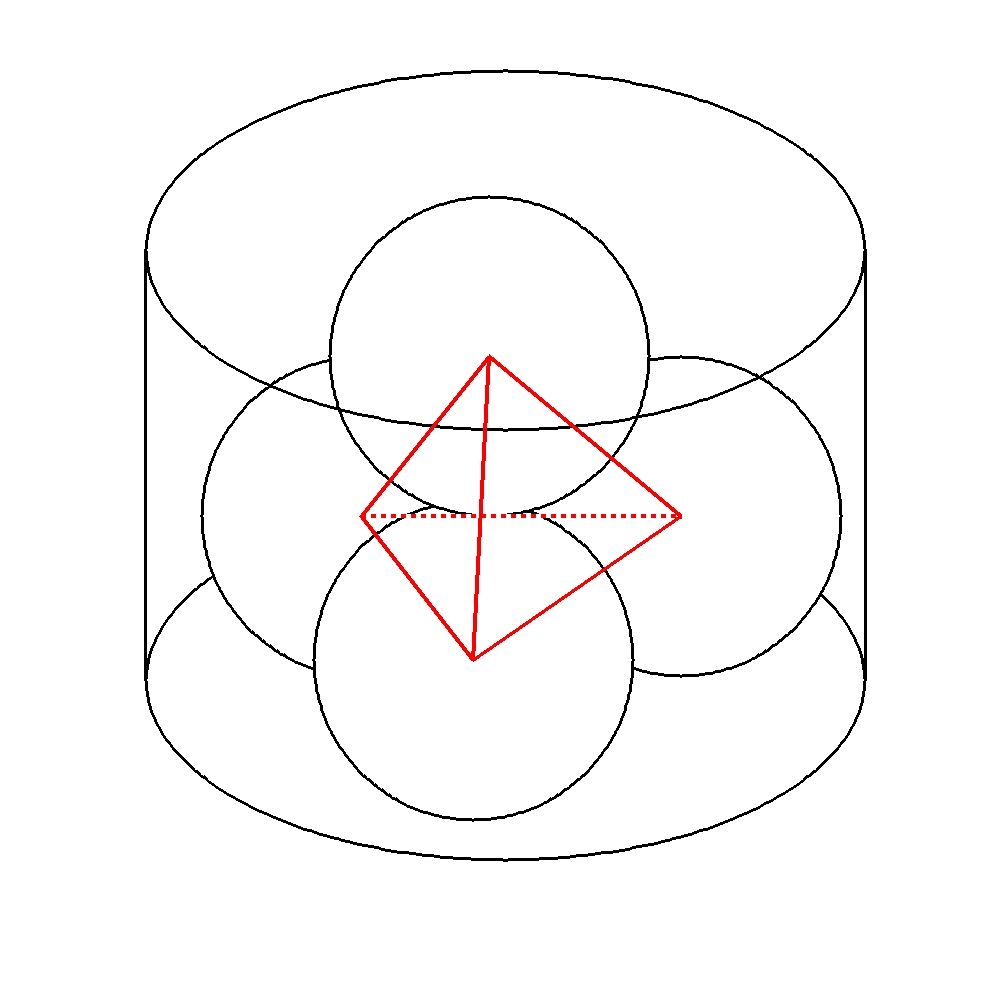
次の図のように円柱の中に3つの球を入れ、その上に1つの球をおく。このとき、下の3つの球は円柱の底面と側面積、および他の球と接している。
上の1つの球は下の3つの球と接している。球の半径が\(1\)のとき円柱の底面の半径を求めなさい。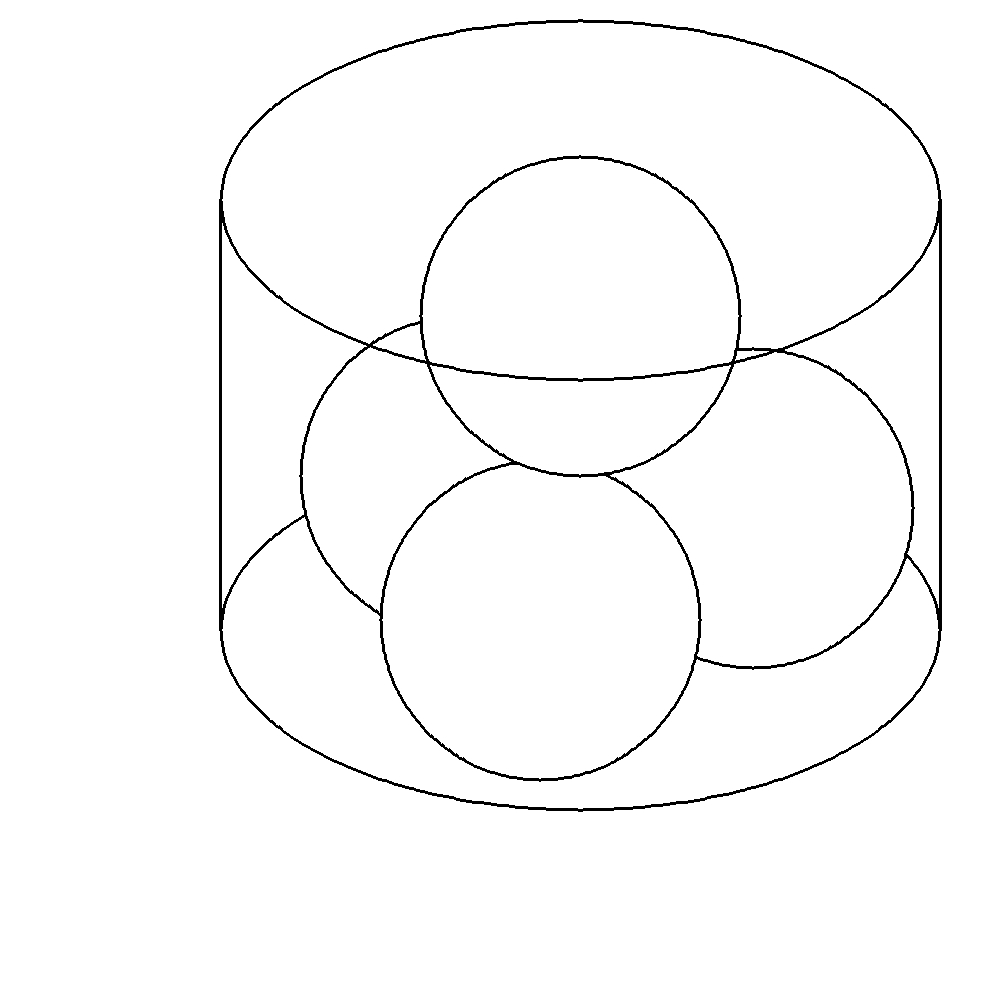
- ③の問題で、上の球の中心と円柱の底面との距離を求めなさい。
- 平面を切り抜け!(他の立体図形の扱い方と同じ)
- 垂直な3面と接している場合→立方体ができる
→角から中心までの距離を求める。
■3面と接するとき
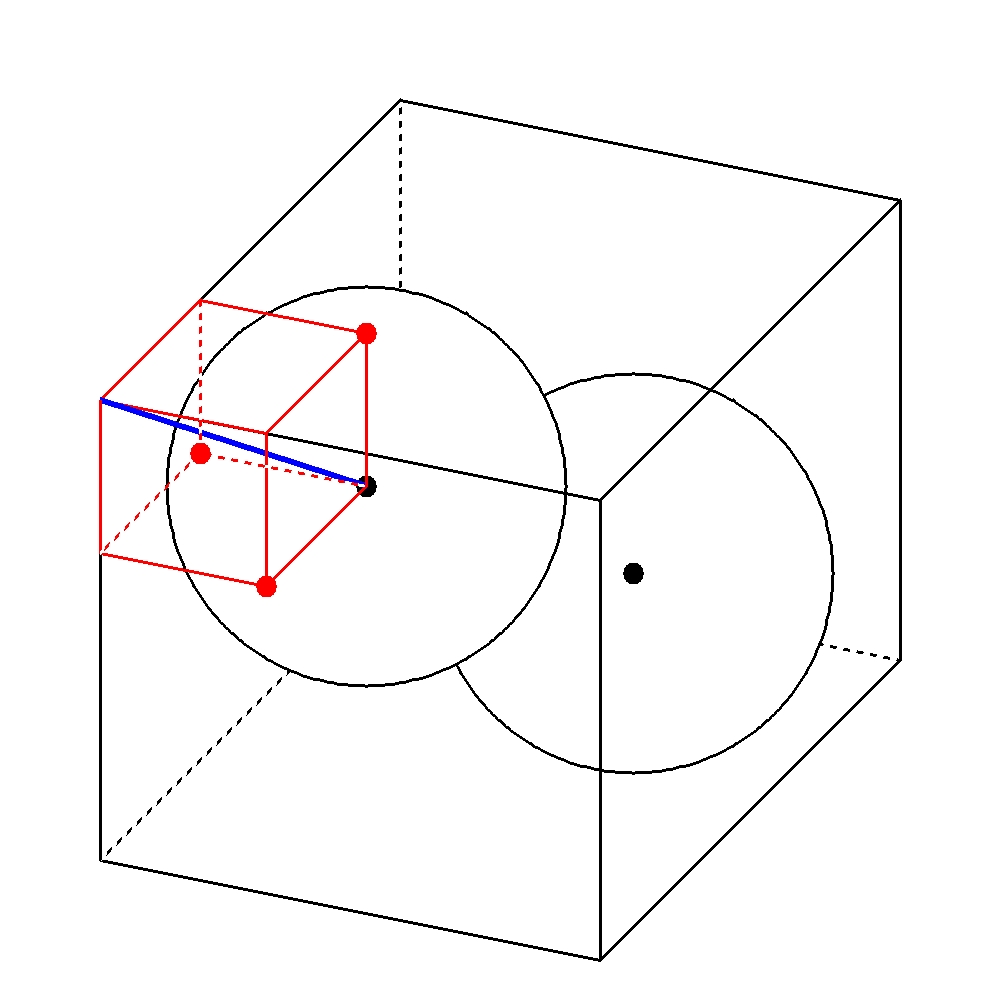
●が球と立方体の接点のとき、球の半径が一辺になる小さな立方体が存在する。
球の半径を\(r\)とするとき、小さな立方体の対角線は\(\sqrt{3}a\)であり、これが立方体の角から球の半径までの距離である。
- 次の図のように半径の等しい球が立方体の中に2つ入っている。それぞれの球は立方体の3面と他の球と接している。
立方体の1辺の長さが6cmのとき、球の半径を求めなさい。 - 次のように大きな球が一辺\(6cm\)の立方体に内接しており、小さい球は立方体の3面と大きな球に接している。小さい球の半径を求めなさい。
-
次の図のように円柱の中に3つの球を入れ、その上に1つの球をおく。このとき、下の3つの球は円柱の底面と側面積、および他の球と接している。
上の1つの球は下の3つの球と接している。球の半径が\(1\)のとき円柱の底面の半径を求めなさい。 - ③の問題で、上の球の中心と円柱の底面との距離を求めなさい。
次の図のように平面で切り抜いて考える。(小さな立方体にも注目しておくこと。)
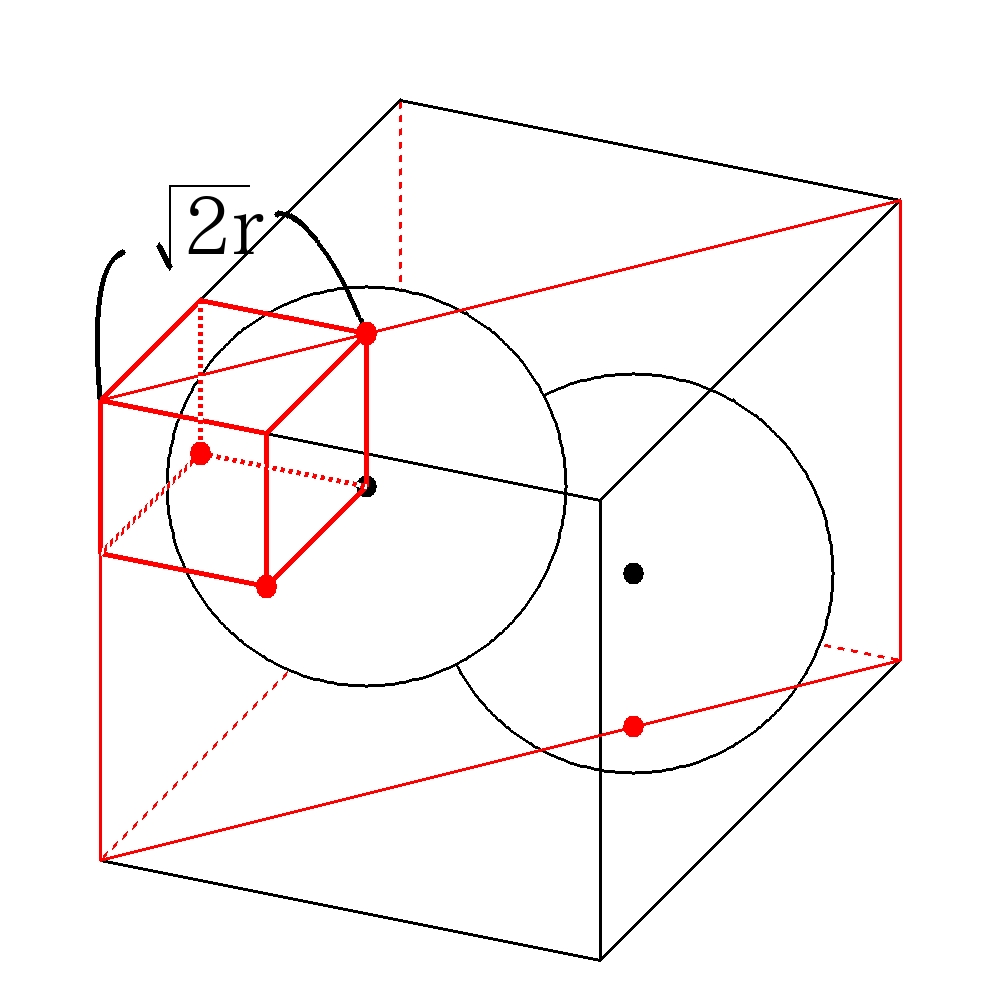
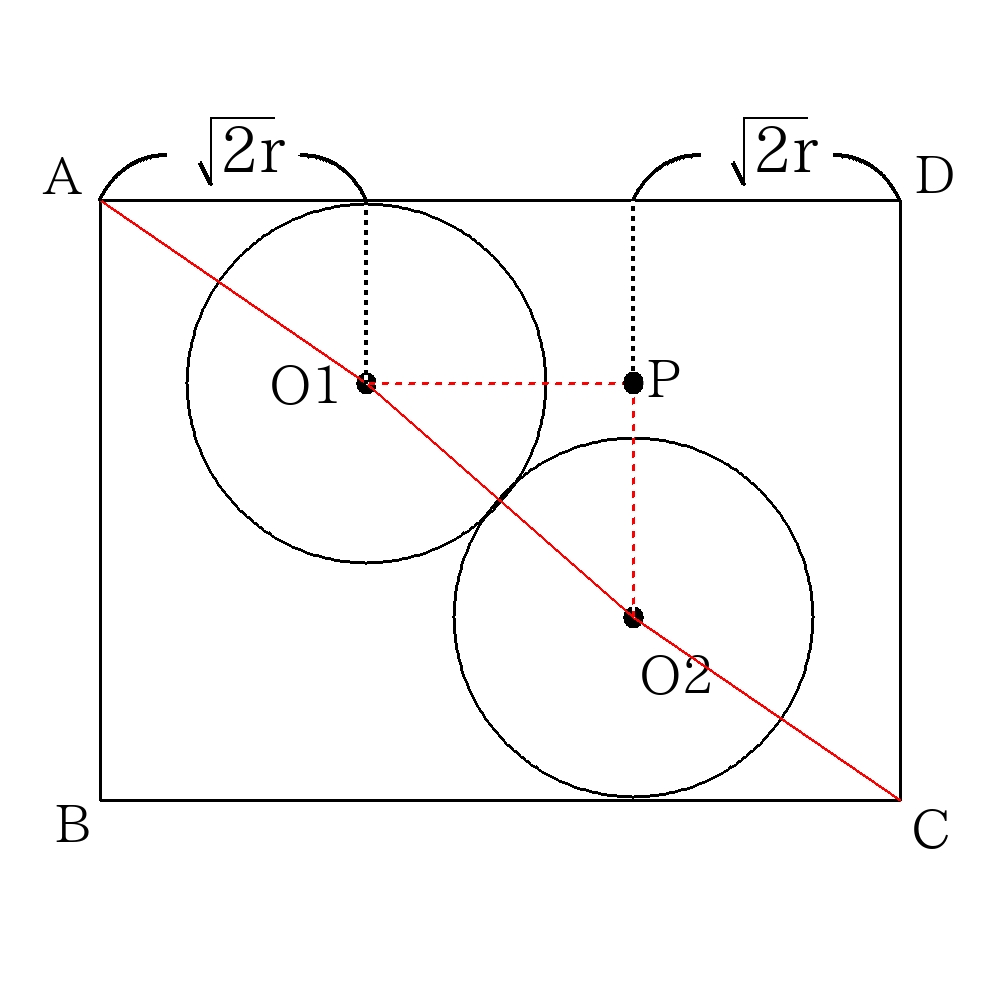
球の半径を\(r\)とする。
\(AO_{1}=CO_{2}=\sqrt{3}r\) ・・・(小さな立方体の対角線)
\(\triangle PO_{1}O_{2} \)で三平方の定理を使うことを目指す。
\(O_{1}O_{2}=2r\)
\(AD\)はもとの立方体の底面の対角線なので、\(AD=6\sqrt{2}\)
\(O_{1}P=AD-2(\sqrt{2}r)=6\sqrt{2}-2\sqrt{2}r\)
\(PO_{2}=6-2r\)
よって、\( \left( 6\sqrt{2}-2\sqrt{2}r \right)^2 + \left( 6-2r \right)^2 = (2r)^2 \)
・・・計算しても良いが、面倒なので、
\( \left( 6\sqrt{2}-2\sqrt{2}r \right) : \left( 6-2r \right)=\sqrt{2}:1 \)であり、その直角三角形の辺の比は\(\sqrt{2}:1:\sqrt{3}\)なので、
\( 1:\sqrt{3}=(6-2r):2r \)
\( \sqrt{3}(6-2r)=2r \)
\( (2+2\sqrt{3})r=6\sqrt{3} \)
\( (1+\sqrt{3})r=3\sqrt{3} \)
\(r= \dfrac{9-3 \sqrt{3}}{2} \)
\(O_{1}O_{}\)を求めるために\(\sqrt{2}:1:\sqrt{3}\)を使ったが、このことから\(O1O2\)は立方体で囲むことができ、その立方体の対角線が\(O_{1}O_{2}\)になることがわかる。
またこのことから\(A,O_{1},O_{2},C\)が一直線上になることもわかる。
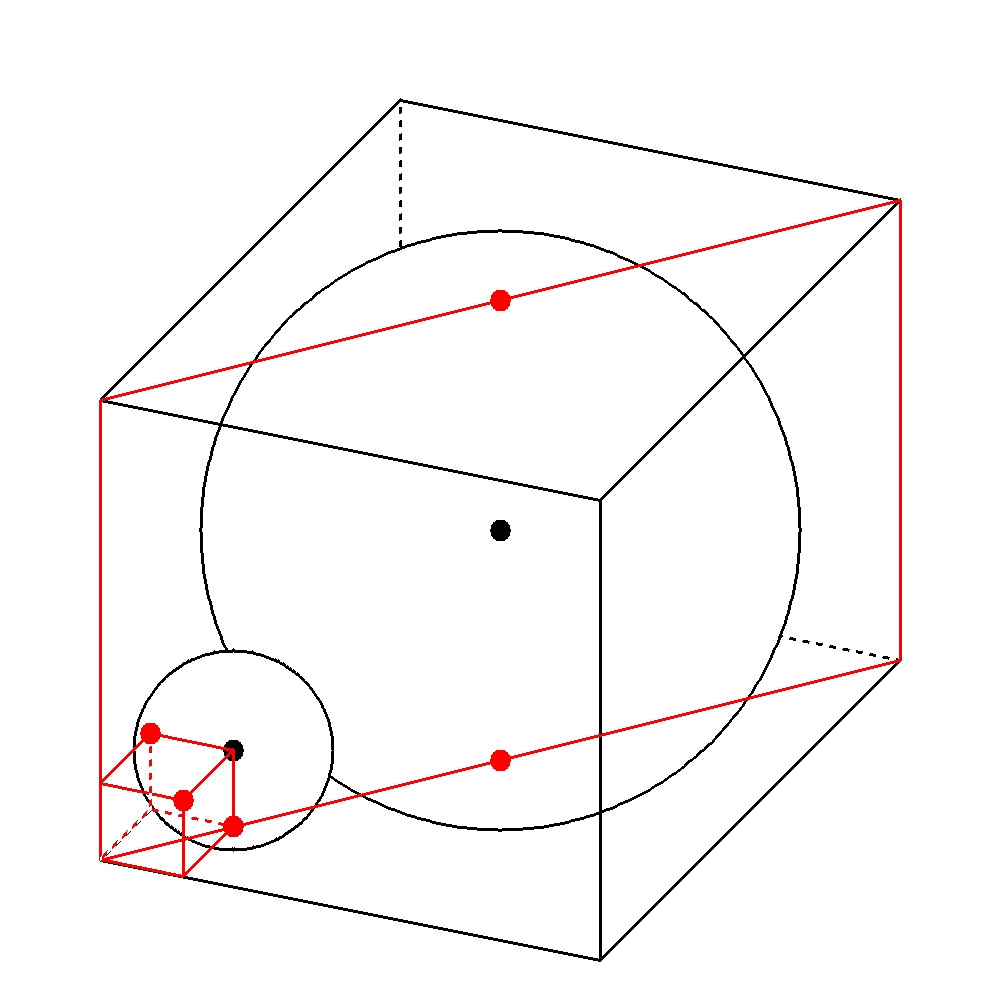
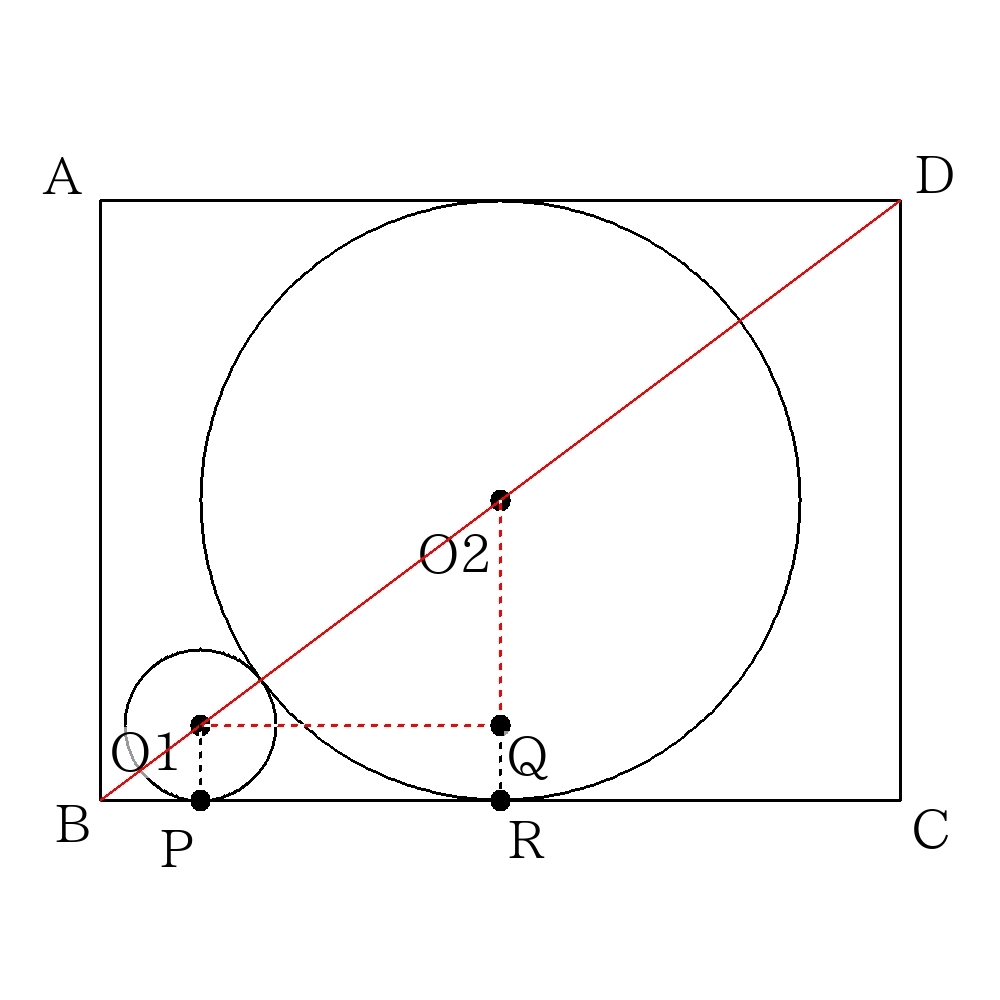
次の図のように平面で切り抜いて考える。(小さな立方体にも注目しておくこと。)
大きな球の半径は\(3cm\)、ここで小さな球の半径を\(rcm\)とおき、
\( \triangle BO_{1}P \)∽\( \triangle O_{1}O_{2}Q \)から計算することを目指す。
\( BO_{1} \)は小さな立方体の対角線なので、\( BO_{1}=\sqrt{3}r \)
\( O_{1}O_{2}=3+r\)、\(O_{1}P=r、O_{2}Q=3-r \)
\( \triangle BO_{1}P \)∽\( \triangle O_{1}O_{2}Q \)より対応する辺の比は等しいので、
\( BO_{1}:O_{1}O_{2}=O_{1}P:O_{2}Q\)
\( \sqrt{3}r:(3+r)=r:(3-r) \)
\( \sqrt{3}r(3-r)=(3+r)r \)
\( \sqrt{3}(3-r)=3+r \)
\( 3\sqrt{3}-\sqrt{3}r=3+r \)
\( (\sqrt{3}+1)r=3\sqrt{3}-3 \)
\( r=\dfrac{3\sqrt{3}-3}{\sqrt{3}+1} \)
\( r=\dfrac{12-6\sqrt{3}}{2} \)
\( r=6-3\sqrt{3} \)
球の中心どうしを結ぶと一辺\(2\)の正四面体になる。
下の3つの球の中心を通るように水平に切断した図を書き抜いて考える。
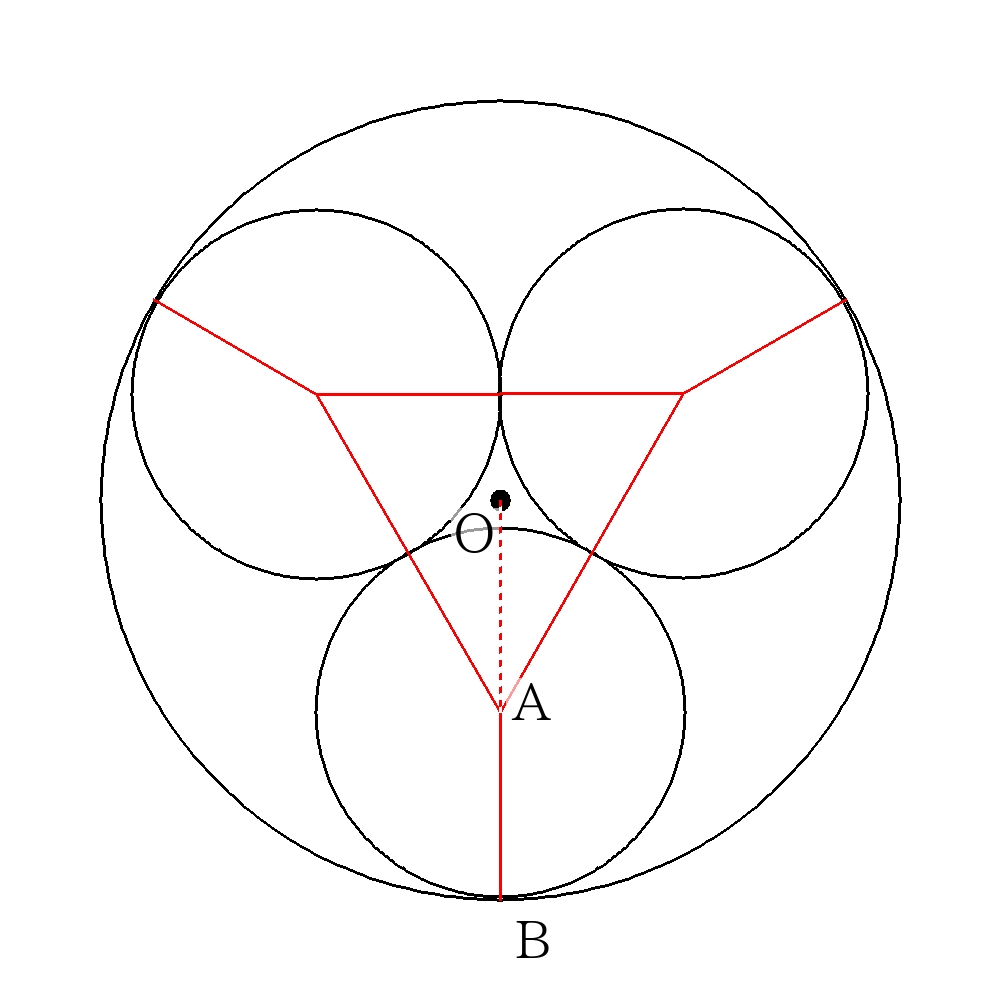
点\(O\)は底面の円の中心であり、小さい円の中心を結んだ三角形の重心である。よって\(OA\)は三角形の高さの\( \dfrac{2}{3} \)なので、
\(OA = \dfrac{\sqrt{3}}{2} \times 2 \times \dfrac{2}{3} = \dfrac{2\sqrt{3}}{3} \)
\(OB\)は底面の円の半径でもあるので
\( r=OB=OA+AB= \dfrac{2\sqrt{3}}{3} + 2 \)
\( r= \dfrac{2\sqrt{3}+6}{3} \)
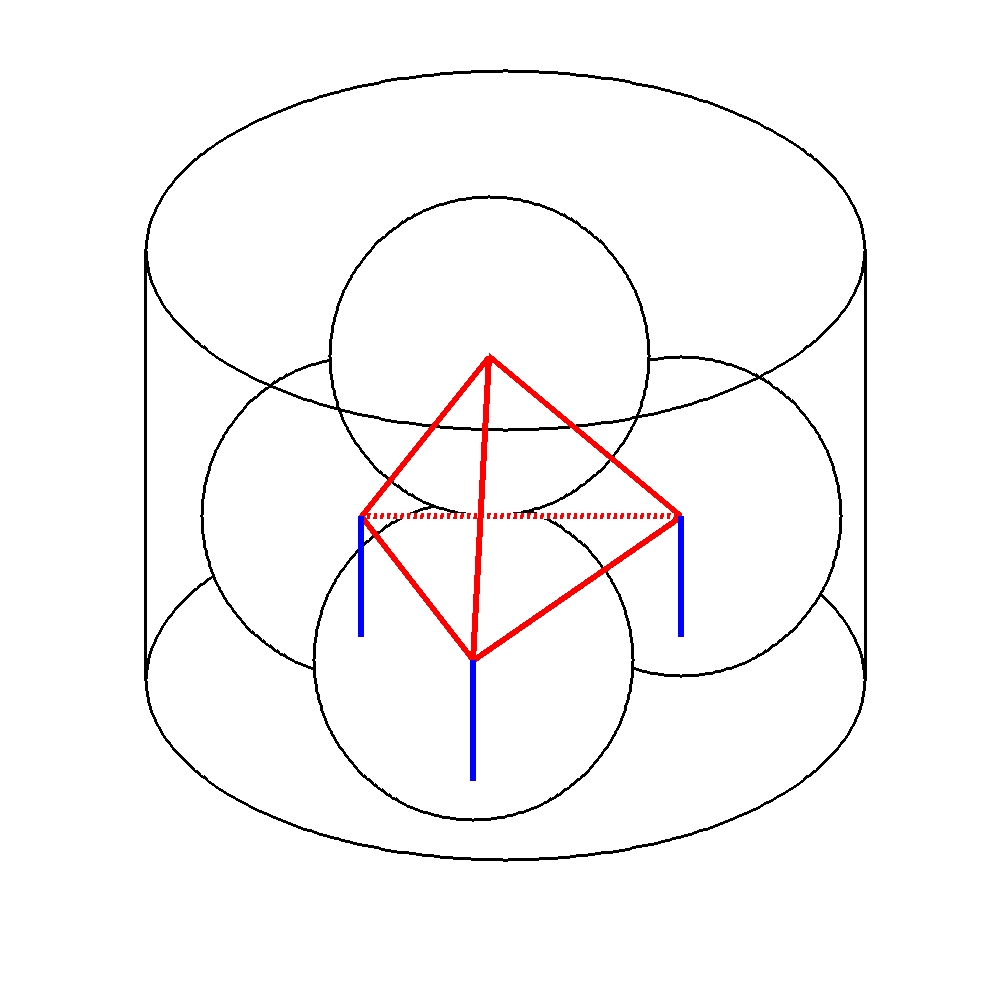
上の球の中心と円柱の底面との距離は、図の正四面体の高さに小球の半径を足したものなので、
\( \dfrac{ \sqrt{6} }{3} \times 2 + 1 \)
\( =\dfrac{ 2\sqrt{6} +3 }{3} \)



コメント