二等辺三角形を見つける
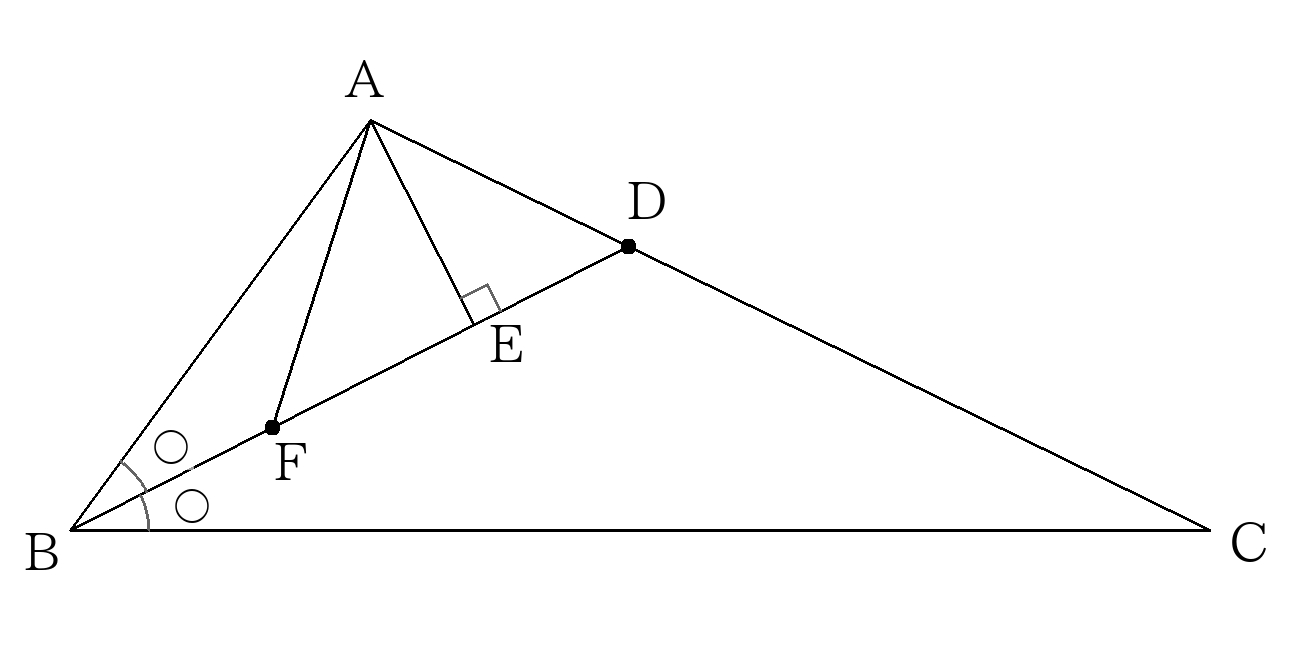
- 次の図のように三角形\(ABC\)があり、\( \angle ABC\)の二等分線と\(AC\)との交点を\(D\)、
\(A\)から\(BD\)に下した垂線を\(AE\)、\(BE\)の中点を\(F\)とする。
\(AB:BC=1:3\)、\(AF=5cm\)のとき\(AC\)の長さを求めなさい。
- 「角の二等分線+垂直=二等辺三角形」
- 「垂直+中点=二等辺三角形」
この2つを疑え!
角の二等分線+垂直=二等辺三角形パターン
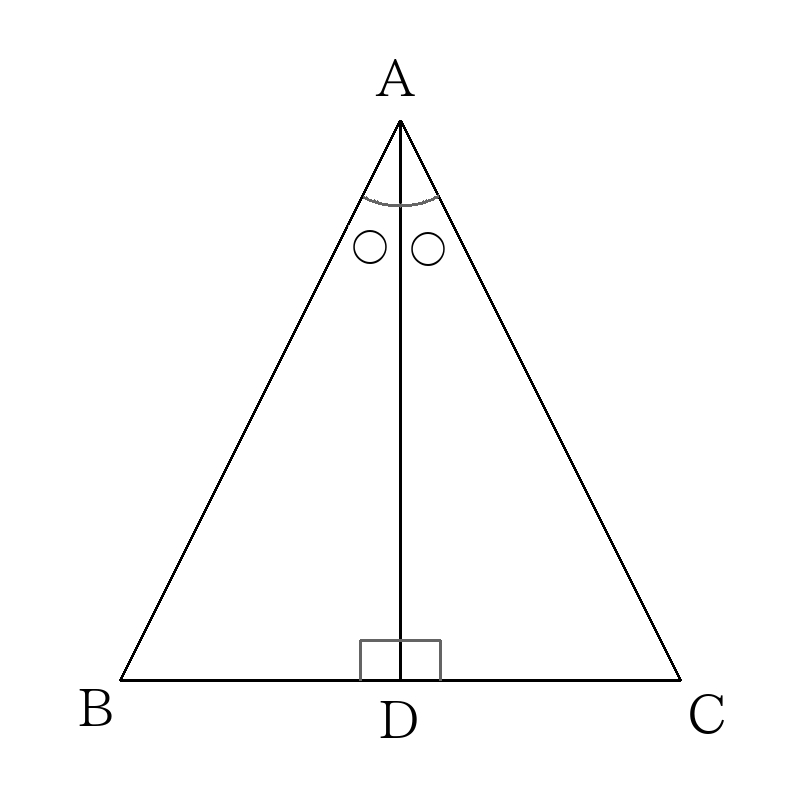
1組の辺とその両端の角がそれぞれ等しいので、\( \triangle ABD ≡ \triangle ACD \)
垂直+中点=二等辺三角形パターン
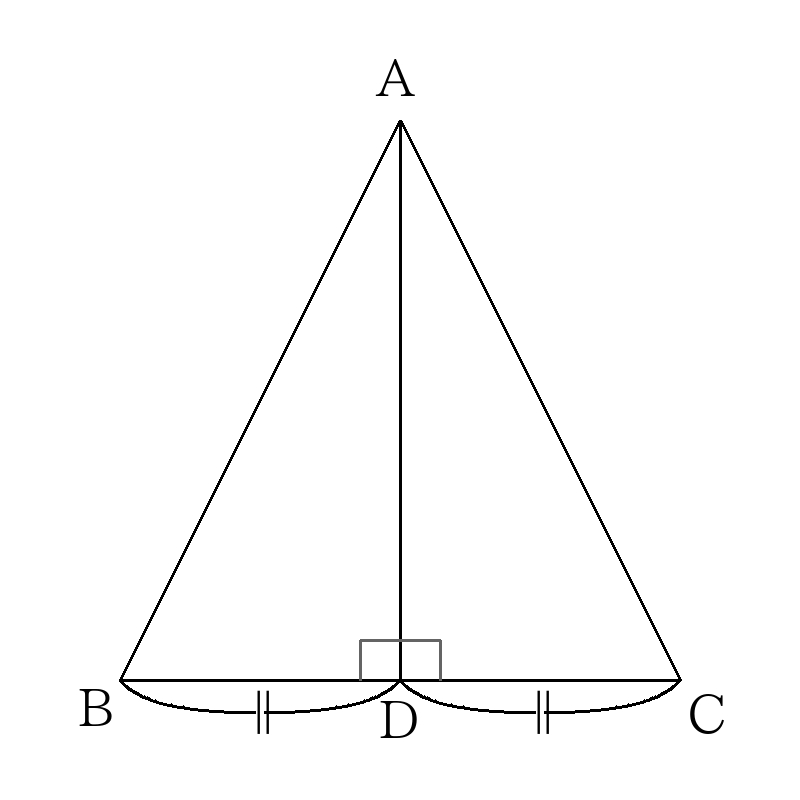
2組の辺とその間の角がそれぞれ等しいので、\( \triangle ABD ≡ \triangle ACD \)
- 次の図のように三角形\(ABC\)があり、\( \angle ABC\)の二等分線と\(AC\)との交点を\(D\)、
\(A\)から\(BD\)に下した垂線を\(AE\)、\(BE\)の中点を\(F\)とする。
\(AB:BC=1:3\)、\(AF=5cm\)のとき\(AC\)の長さを求めなさい。
角の二等分線の定理より、\(AB:BC=AD:DC=1:3\)
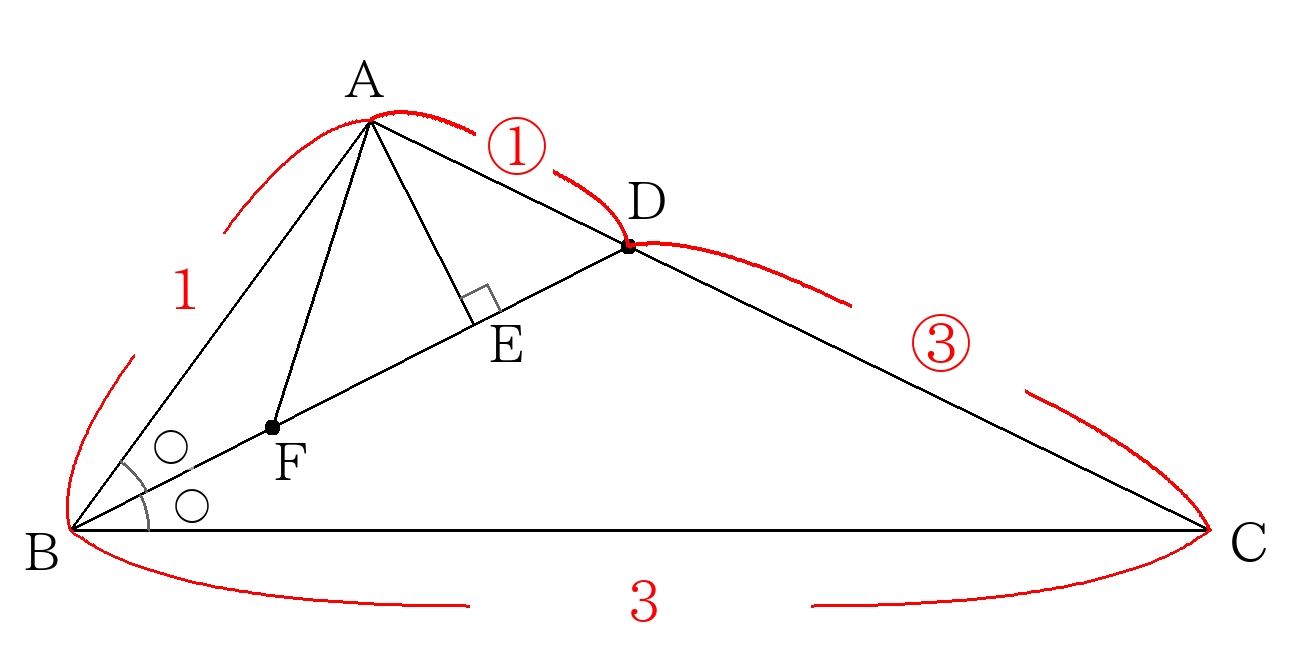
ここで\(AE\)の延長線と\(BC\)との交点を\(G\)とする。
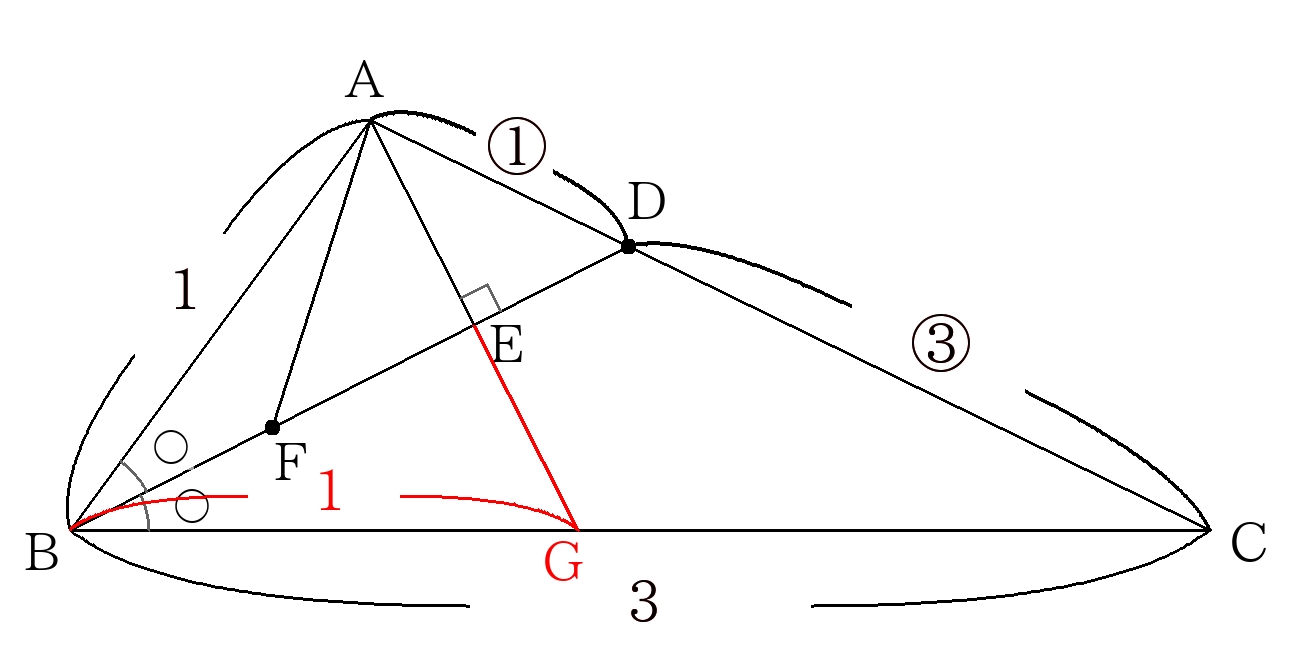
\( \triangle ABG\)において、\( \angle ABG\)のの等分線が\(AG\)と垂直に交わるので、
\( \triangle ABG\)は\(BA=BG\)の二等辺三角形である。
よって、\(BG=1\)、\(GC=2\)となる。
次に\(BE:ED\)をメネラウスの定理によって求める。
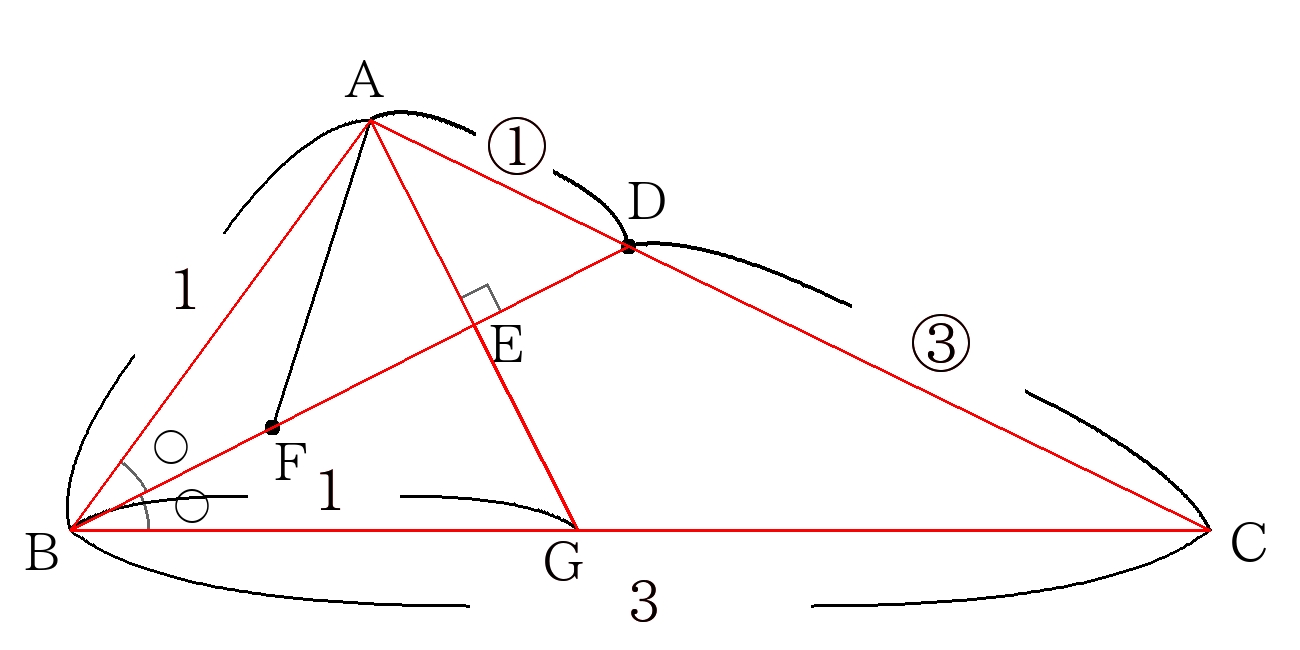
\(
\dfrac{AD}{CA} \times \dfrac{EB}{DE} \times \dfrac{BG}{GC}=1
\)
\(
\dfrac{①}{③+①} \times \dfrac{EB}{DE} \times \dfrac{2}{1}=1
\)
\(
\dfrac{EB}{DE} =2
\)
\(DE:EB=1:2\)
また、点\(F\)は\(BE\)の中点なので、\(BF:FE:ED=1:1:1\)
ここで、\( \triangle ADF\)は頂点\(A\)から\(FD\)に下した垂線が\(FD\)を二等分するので、\(AF=AD\)の二等辺三角形である。
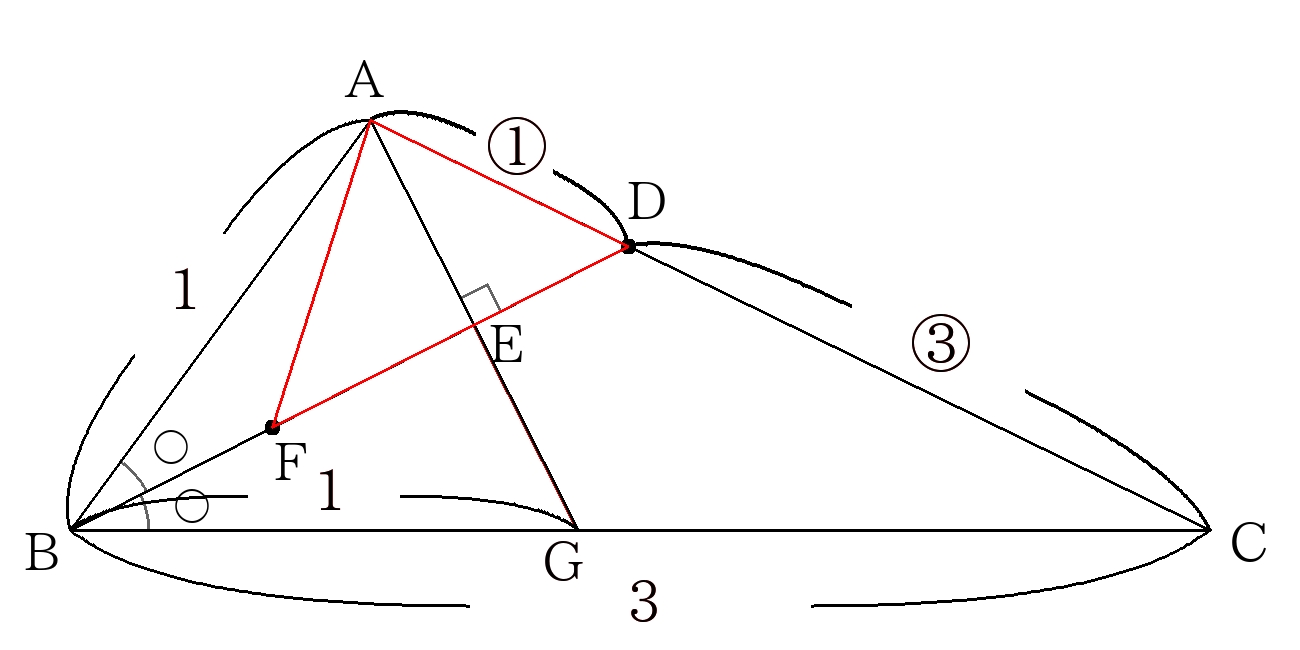
よって、\(AD=AD=5cm\)
\(AD:DC=1:3\)より、
\( AC= 5 \times \dfrac{1+3}{1}=20\)
\(AC=20cm \)



コメント