黄金比
- 次の図のような長方形\(ABCD\)と正方形\(ABFE\)があり、長方形\(FCDE\)は長方形\(ABCD\)と相似である。
\(AB:BC\)の比を求めなさい。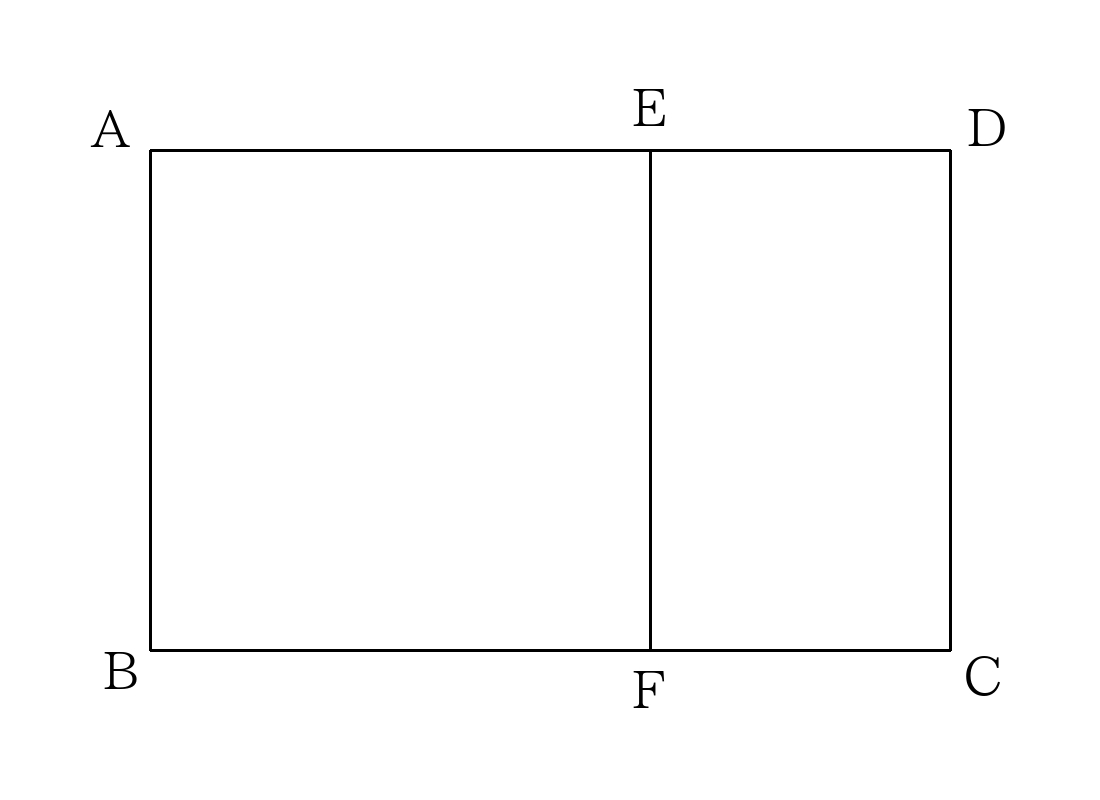
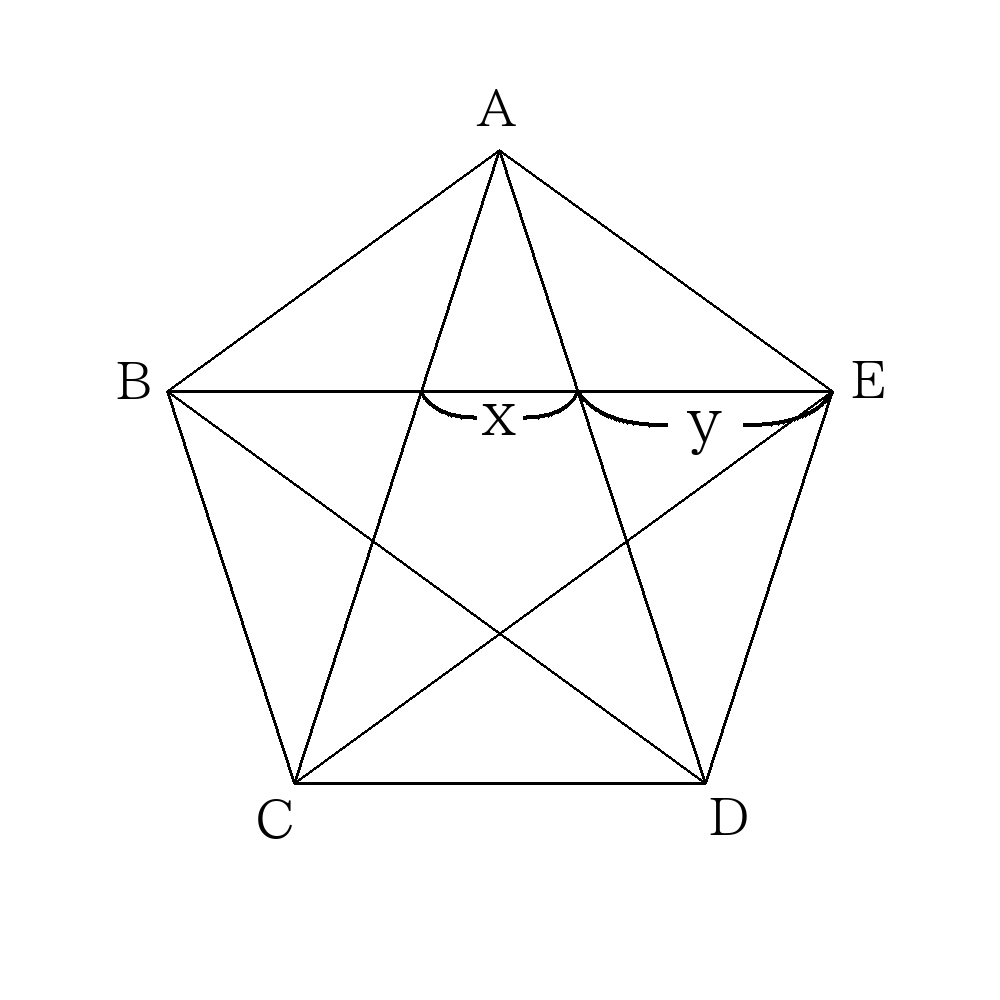
- 次の図のように1辺の長さが\(2cm\)の正五角形があり、対角線を結ぶ。
このとき、\(x,y\)の長さをそれぞれ求めなさい。
- 18°の倍数→黄金比を疑え!
\( \dfrac{1+\sqrt{5}}{2} \)を黄金数、\( 1:\dfrac{1+\sqrt{5}}{2} \)を黄金比とよぶ。
今回の問題は代表的な黄金比の問題なので、解きながら理解を深めること。
- 次の図のような長方形\(ABCD\)と正方形\(ABFE\)があり、長方形\(FCDE\)は長方形\(ABCD\)と相似である。
\(AB:BC\)の比を求めなさい。 - 次の図のように1辺の長さが\(2cm\)の正五角形があり、対角線を結ぶ。
このとき、\(x,y\)の長さをそれぞれ求めなさい。
\(AB=AE=1\)、\(ED=x\)とする
![]()
長方形\(FCDE\)∽長方形\(ABCD\)より対応する辺の比は等しいので、
\(AB:AD=FC:FE\)
\(1:(1+x)=x:1\)
外項の積と内項の積が等しいので、
\(1=x(1+x)\)
\(x^2+x-1=0\)
\( x=\dfrac{-1 \pm \sqrt{5}}{2} \)
\(x>0\)より
\( x=\dfrac{-1 + \sqrt{5}}{2} \)
よって
\(AB:BC=1:(1+x)=1:\dfrac{1 + \sqrt{5}}{2}\)
\(AB:BC=1: \dfrac{1+ \sqrt{5}}{2}\)
\( \triangle ABE\)に注目する。対角線の交点を図のように\(F,G\)とし、二等辺三角形の関係から角度を書き入れる。
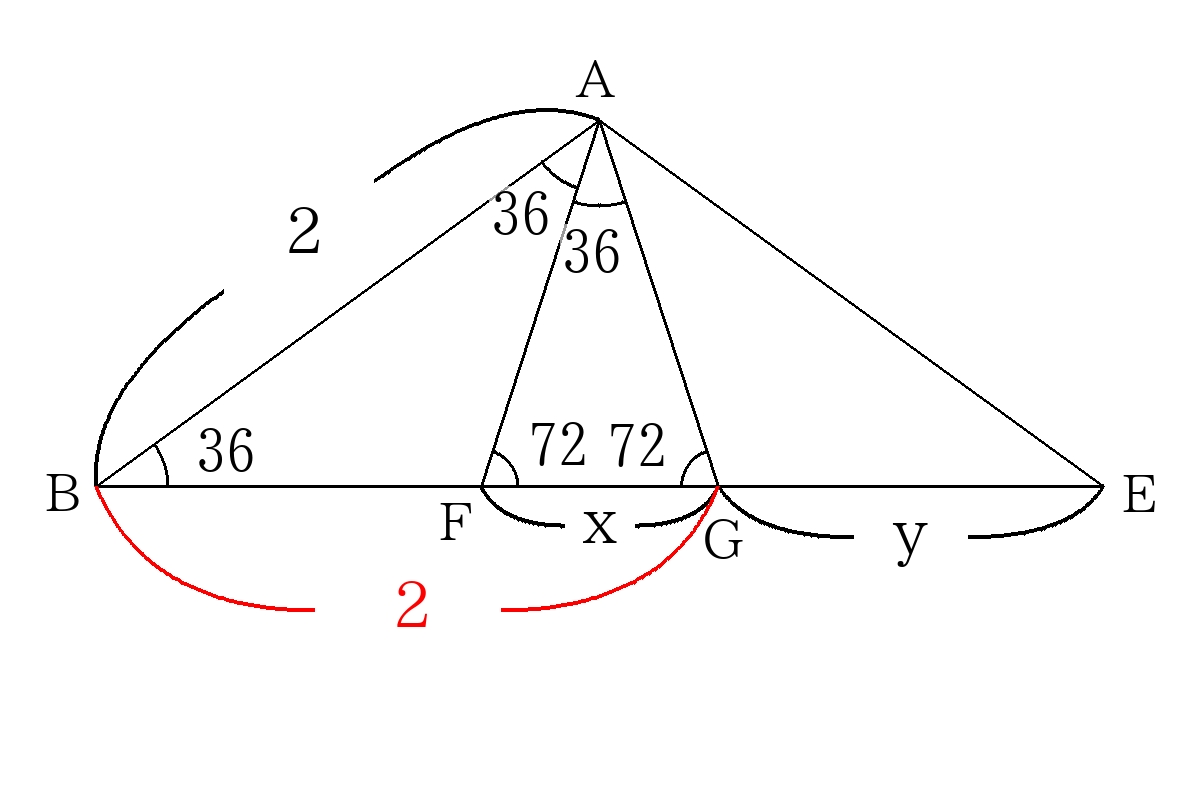
\( \triangle ABG \)∽\( \triangle FAG \)を使って計算することを目指す。
二等辺三角形より、\(BG=BA=2cm\)
\( BF=BG-GF=2-x \)
二等辺三角形より、\( FA=FB=2-x \)
二等辺三角形より、\( AG=AF=2-x \)
\( \triangle ABG \)∽\( \triangle FAG \)より対応する辺の比は等しいので、
\( AB:FA=AG:FG \)
\( 2:(2-x)=(2-x):x\)
外項の積と内項の積は等しいので、
\( 2x=(2-x)^2 \)
\( x=3 \pm \sqrt{5} \)
ここで、\( x \lt 2\)なので、
\( x=3 – \sqrt{5} \)
\(y=2-x=2-\left( 3 – \sqrt{5} \right) = \sqrt{5} -1 \)
\(x=3- \sqrt{5},y= \sqrt{5}-1 \)
※五角形には黄金比が存在する。
\(FG:AF=x:y=\left( 3 – \sqrt{5} \right):\left( \sqrt{5} -1 \right) \)
比を簡単にするために比の両方に\(\left( 3 + \sqrt{5} \right)\)をかけると
\( 4:\left( 2 + 2\sqrt{5} \right) \)
4で割って
\( 1 :\dfrac{ 1 + \sqrt{5} }{2} \dots 黄金比\)
図の正五角形において\(AF:AB\)も黄金比になる。
なお黄金比の表し方を変えるために比の両方に\(\left( 1 – \sqrt{5} \right)\)をかけると
\(1 :\dfrac{ 1 + \sqrt{5} }{2}=\left( 1 – \sqrt{5} \right) : 2 \)
2で割って
\(\dfrac{ 1 – \sqrt{5} }{2} : 1 \)となる。比のとり方を逆にしただけで、これも黄金比であることを知っておくと戸惑わない。
また、ここまでの計算で、
\(\dfrac{ 1 – \sqrt{5} }{2}=\dfrac{ 1 + \sqrt{5} }{2}-1=1 \div \dfrac{ 1 + \sqrt{5} }{2} \)
となり、黄金比は興味深い数であることがわかる。



コメント