直交条件
放物線\(m:y=\dfrac{1}{2}a^2 x^2\)と直線\(ℓ:y=ax+4\)があり、点\(A\)、\(B\)で交わっている。これについて次の問に答えなさい。
ただし\(a>0\)とする。
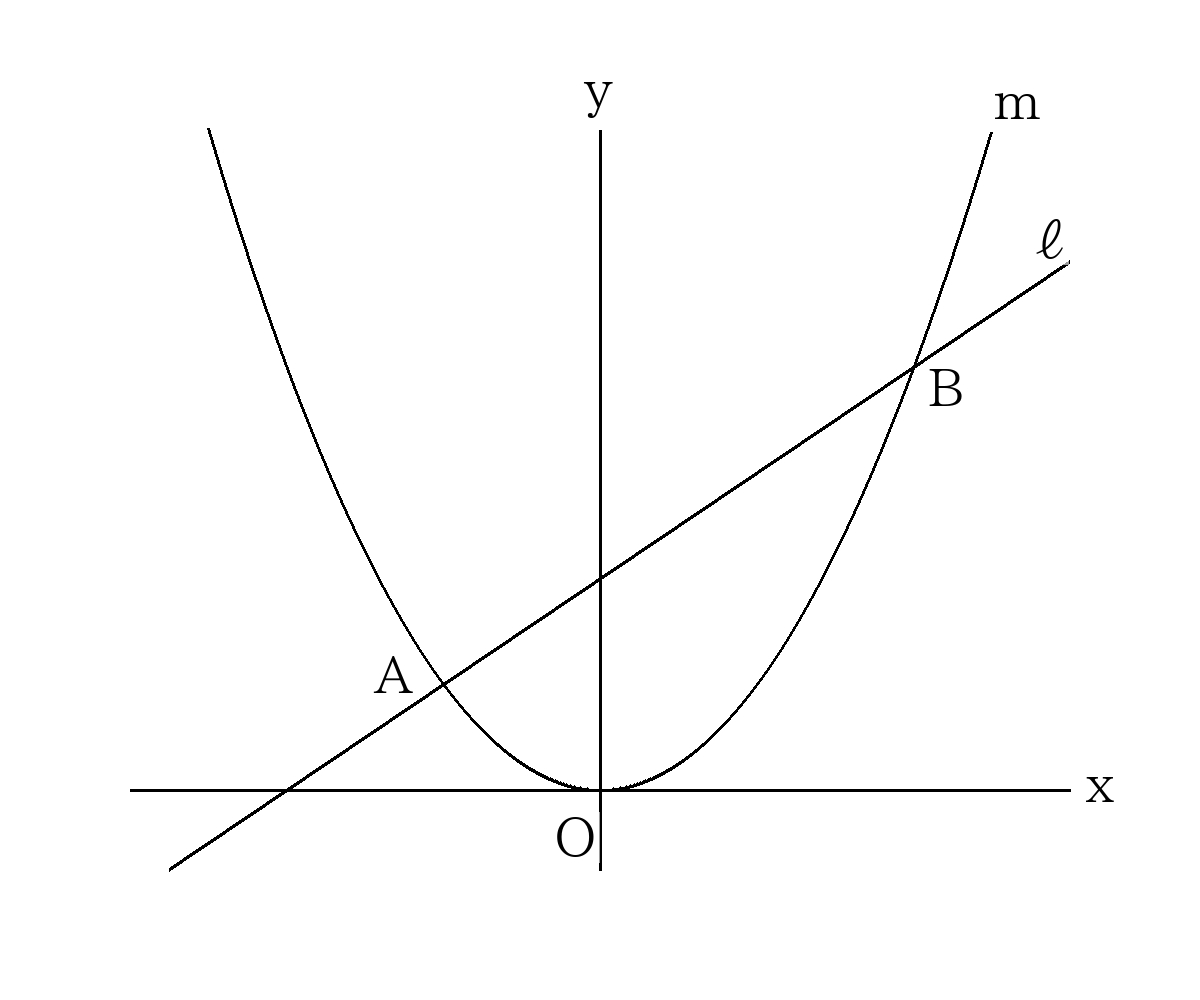
- 交点\(a\),\(b\)の座標を表しなさい。ただし\(a\)を用いても良いものとする。
- \(y\)軸上に点\(C(0,12)\)があり、直線\(AC\)と直線\(BC\)は直角に交わる。このとき\(a\)の値を求めなさい。
- 線分\(AB\)を直径とする円を書き、原点\(O\)が円周上にくるとき、\(a\)の値を求めなさい。
- 2直線\(y=ax+b\)と\(y=cx+d\)が直角に交わるとき、次の関係が成り立つ。
\(a \times c=-1\)
(傾きの積が\(-1\))
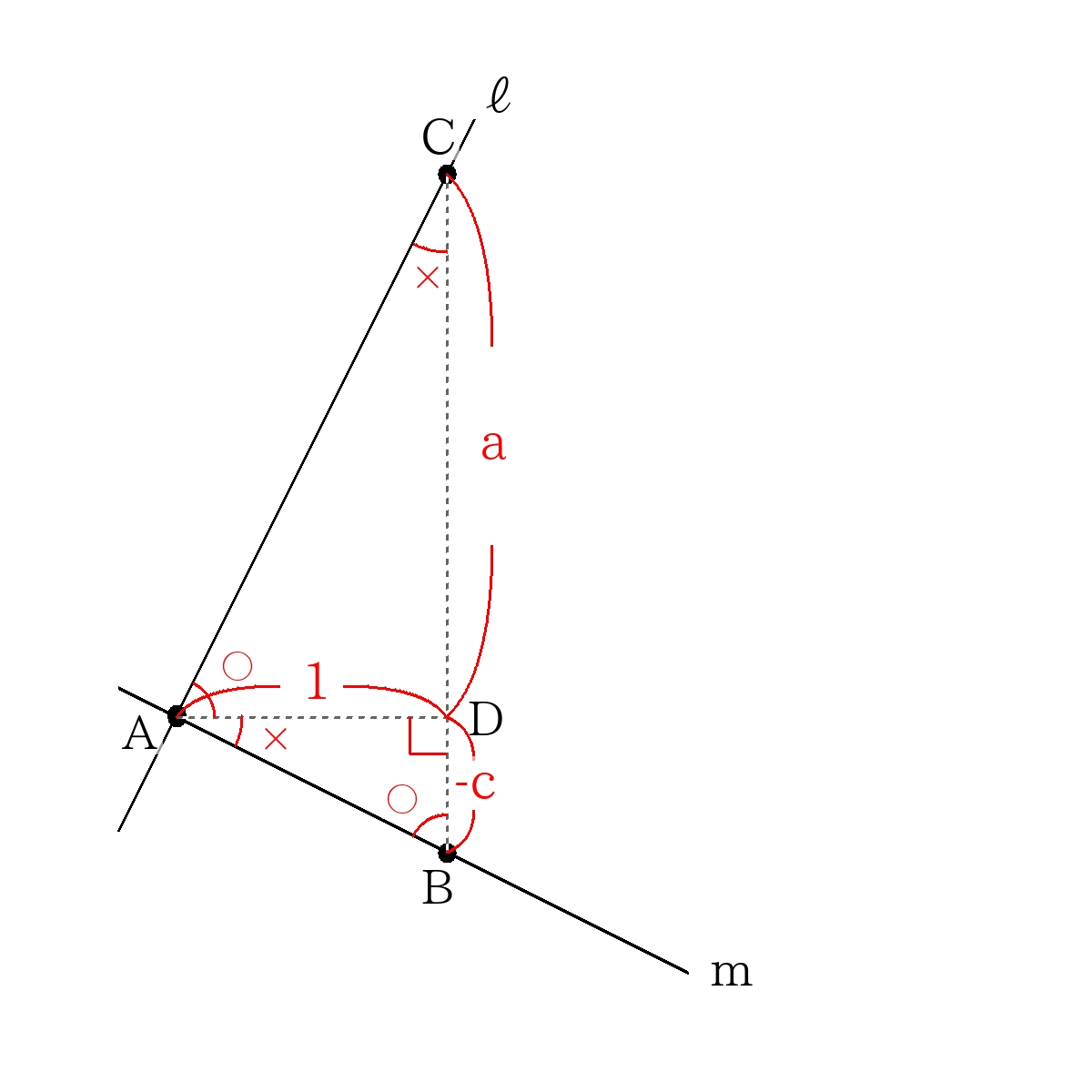
図において直線\(ℓ\)が\(y=ax+b\)、直線\(m\)が\(y=cx+d\)のとき、傾きの関係からそれぞれの長さを書き入れる。
※\(c< 0 \)より\(DB\)の長さが\(-c\)になることに注意。
角度の関係を書き入れると、\( \triangle ADC \) ∽ \( \triangle BDA \)になる。
相似の図形の対応する辺の比は等しいので、
\(AD:DC=BD:DA\)
\(1:a=(-c):1\)
内項の積と外項の積は等しいので、
\( a \times (-c)=1 \)
\( a \times c = -1 \)
- 放物線\(m:y=\dfrac{1}{2}a^2 x^2\)と直線\(ℓ:y=ax+4\)があり、点\(A\)、\(B\)で交わっている。これについて次の問に答えなさい。
- 交点\(a\),\(b\)の座標を表しなさい。ただし\(a\)を用いても良いものとする。
- \(y\)軸上に点\(C(0,12)\)があり、直線\(AC\)と直線\(BC\)は直角に交わる。このとき\(a\)の値を求めなさい。
- 線分\(AB\)を直径とする円を書き、原点\(O\)が円周上にくるとき、\(a\)の値を求めなさい。
ただし\(a>0\)とする。

\(y=\dfrac{1}{2}a^2 x^2\)、\(y=ax+4\)を連立すると、
\(\dfrac{1}{2}a^2 x^2=ax+4\)
\(a^2 x^2=2ax+8\)
\(a^2 x^2-2ax-8=0\)
\((ax-4)(ax+2)=0\)
\(x=\dfrac{4}{a},-\dfrac{2}{a}\)
\(y\)座標は\(y=ax+4\)に代入して計算すれば良い。
\(A \left(- \dfrac{2}{a},2 \right),B \left( \dfrac{4}{a},8 \right) \)
\(y=ax+4\)を\(x\)について解き、\(y=\dfrac{1}{2}a^2 x^2\)に代入して\(y\)から求めても良い。
\(A \left(-\dfrac{2}{a},6 \right),B \left( \dfrac{4}{a},8 \right),C(0,12)\)があり、直線\(AC\)と直線\(BC\)の傾きの積が\(-1\)になれば良い。
※今回、\(x\)の増加量が分数になるため(傾き)=(yの増加量)÷(xの増加量)で計算する。
\(AC\)の傾きは
\( \left( 12-6 \right) \div \left( 0- \left(-\dfrac{2}{a} \right) \right) \)
\(=6 \div \dfrac{2}{a}=3a \)
\(BC\)の傾きは
\( \left( 12-8 \right) \div \left( 0- \dfrac{4}{a} \right) \)
\(=4 \div \dfrac{4}{a}=-a \)
傾きの積が\(-1\)なので、
\(3a \times (-a)=-1 \)
\(a^2= \dfrac{1}{3}\)
\(a>0\)より
\(a=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
\(a= \dfrac{ \sqrt{3}}{3} \)
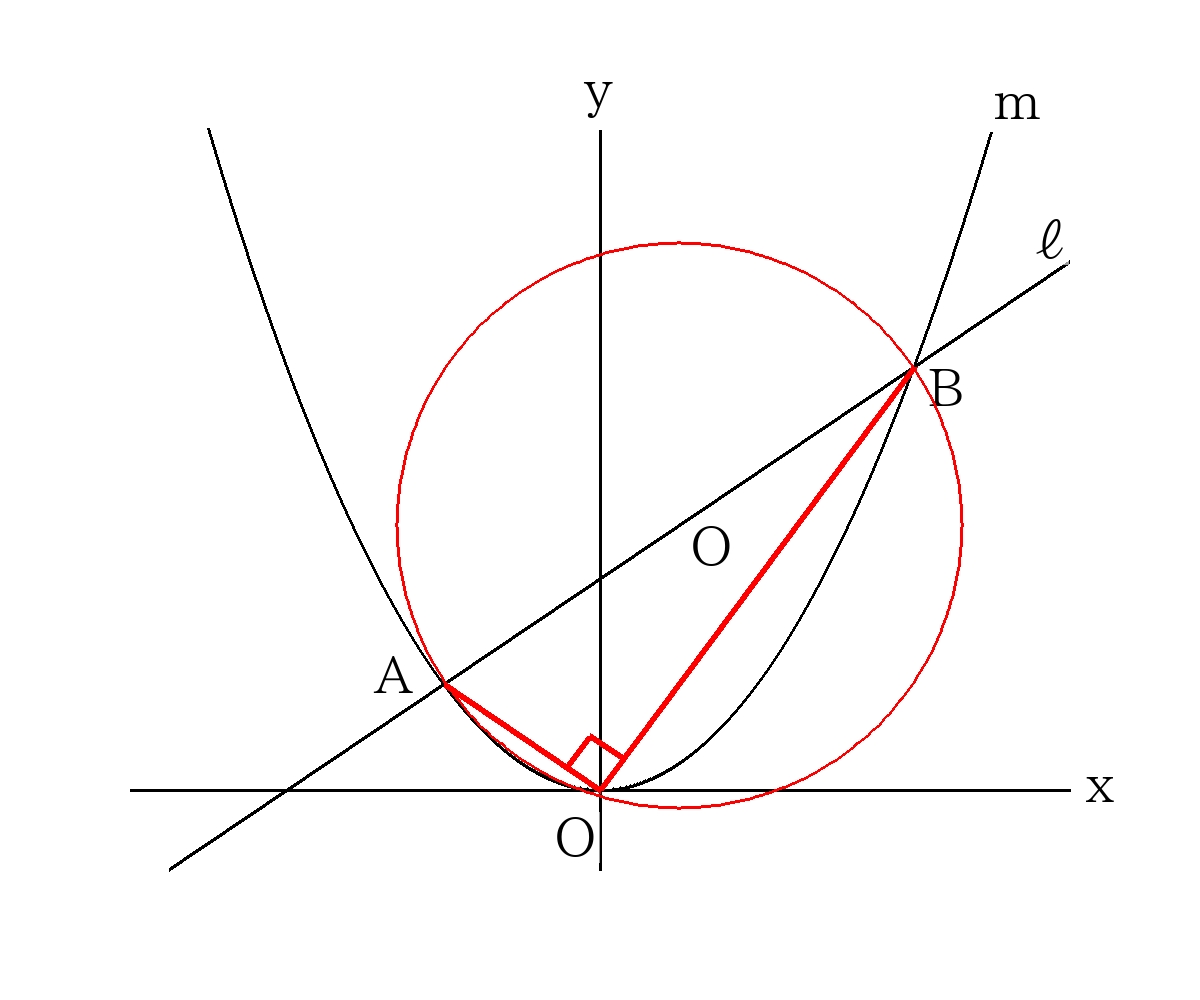
\(AB\)を直径とする円を書いたとき、円周角の定理より\( \angle AOB=90° \)になる。
よって、直線\(AO\)と直線\(BO\)が垂直に交わるように計算すれば良い。
①より、\( A \left(-\dfrac{2}{a},2 \right),B \left( \dfrac{4}{a},8 \right) \)なので、
\( \dfrac{2-0}{\left( -\dfrac{2}{a} \right)-0} \times \dfrac{8-0}{\left( -\dfrac{4}{a} \right)-0} =-1 \)
※増加量から式を立てたが、比例の式から求めても良い。
※分母に分数がくる分数は、\(\dfrac{Y}{X}=Y \div X\)のようにわり算で計算処理すること。
\( -a \times 2a =-1 \)
\(a>0\)より
\(a= \dfrac{1}{ \sqrt{2}}= \dfrac{ \sqrt{2}}{2} \)



コメント