垂線の長さ
面積体積からの逆算
例題
次の図のような直方体\(ABCD-EFGH\)がある。これについて次の問いに答えなさい。
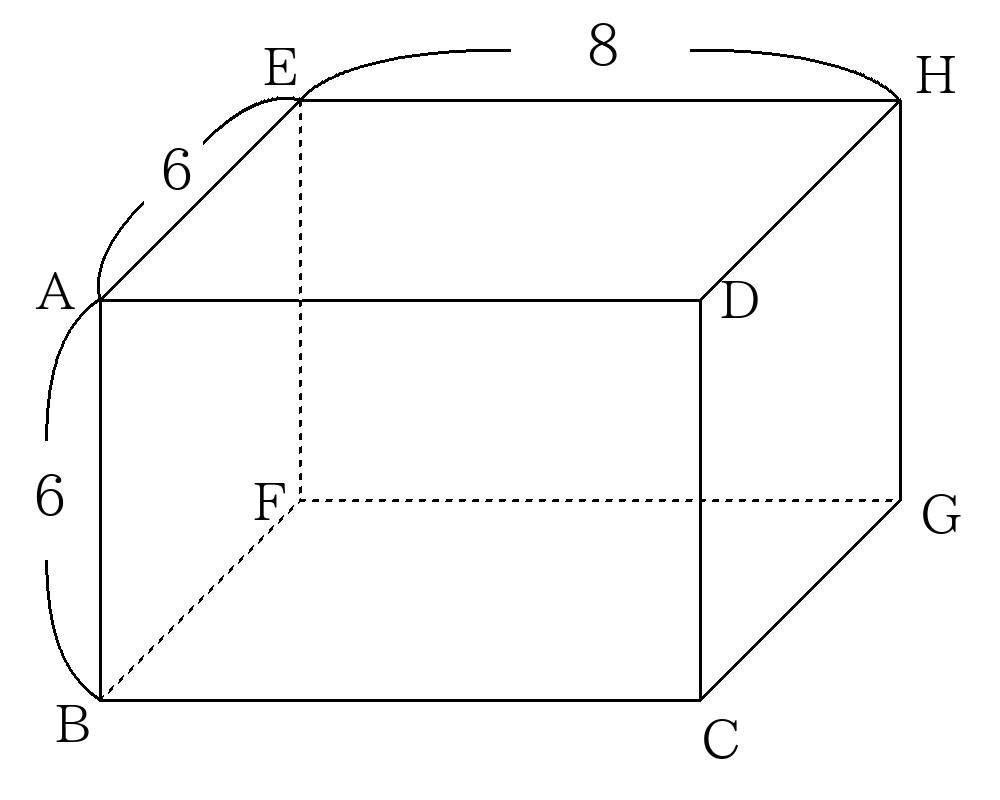
- 頂点\(A\)から線分\(EC\)に下ろした垂線の長さを求めなさい。
- 頂点\(D\)から面\(ACH\)に下ろした垂線の長さを求めなさい。
まずはこう解け!
- 面積や体積からの逆算を考えろ!
解答
- 頂点\(A\)から線分\(EC\)に下ろした垂線の長さを求めなさい。
- 頂点\(D\)から面\(ACH\)に下ろした垂線の長さを求めなさい。
頂点\(A\)から線分\(EC\)に下ろした垂線を\(AI\)として図示する。
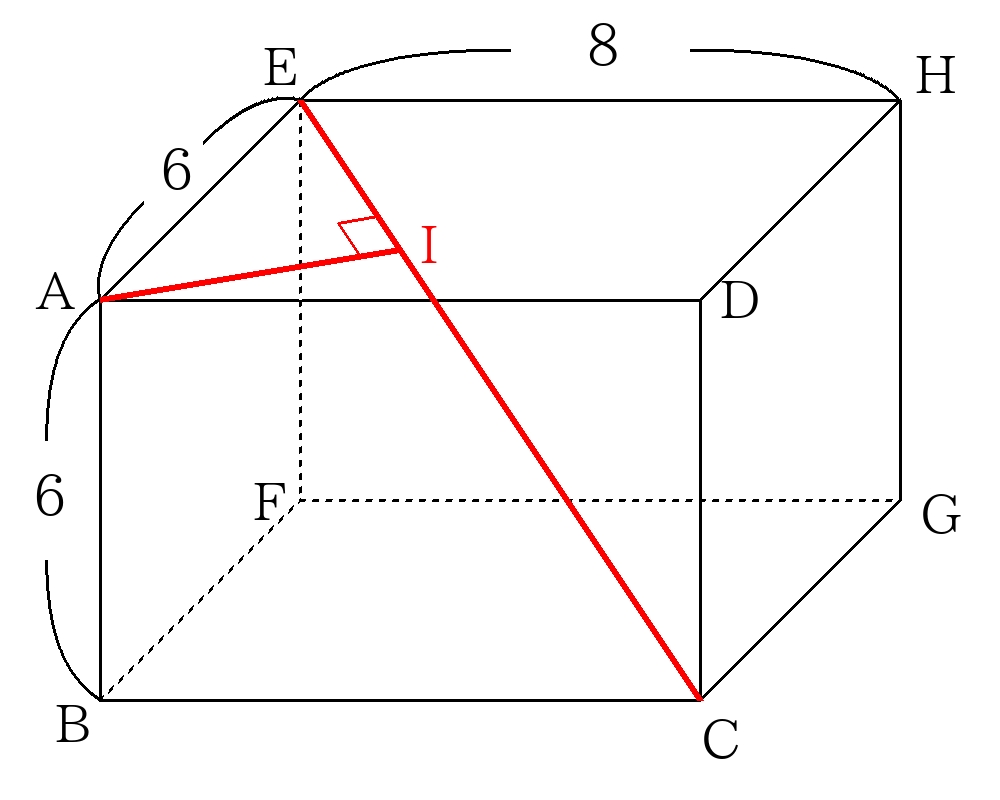
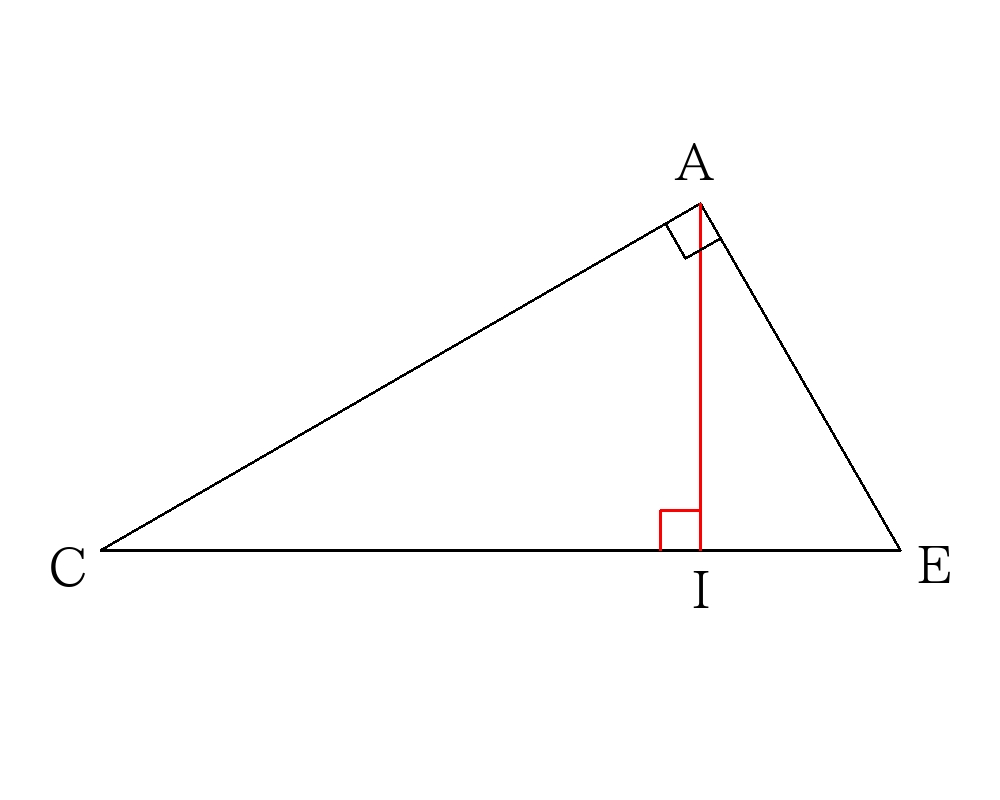
垂線\(AI\)は直角三角形\(ACE\)の面積より逆算すれば良い。
\(AC= \sqrt{6^2+8^2}=10 \)
\(EC= \sqrt{6^2+10^2}=2 \sqrt{34} \)
\(\triangle ACE\)の面積より
\(2 \sqrt{34} \times AI \times \dfrac{1}{2}=6 \times 10 \times \dfrac{1}{2} \)
\(AI= \dfrac{15 \sqrt{34}}{34} \)
頂点\(D\)から面\(ACH\)に下ろした垂線を\(DI\)として図示する。
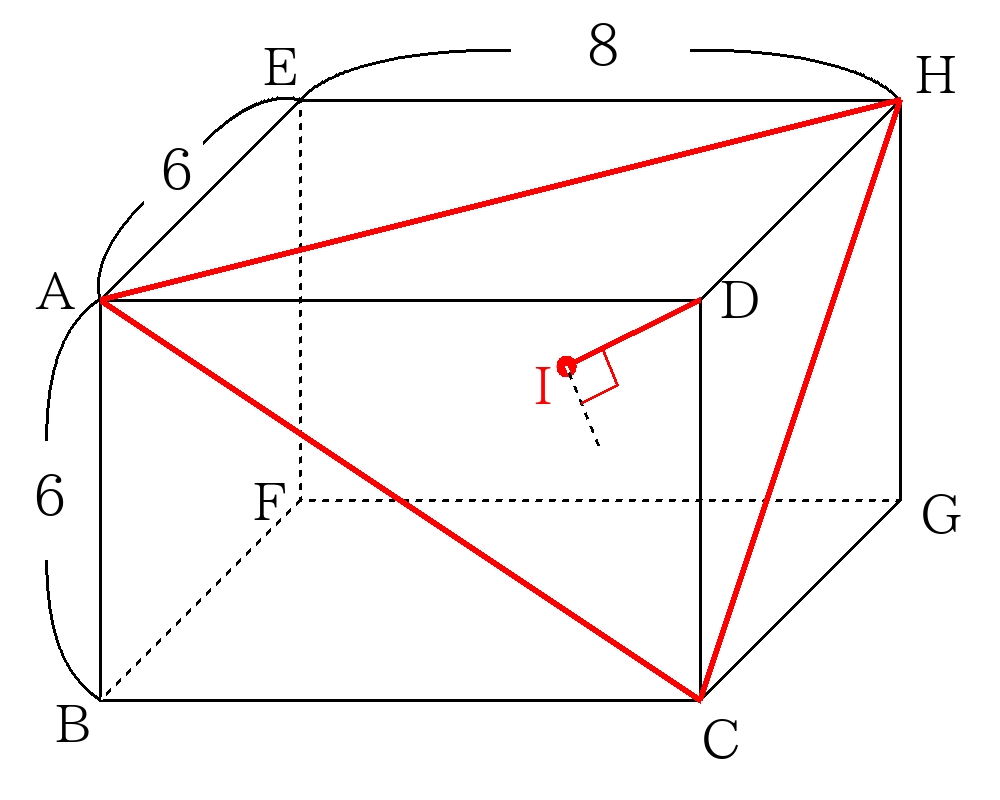
垂線\(DI\)は三角錐\(D-ACH\)の体積より逆算すれば良い。
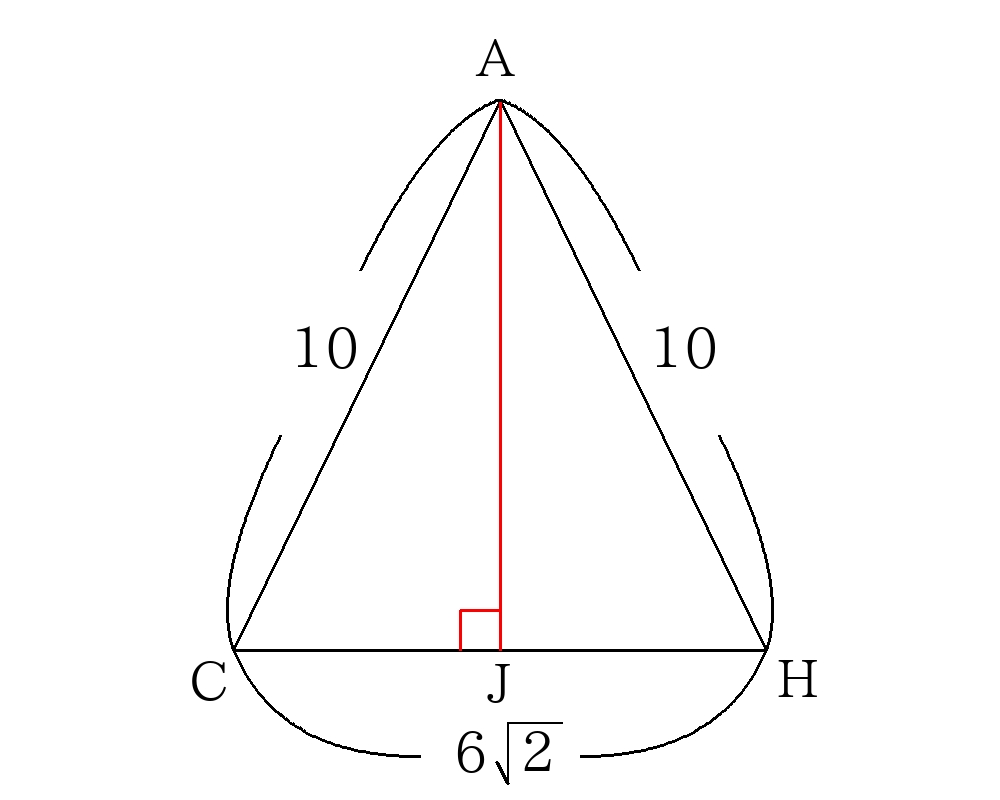
まず、\( \triangle ACH \)を求める。\(A\)から\(CH\)に下ろした垂線を\(AJ\)とすると、
\(AJ= \sqrt{10^2-(3 \sqrt{2})^2}= \sqrt{82} \)
\( \triangle ACH=6 \sqrt{2} \times \sqrt{82} \times \dfrac{1}{2}=6 \sqrt{41} \)
三角錐\(D-ACH\)の体積より
\(6 \sqrt{41} \times DI \times \dfrac{1}{3}=6 \times 6 \times 8 \times \dfrac{1}{3} \)
\(DI= \dfrac{48 \sqrt{41}}{41} \)



コメント