作図の基本
次の図のような1辺の長さが\(6\)の立方体がある。これについて次の問に答えなさい。
なお、\(AD\)の中点を\(I\)、\(DC\)の中点を\(J\)、\(EF\)の中点を\(K\)とする。
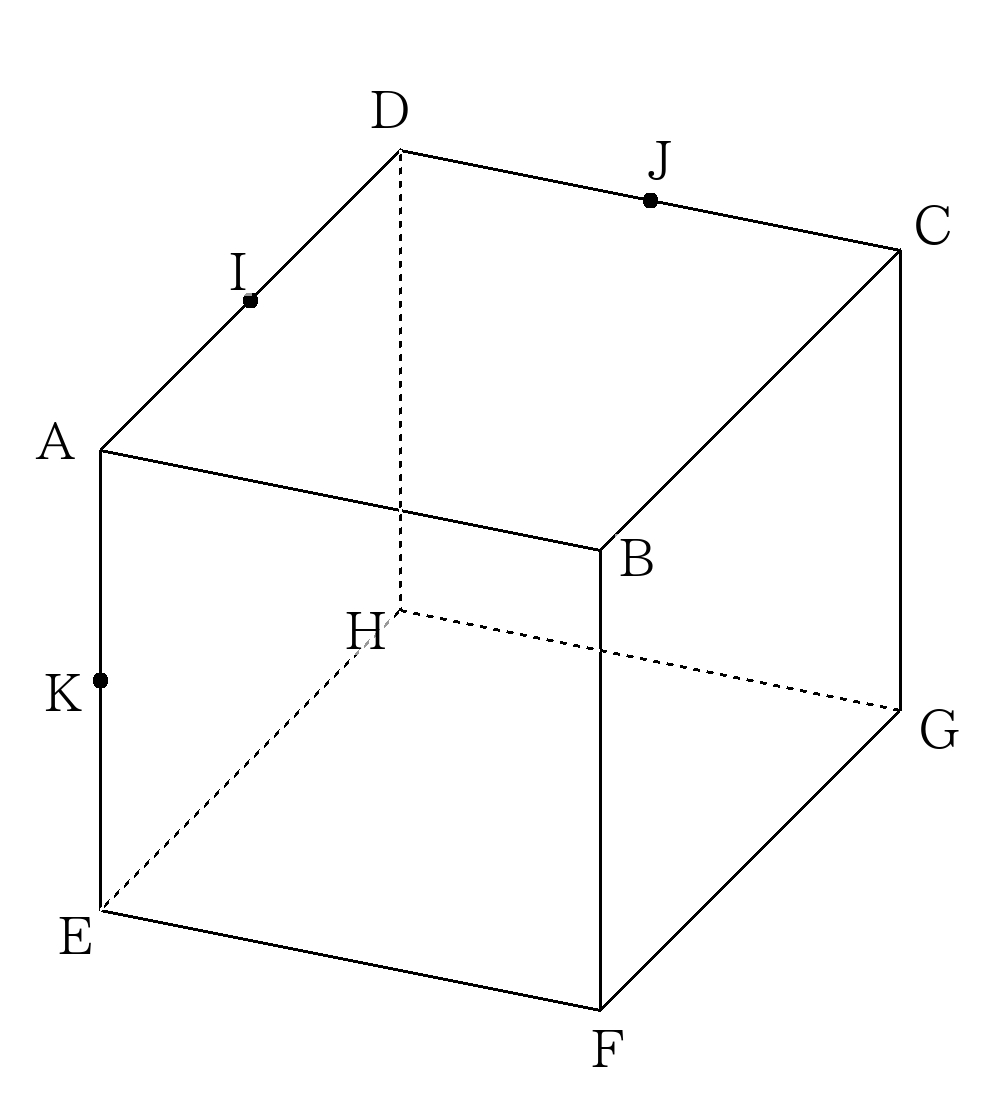
- 点\(A,C,F\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(A,D,G\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(I,J,H\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(I,J,G\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(D,F,K\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(I,J,K\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(I,J,G\)を通る平面で切断したとき、点Hを含む立体の体積を求めなさい。
- 点\(I,J,H\)を通る平面で切断したとき、点Dから切断面に垂直におろした線と切断面との交点を\(P\)とする。\(DP\)の長さを求めなさい。
作図の手順
- 同一平面上の2点を直線で結ぶ。
- 平行な面は1点を通る平行な線を引く。
- 1,2が無理なときは3つの直線を伸ばして、部屋のすみに移動させる。
例) 点\(I,J,F\)を結ぶ場合
①同一平面上の2点を直線で結ぶ。
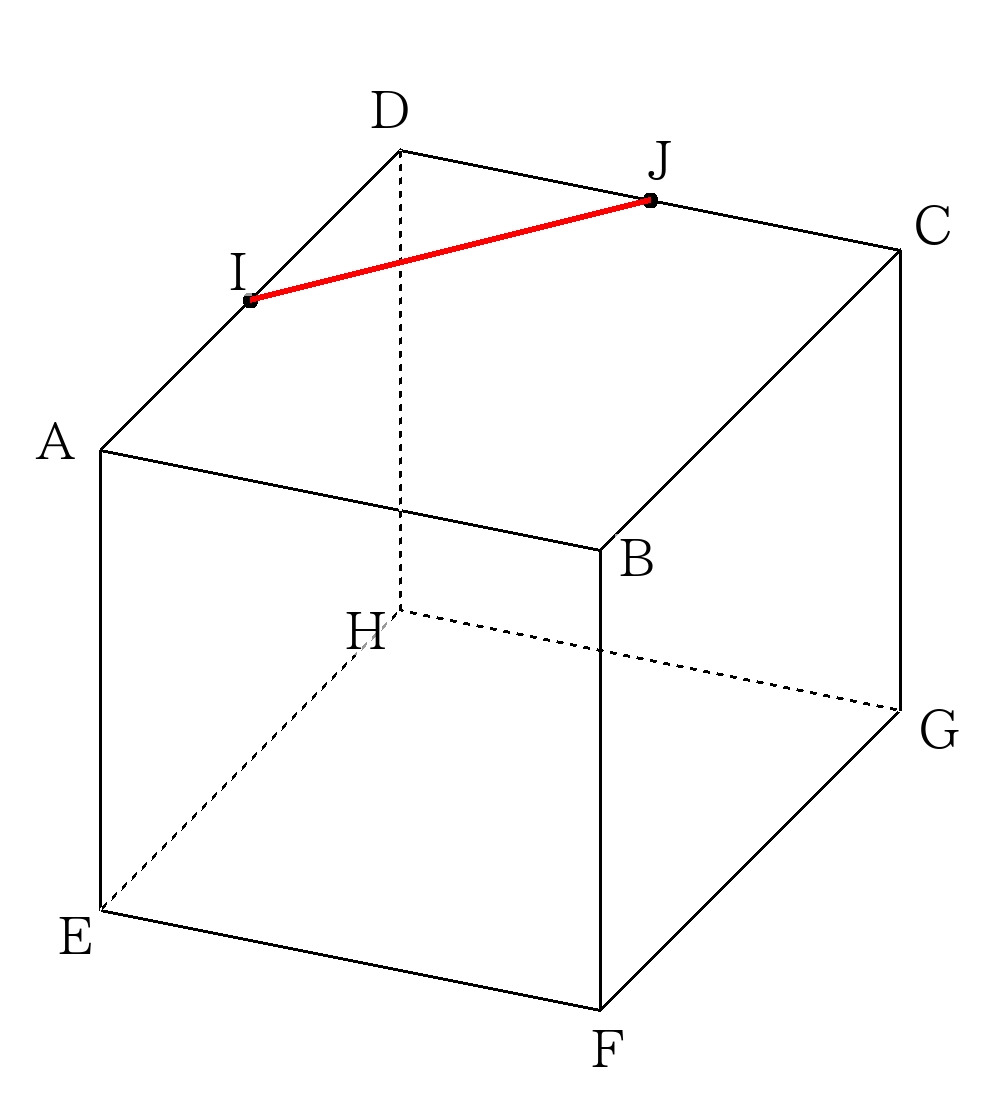
②上面の\(IJ\)に対して、点\(F\)は下面(向かい合わせの面)にあるので、点\(F\)を通り\(IJ\)に平行な線を引く。
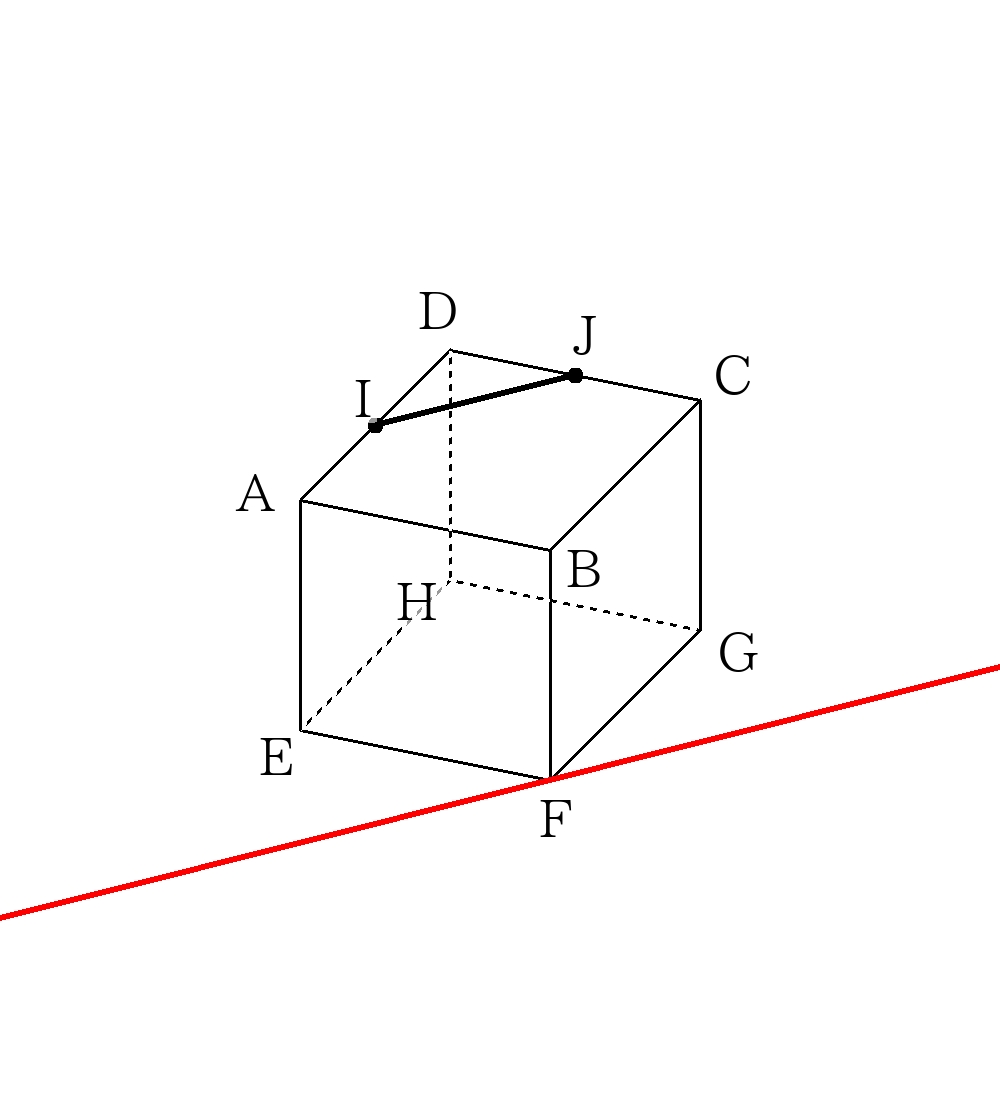
③手順が無くなったので部屋のすみに移動する。(辺を延長する。)
→Fを通る直線と左側の面(面\(AEHD\)を含む面)との交点\(P\)、\(F\)を通る直線と奥側の面(面\(DHGC\)を含む面)との交点\(Q\)ができたことを確認すること。
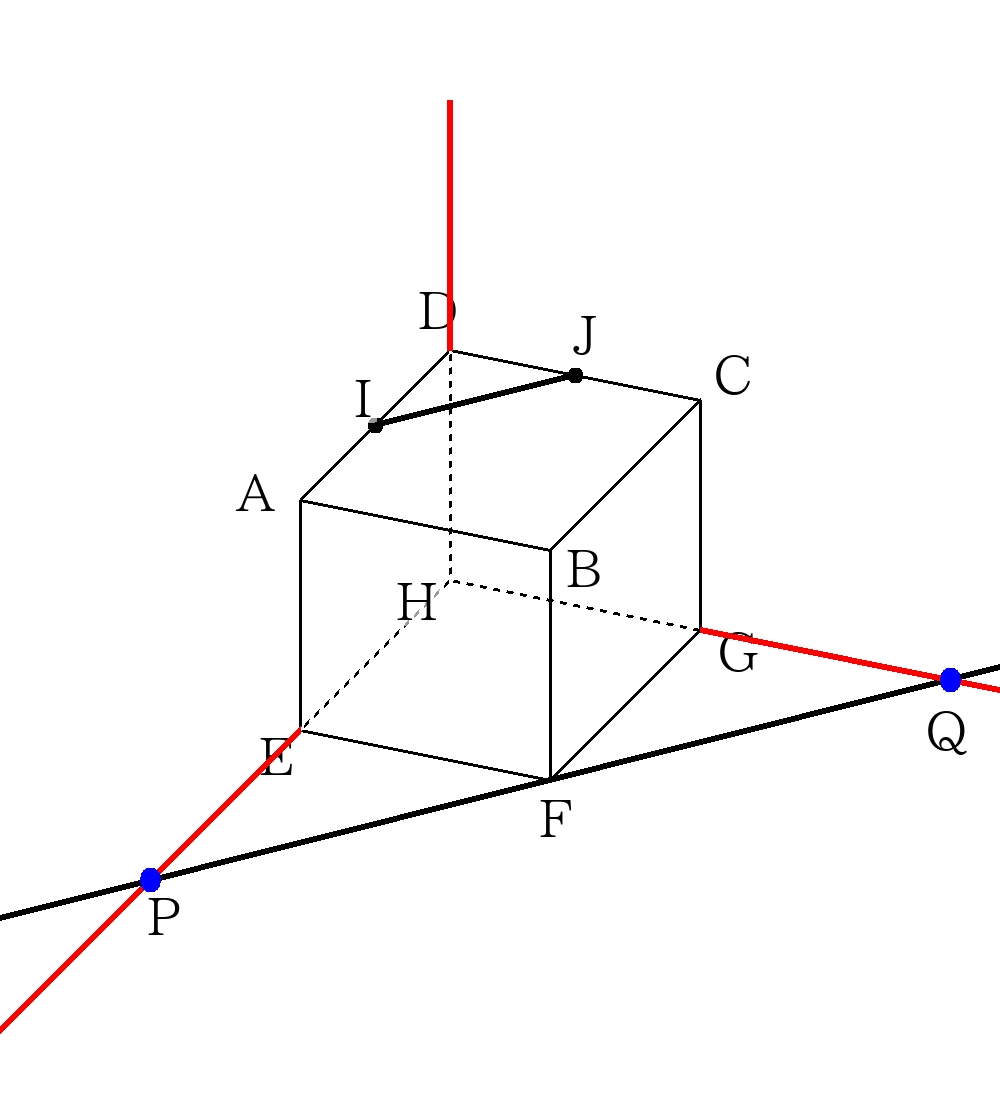
④\(PI\),\(QJ\)をそれぞれ直線で結ぶ。\(PI\)と\(AE\)の交点\(R\),\(QJ\)と\(CG\)の交点\(S\)ができたことを確認する。
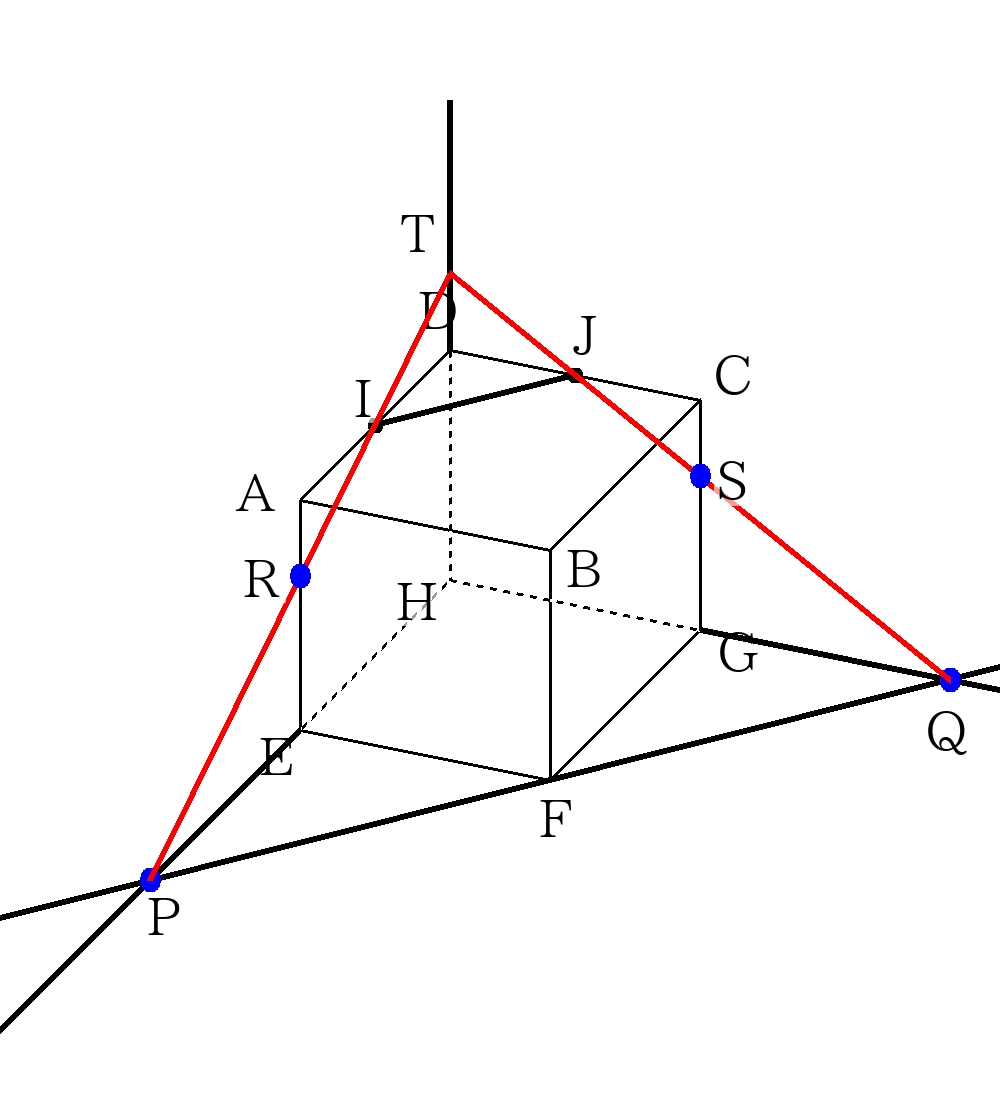
⑤\(RF\),\(SF\)をそれぞれ直線で結ぶ。
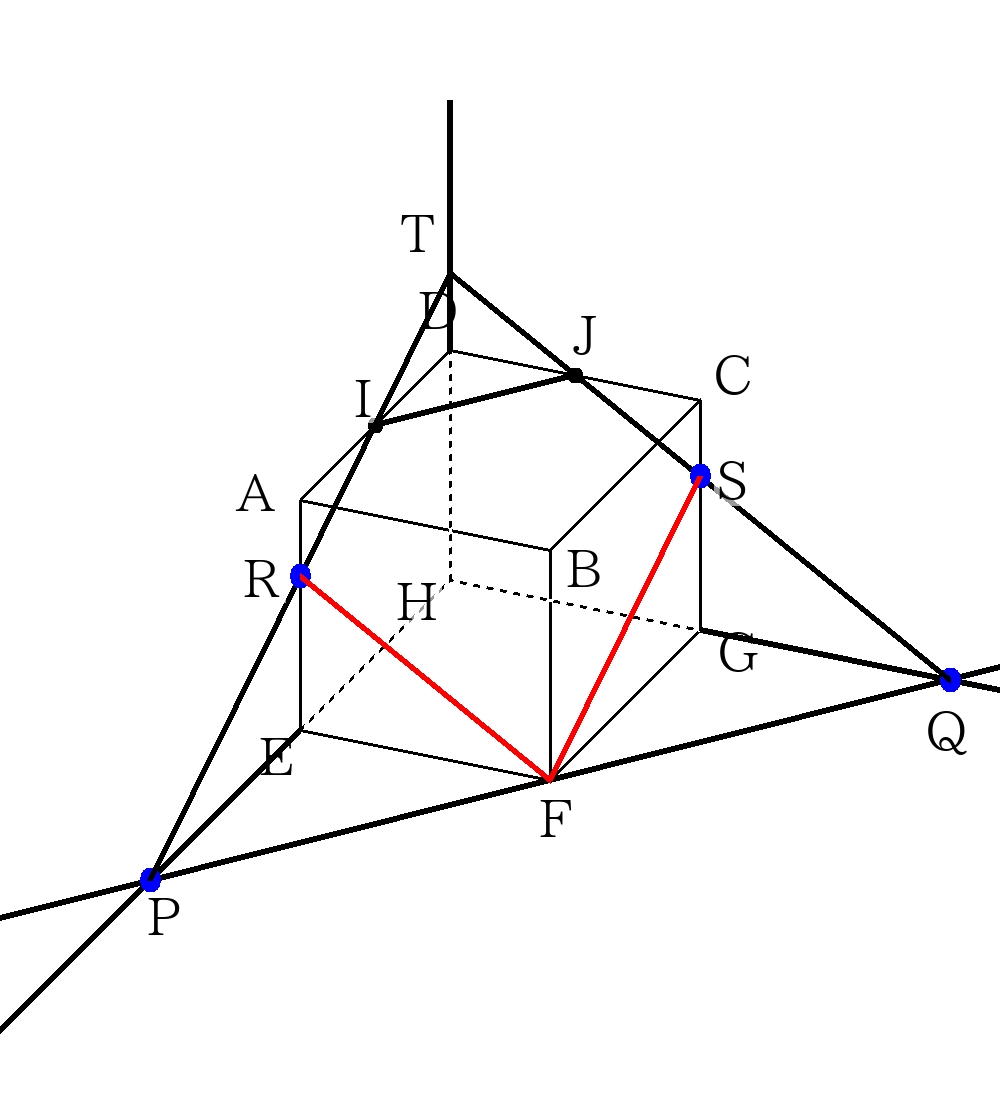
⑥完成
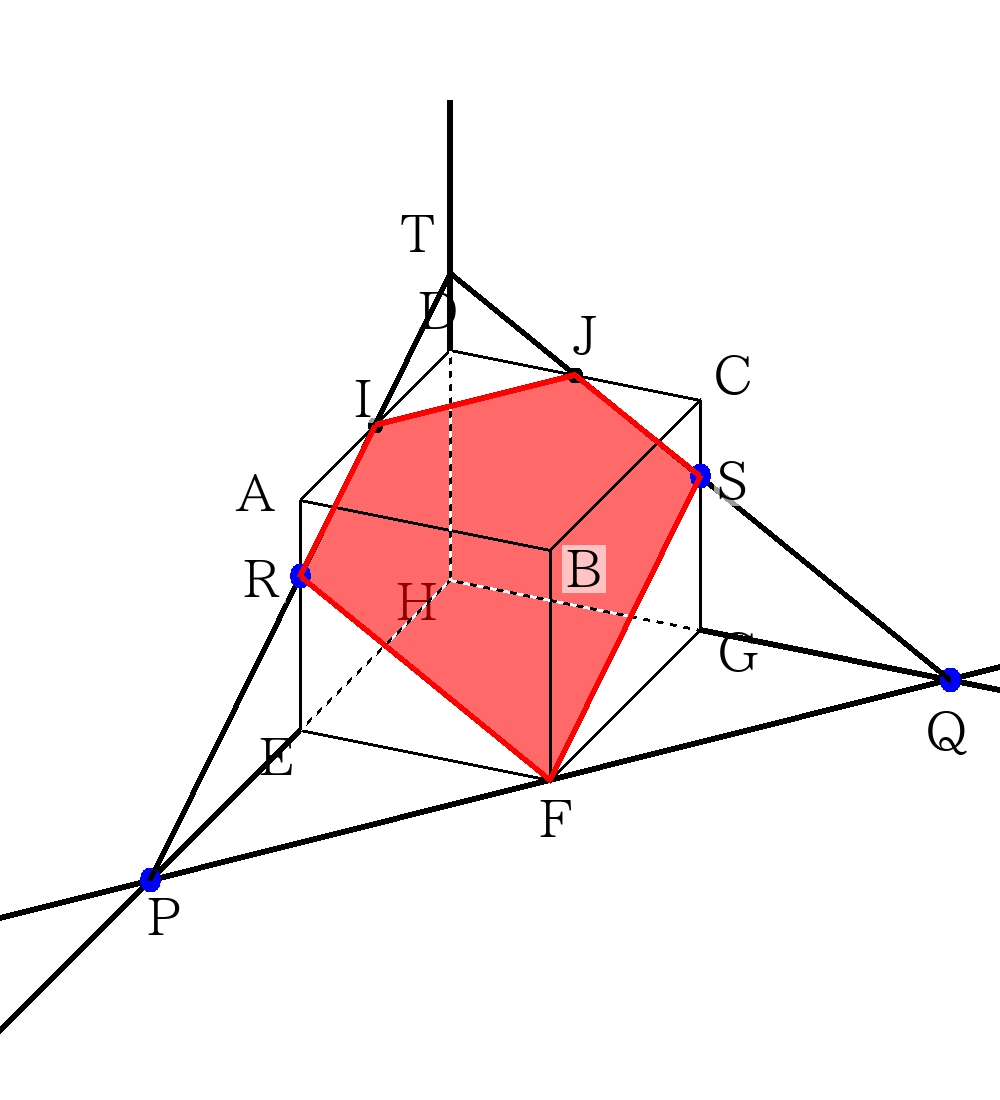
このとき\( \triangle THP \)∽\( \triangle TDI \)∽\( \triangle RAI \)∽\( \triangle REP \)等の相似を意識すること。
- 点\(A,C,F\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(A,D,G\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(I,J,H\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(I,J,G\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(D,F,K\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(I,J,K\)を通る平面で切断したとき、切断面の面積を求めなさい。
- 点\(I,J,G\)を通る平面で切断したとき、点Hを含む立体の体積を求めなさい。
- 点\(I,J,H\)を通る平面で切断したとき、点Dから切断面に垂直におろした線と切断面との交点を\(P\)とする。\(DP\)の長さを求めなさい。
作図すると
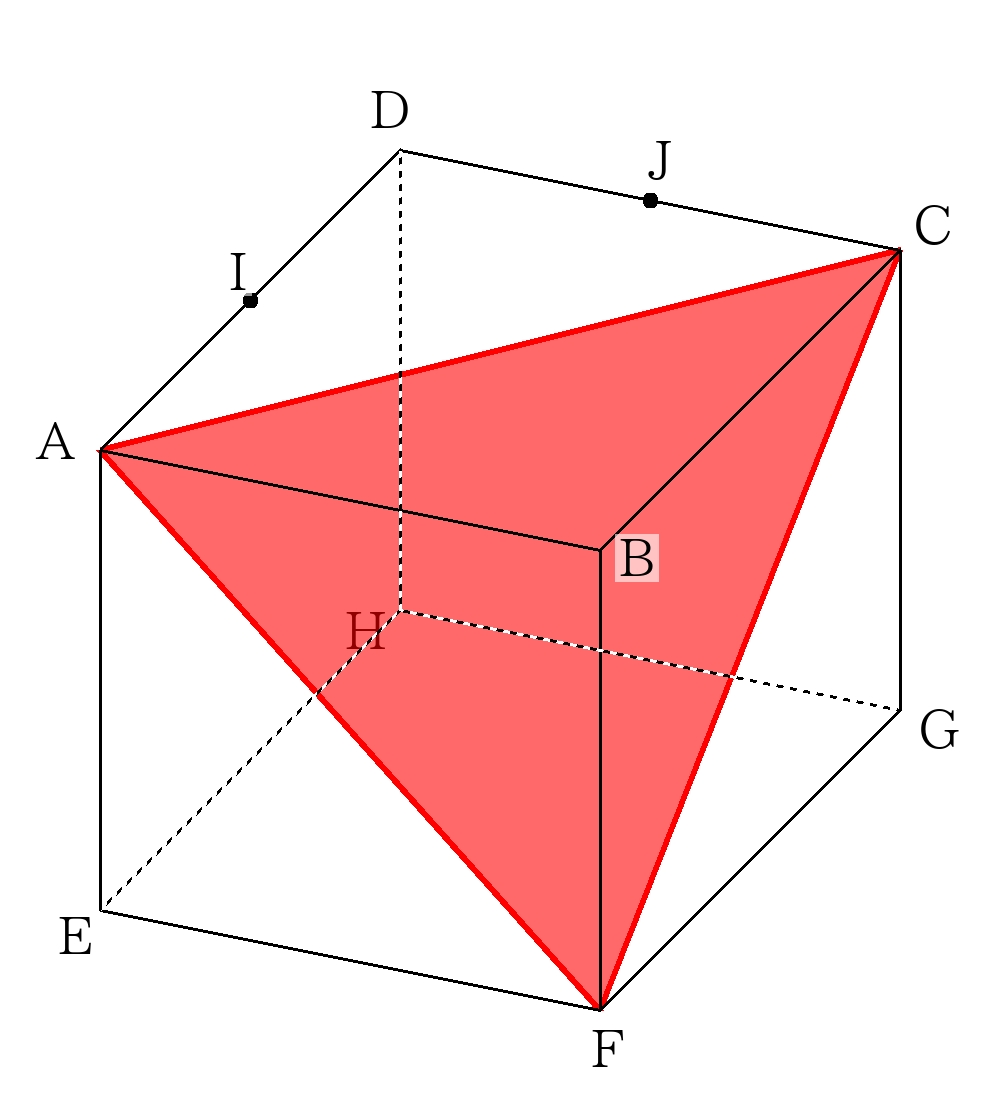
切断面\( \triangle ACF\)は1辺\(6 \sqrt{2} \)の正三角形なので、
\( \dfrac{ \sqrt{3}}{4} \times \left(6 \sqrt{2} \right)^{2}=18 \sqrt{3} \)
\(18 \sqrt{3} \)
※1辺の長さが\(a\)の正三角形の高さ\( h=\dfrac{\sqrt{3}}{2}a \)、面積\(S=\dfrac{\sqrt{3}}{4}a^{2}\)は必ず覚えておくこと。
作図すると
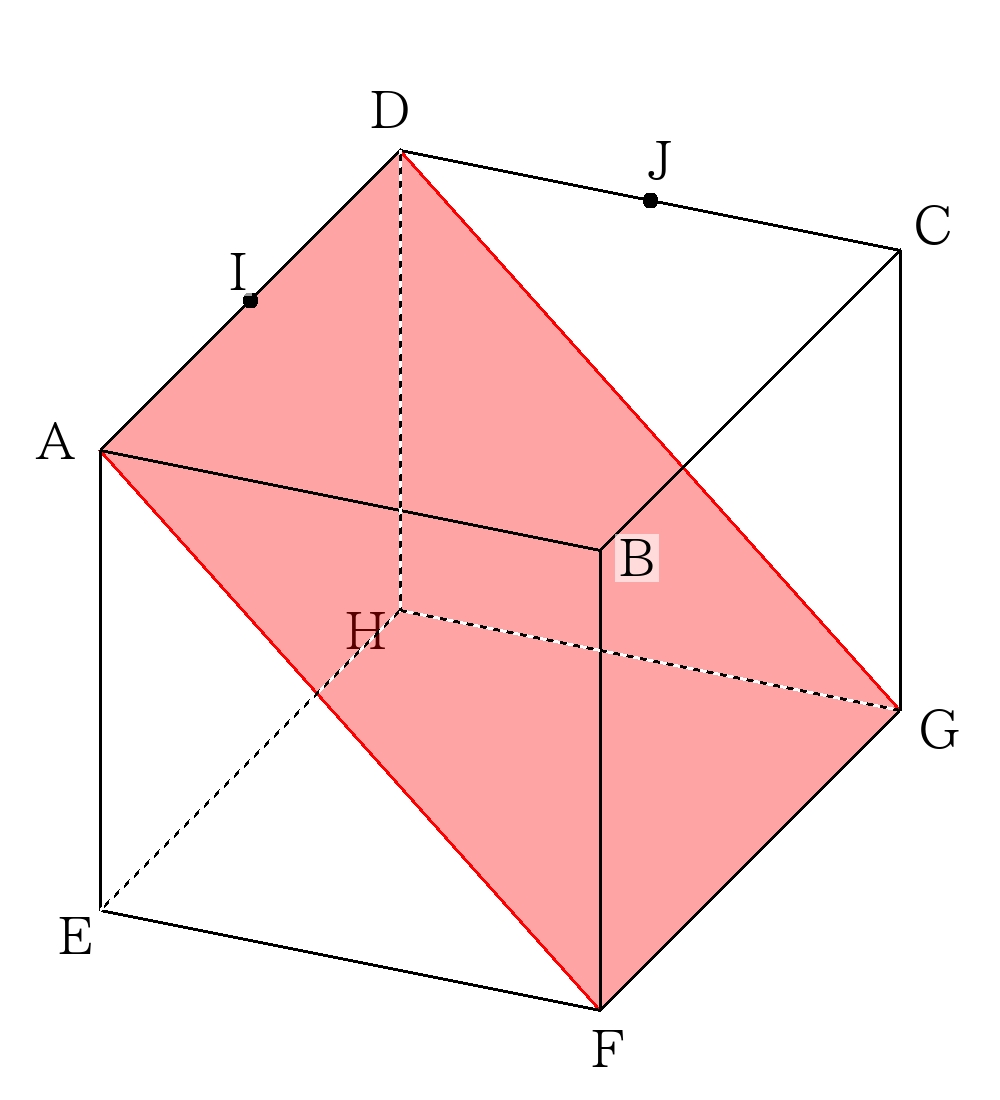
切断面 \(\Box AFGD\)の面積は、\(6 \times 6\sqrt{2}=36 \sqrt{2}\)
\(36 \sqrt{2} \)
作図すると
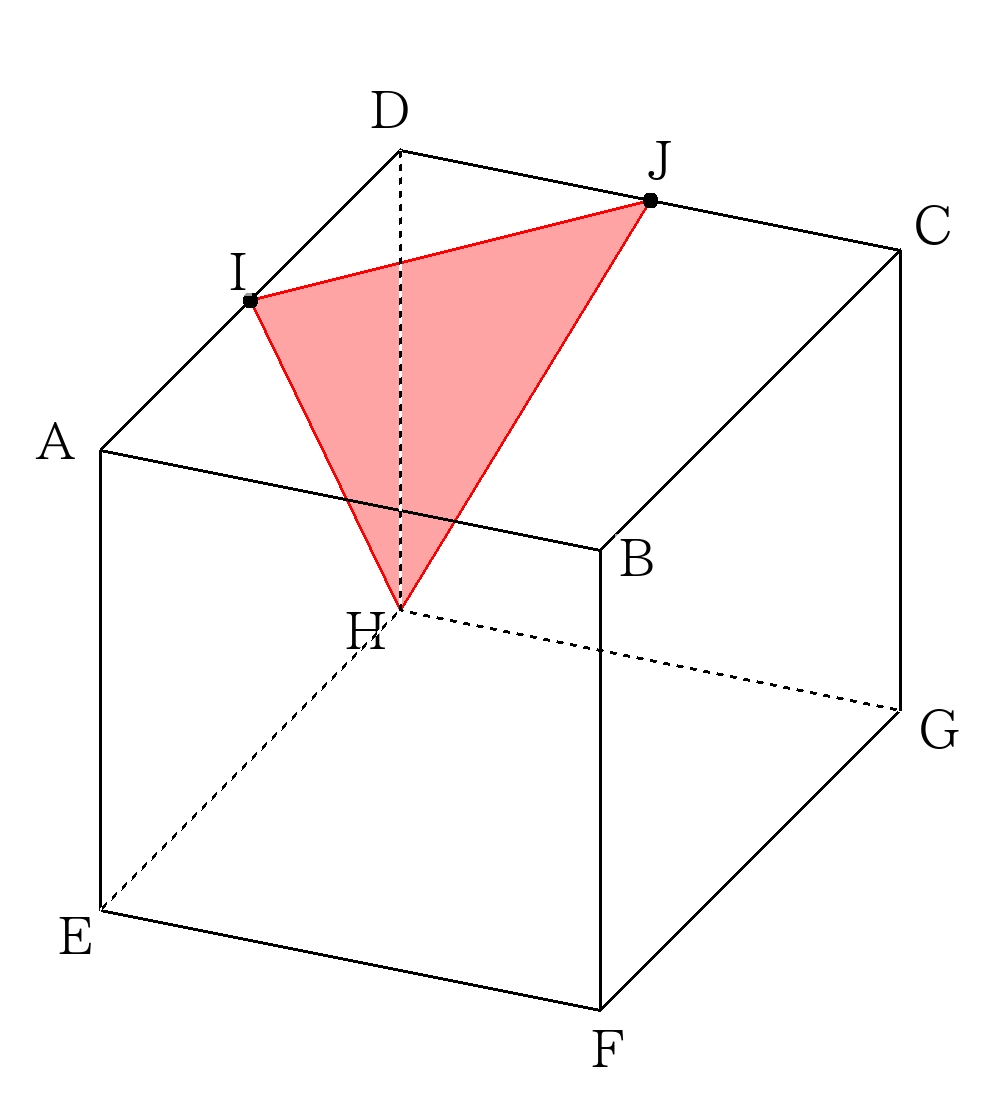
切断面は\( \triangle HIJ \)は\(HI=IJ\)の二等辺三角形で、\(IJ=3\sqrt{2}、HI=IJ=3\sqrt{5}\)
\(h^2= \left(3 \sqrt{5} \right)^{2}- \left( \dfrac{3 \sqrt{2}}{2} \right)^2 \)
\(h= \dfrac{9 \sqrt{2}}{2} \)
よって面積は
\(3 \sqrt{2} \times \dfrac{9 \sqrt{2}}{2} \times \dfrac{1}{2}= \dfrac{27}{2} \)
\( \dfrac{27}{2} \)
作図すると
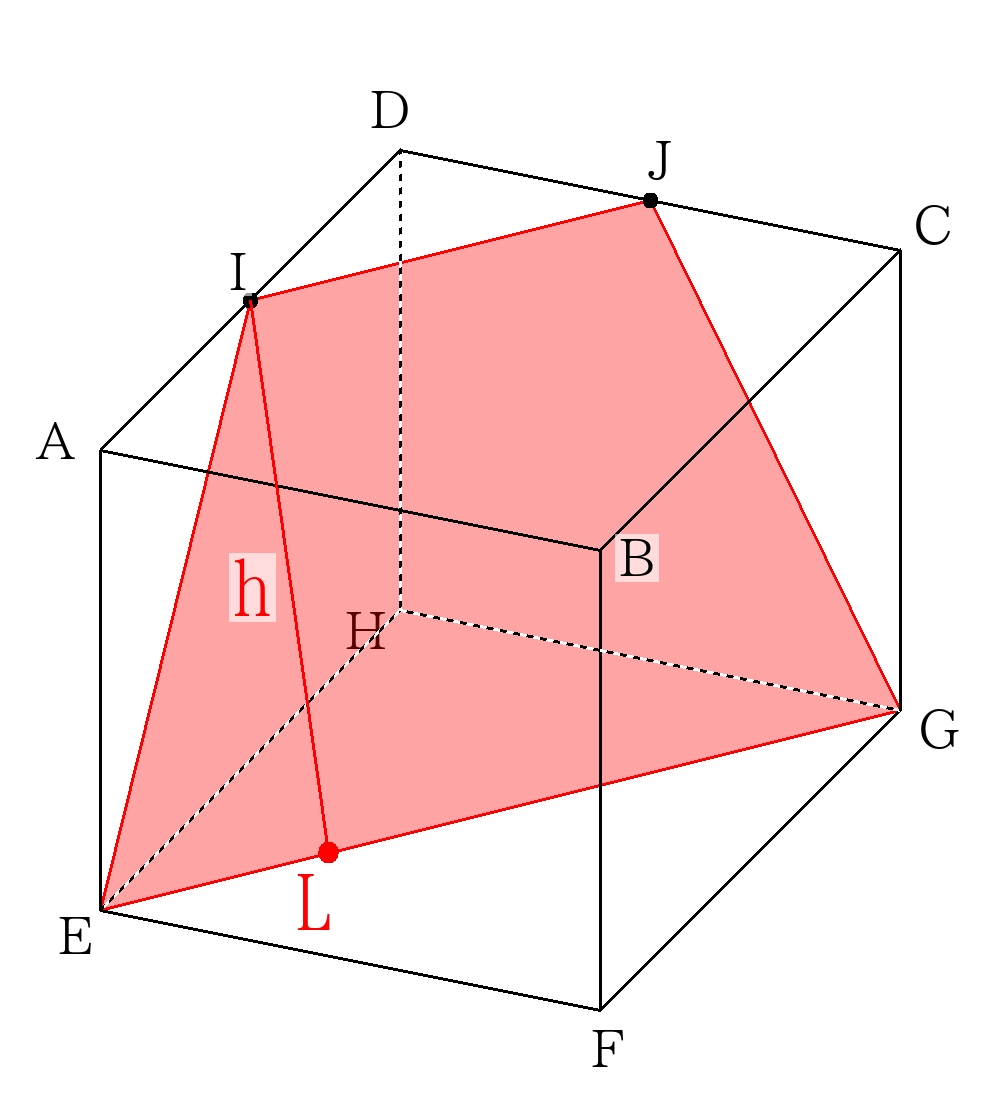
切断面の四角形\(IEGJ\)は\(IJ=3\sqrt{2},EG=6\sqrt{2},IE=JG=3\sqrt{5}\)の等脚台形
\(EL= \dfrac{1}{2}(6 \sqrt{2}-3 \sqrt{2})= \dfrac{3 \sqrt{2}}{2} \)
\(h^2= \left(3 \sqrt{5} \right)^{2}- \left( \dfrac{3 \sqrt{2}}{2} \right)^2 \)
\(h= \dfrac{9 \sqrt{2}}{2} \)
よって台形\(IEGJ\)の面積は、
\((3 \sqrt{2}+6 \sqrt{2}) \times \dfrac{9 \sqrt{2}}{2} \times \dfrac{1}{2}= \dfrac{81}{2} \)
\( \dfrac{81}{2} \)
作図すると
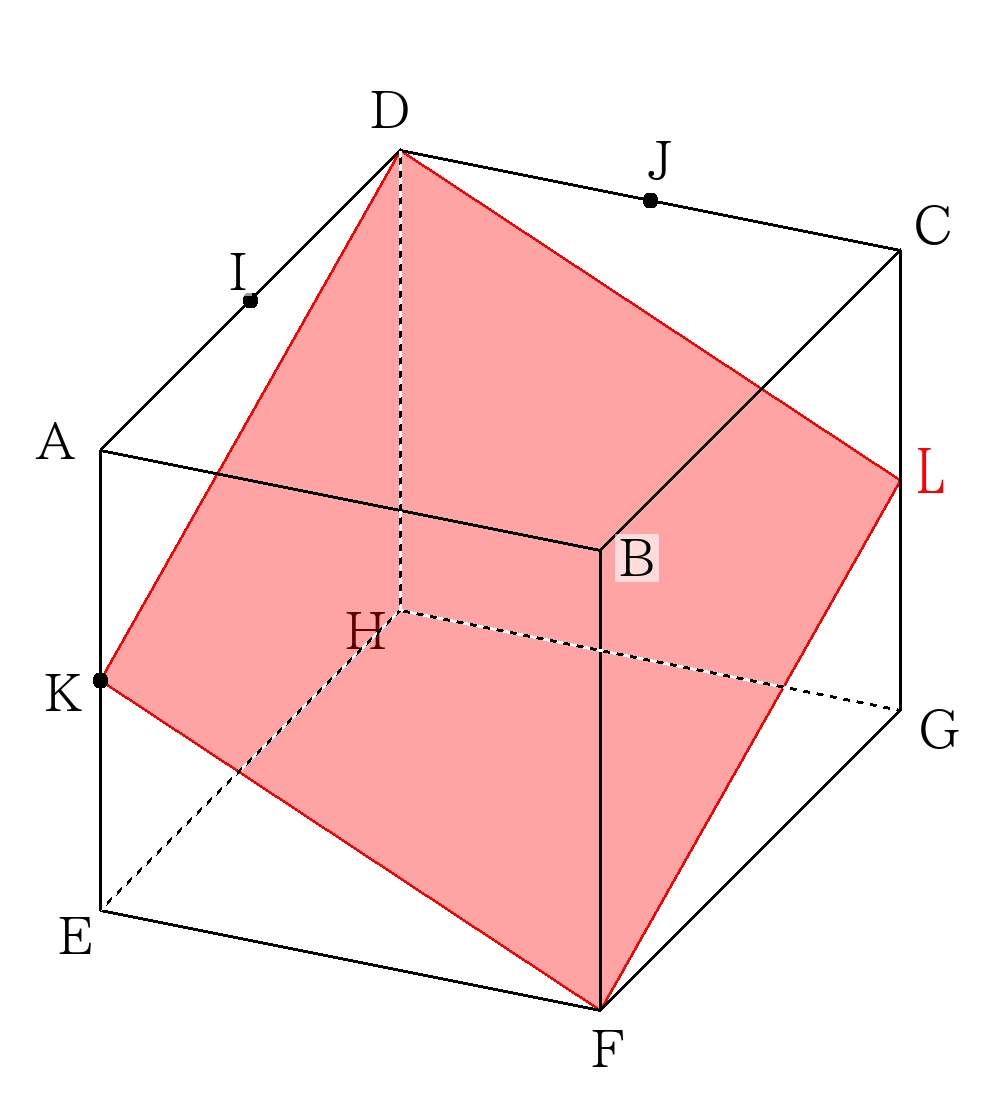
切断面の四角形\(DKFJ\)はひし形であり、ひし形の面積は(対角線)×(対角線)÷2で計算できる。
\(6 \sqrt{3} \times 6 \sqrt{2} \div2=18 \sqrt{6},false \)
\(18 \sqrt{6} \)
作図すると
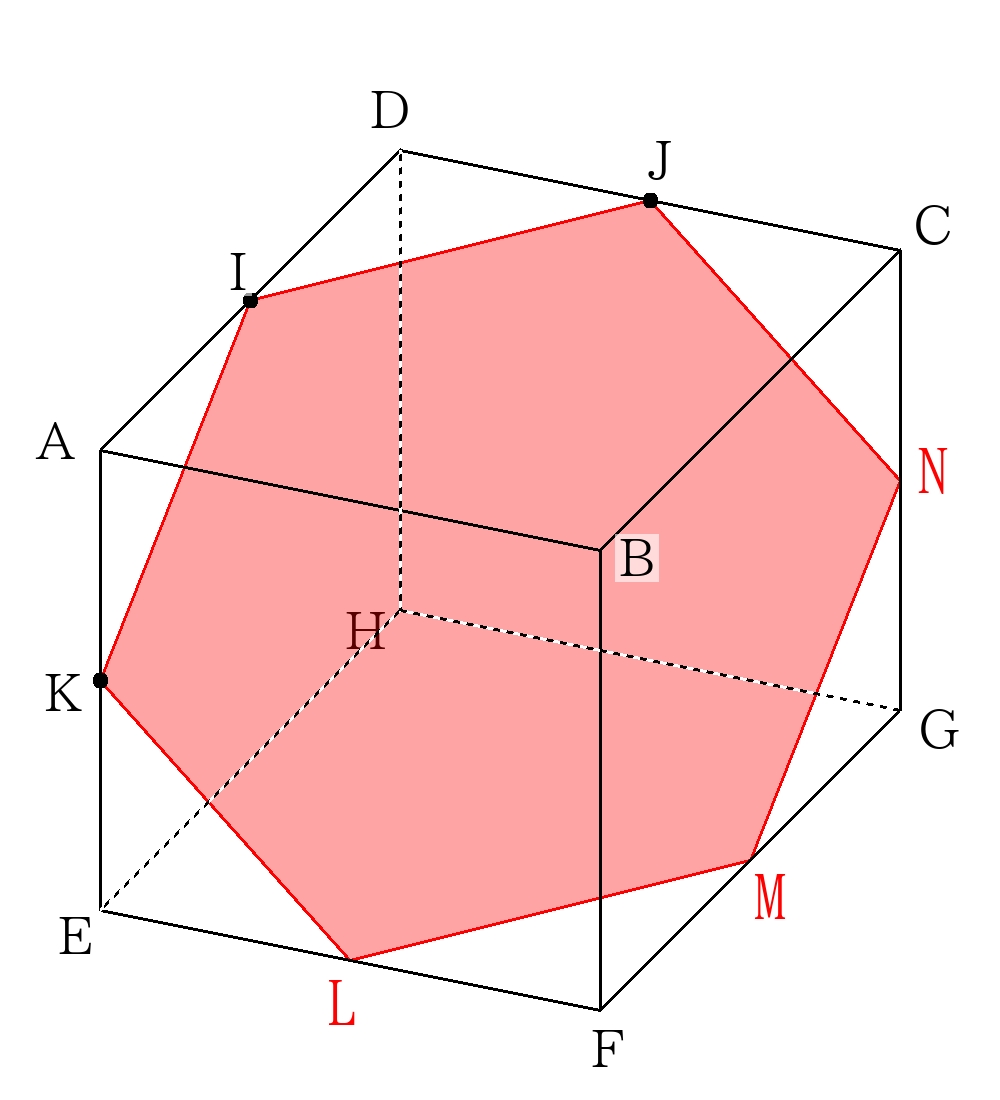
切断面は六角形\(IKLMNJ\)になる。六角形は正三角形が6つ集まった図形なのでその面積は、
\( \dfrac{ \sqrt{3}}{4} \times \left(3 \sqrt{2} \right)^2 \times 6=27 \sqrt{3} \)
\(27 \sqrt{3} \)
作図すると
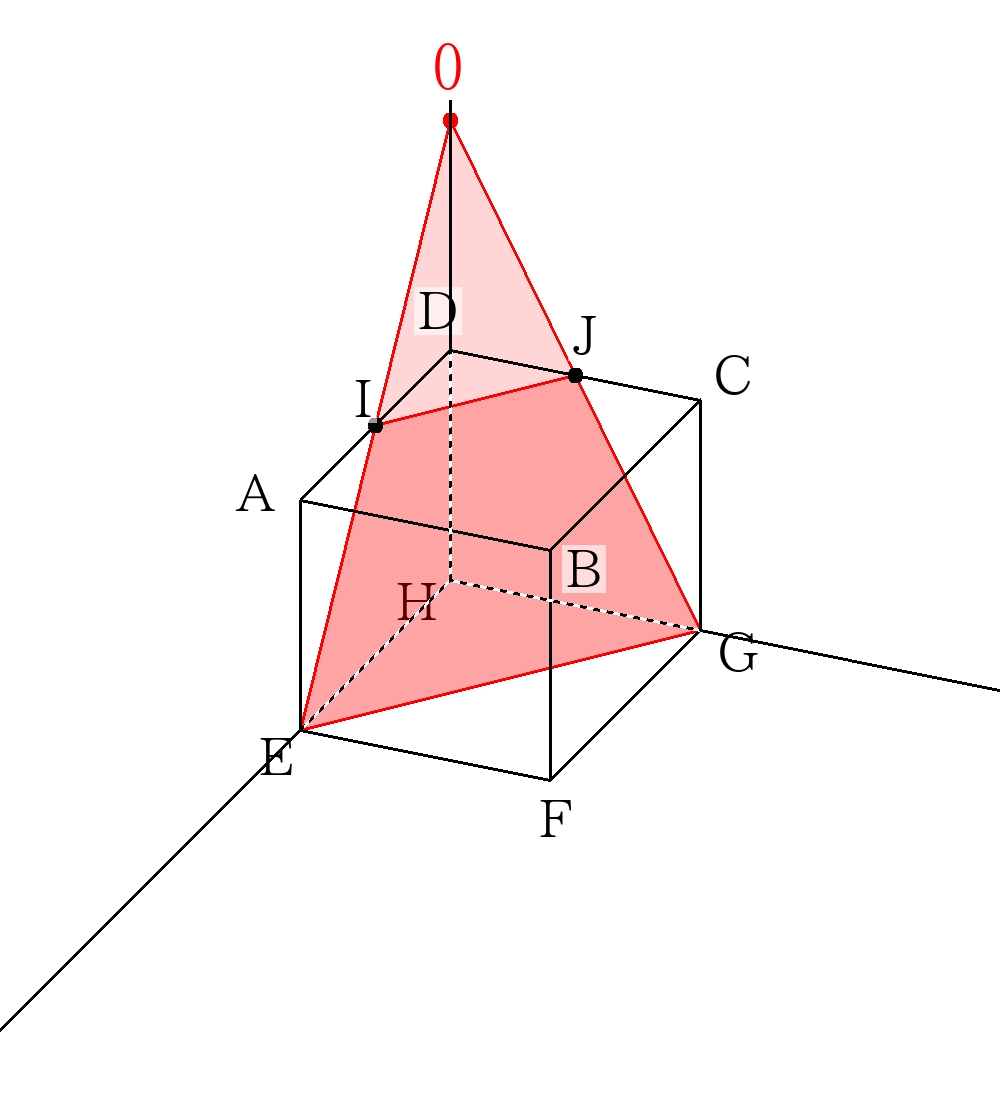
求める体積は三角錐\(O-HEG\)から三角錐\(O-DIJ\)を引いた体積。
\(6 \times 6 \times \dfrac{1}{2} \times 12 \times \dfrac{1}{3} \times \dfrac{8-1}{8}=63 \)
\(63 \)
作図すると

DPは、三角錐\(D-IJH\)の面\(IJH\)を底面にしたときの高さである。
③より、\(IJH\)の面積は\(\dfrac{27}{2}\)
体積と底面積から高さ(\(DP\))を計算する。
\( \dfrac{27}{2} \times DP \times \dfrac{1}{3}=9 \)
\(DP=2,false \)
\(DP=2 \)



コメント