正方形の折り返し
次の図のような1辺\(18\)の正方形\(ABCD\)があり、線分\(EF\)を折り目として折り曲げたところ、頂点\(A\)は頂点\(A’\)、頂点\(B\)は頂点\(B’\)に移った。
\(AE=10\)のとき、次の問に答えなさい。なお、点\(G\)は\(A’B’\)と\(BC\)との交点である。
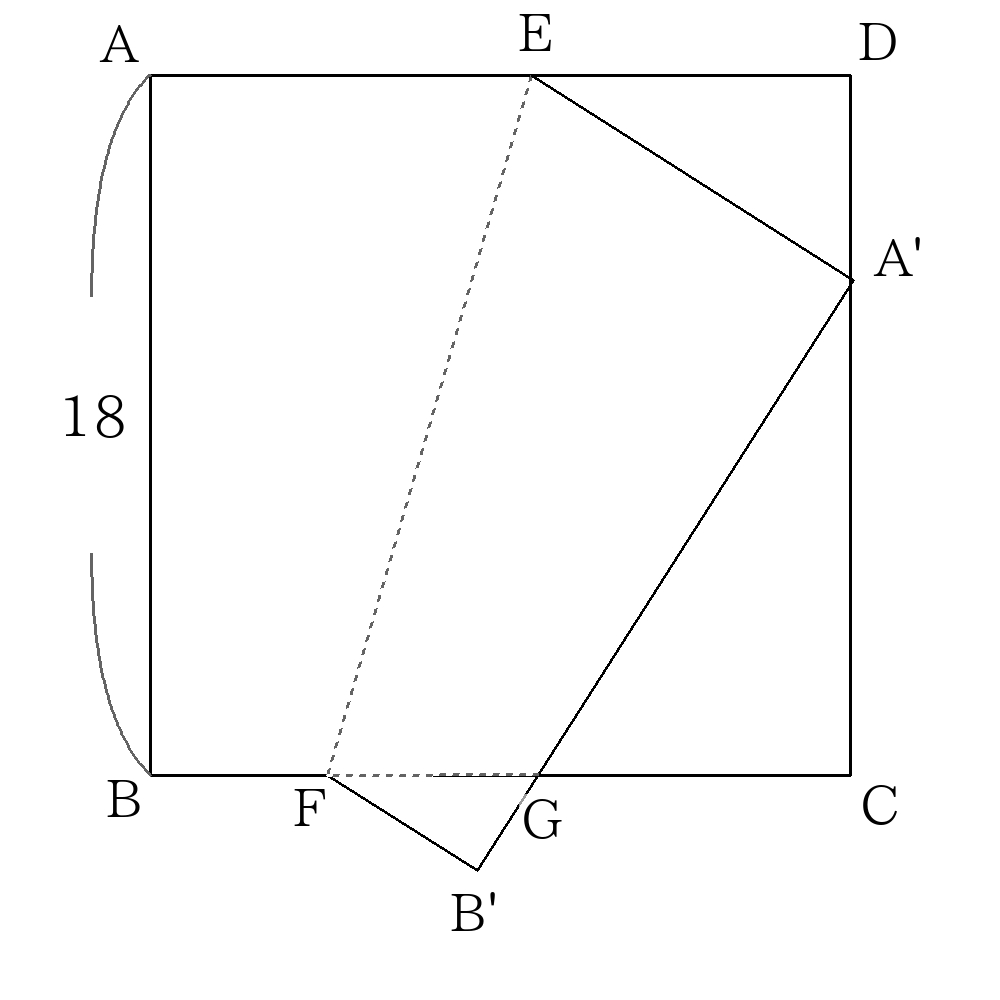
- \(B’F\)の長さを求めなさい。
- 四角形\(A’EFG\)の面積を求めなさい。
- \(EF\)の長さを求めなさい。
- 直角三角形に印を書き入れる。(〇+☓=90度)
- 相似と三平方で計算する。
相似な三角形を見つけたら計算するだけ。
外接円の半径の求め方
- \(B’F\)の長さを求めなさい。
- 四角形\(A’EFG\)の面積を求めなさい。
- \(EF\)の長さを求めなさい。
直角三角形に記号を書き入れる。
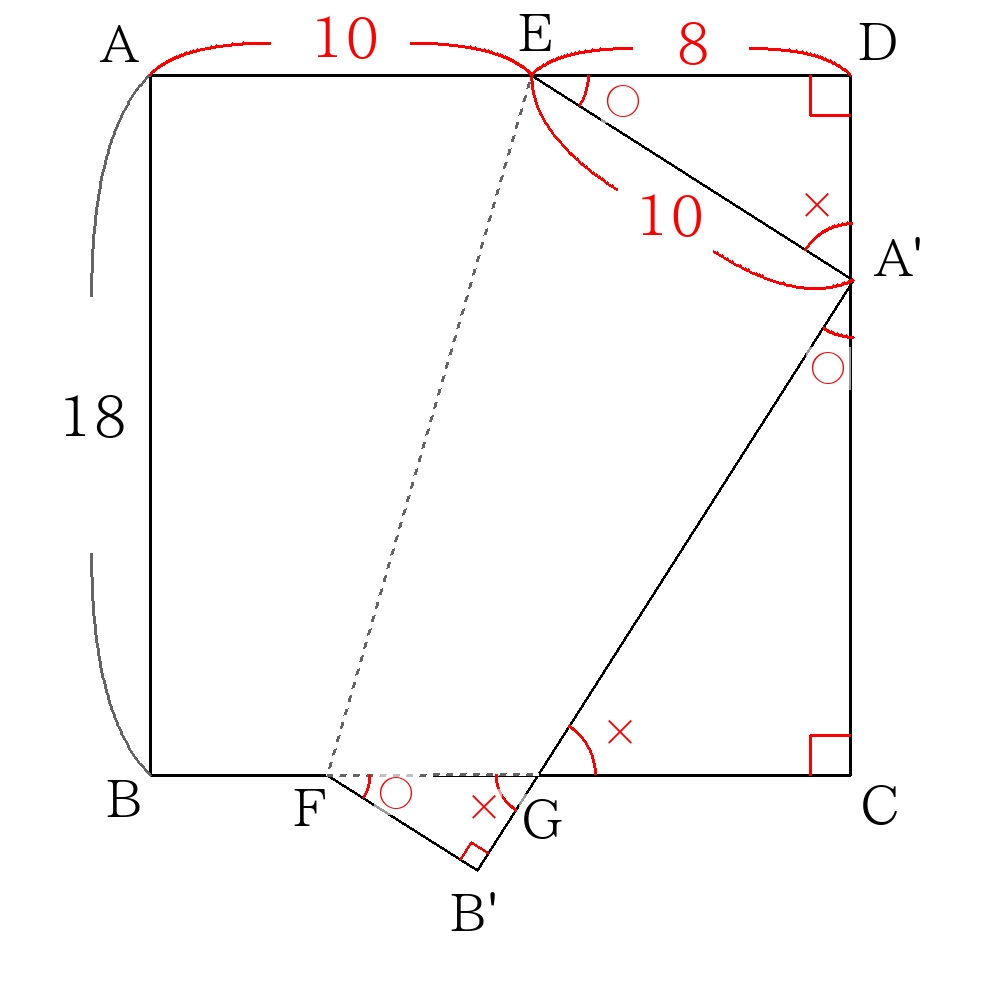
(ここで、\(\triangle A’DE\)∽\(\triangle GCA’\)∽\(\triangle GB’F\)であることに注目しておくこと。)
\(\triangle DEA’\)において三平方の定理より
\(A’D= \sqrt{10^2-8^2}=6 \)
\(A’C=18-6=12 \)
\(\triangle GCA’\)∽\(\triangle A’DE\)であり、\(GC:CA’:A’G=A’D:DE:EA’=3:4:5\)の辺の比なので
\(GC=12 \times \dfrac{3}{4}=9 \)
\(A’G=12 \times \dfrac{5}{4}=15 \)
また、
\(GB’=18-15=3 \)
さらに、\(\triangle GB’F\)∽\(\triangle GCA’\)であり、\(GB’:B’F:FG=GC:CA’:A’G=3:4:5\)の辺の比なので
\(B’F=3 \times \dfrac{4}{3}=3 \)
\(FG=3 \times \dfrac{5}{3}=5 \)
\(B’F=4 \)
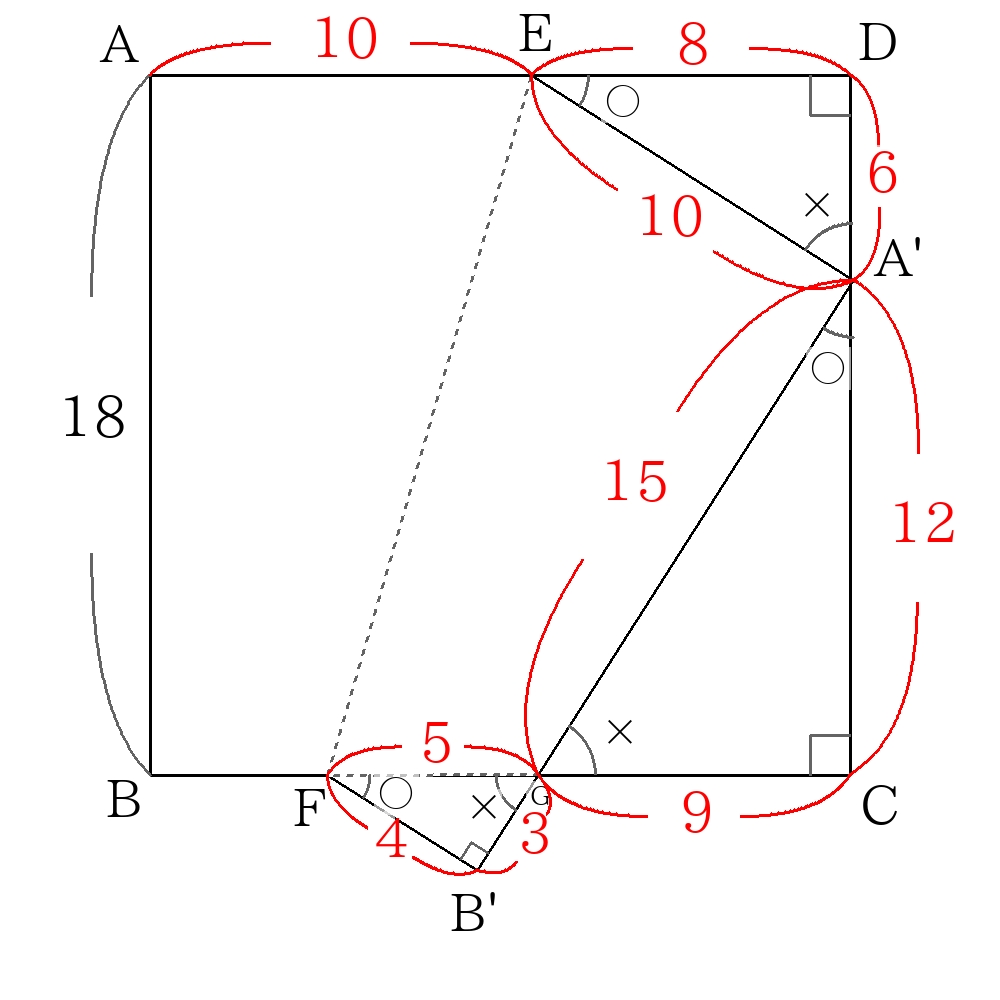
(四角形\(A’EFG\))=(台形\(A’EFB’\))-(直角三角形\(GB’F\))で求まるので
\((5+10) \times 18 \times \dfrac{1}{2}-3 \times 4 \times \dfrac{1}{2}=129 \)
\(129 \)
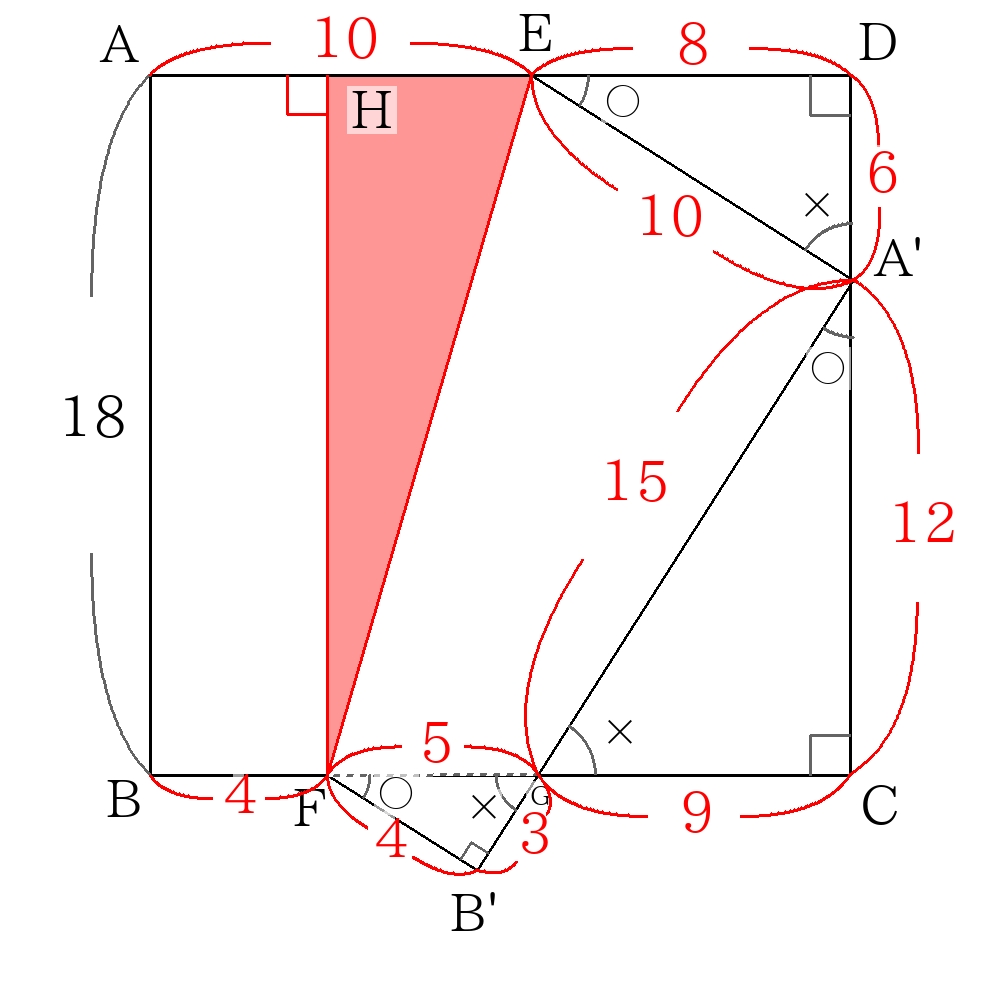
点\(F\)から\(AD\)に垂線\(FH\)を引く。
直角三角形\(FHE\)において三平方の定理より
\(FE= \sqrt{18^2+(10-4)^2}=6 \sqrt{10} \)
\(EF=6 \sqrt{10} \)



コメント