特別角の三角形
次の図の三角形\(ABC\)において、\(x\)、\(y\)の長さをそれぞれ求めなさい。
- 三角形の分割の仕方を覚えておくこと。
- (45度、60度、75度)の三角形の辺の比は3秒で書き込めるようにしておくこと。
※30度、60度の直角三角形から\(1:2:\sqrt{3}\)、そのまま45度の直角三角形に移って\(\sqrt{3}:\sqrt{3}:\sqrt{6}\)と書き込めば良い。
※(45度→60度→75度の順で)\((1+\sqrt{3}):2:\sqrt{6}\)を覚えておくのが望ましい。
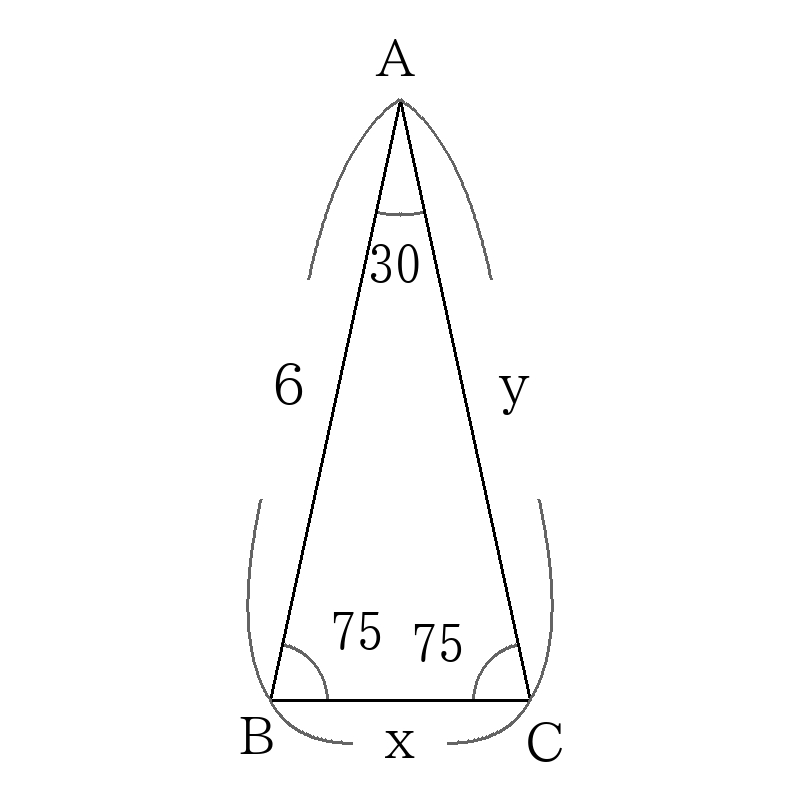
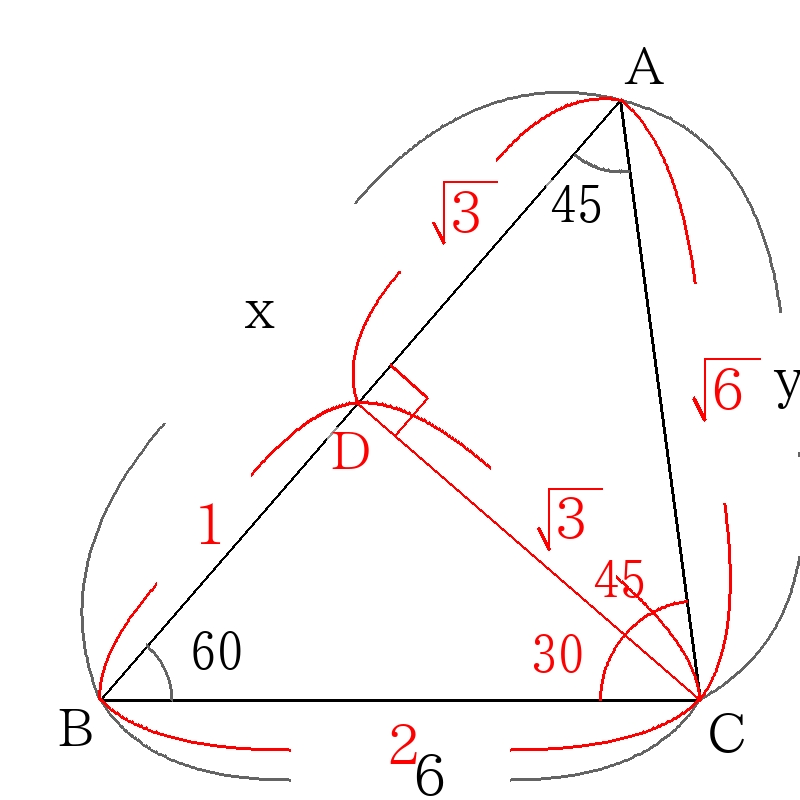
頂点\(C\)から辺\(AB\)に引いた垂線を\(CD\)とする。
30度,60度の直角三角形の辺の比、45度の直角二等辺三角形の辺の比を利用して、図のようにすべての辺の長さの比を書き込む。
比の2にあたる長さが6なので、
\(x=3 \sqrt{3}+3,y=3 \sqrt{6} \)
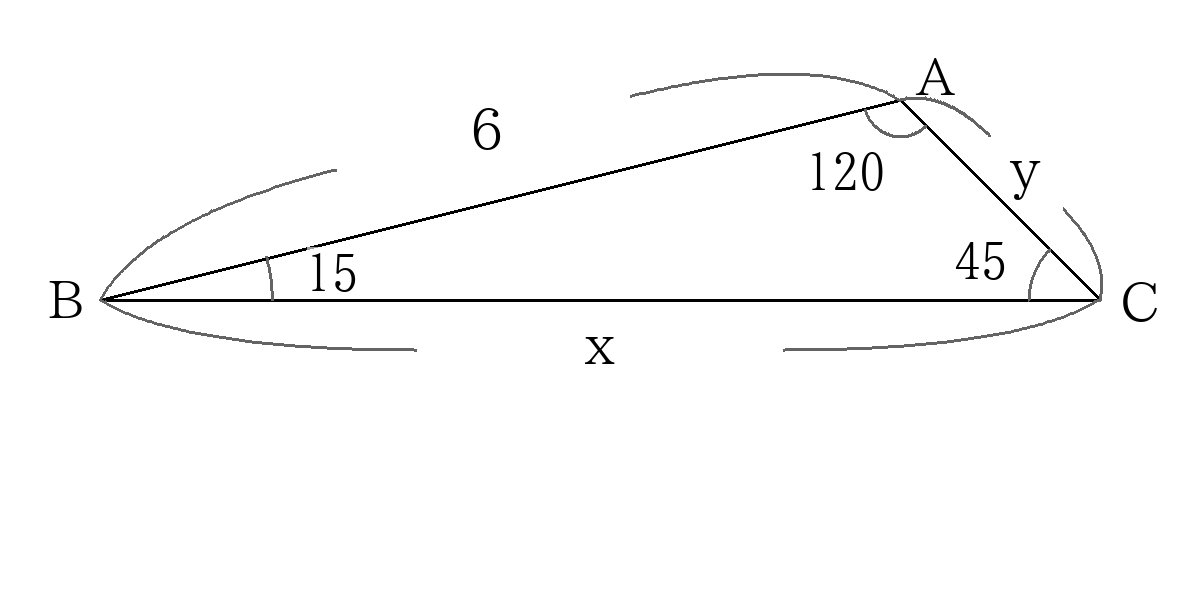
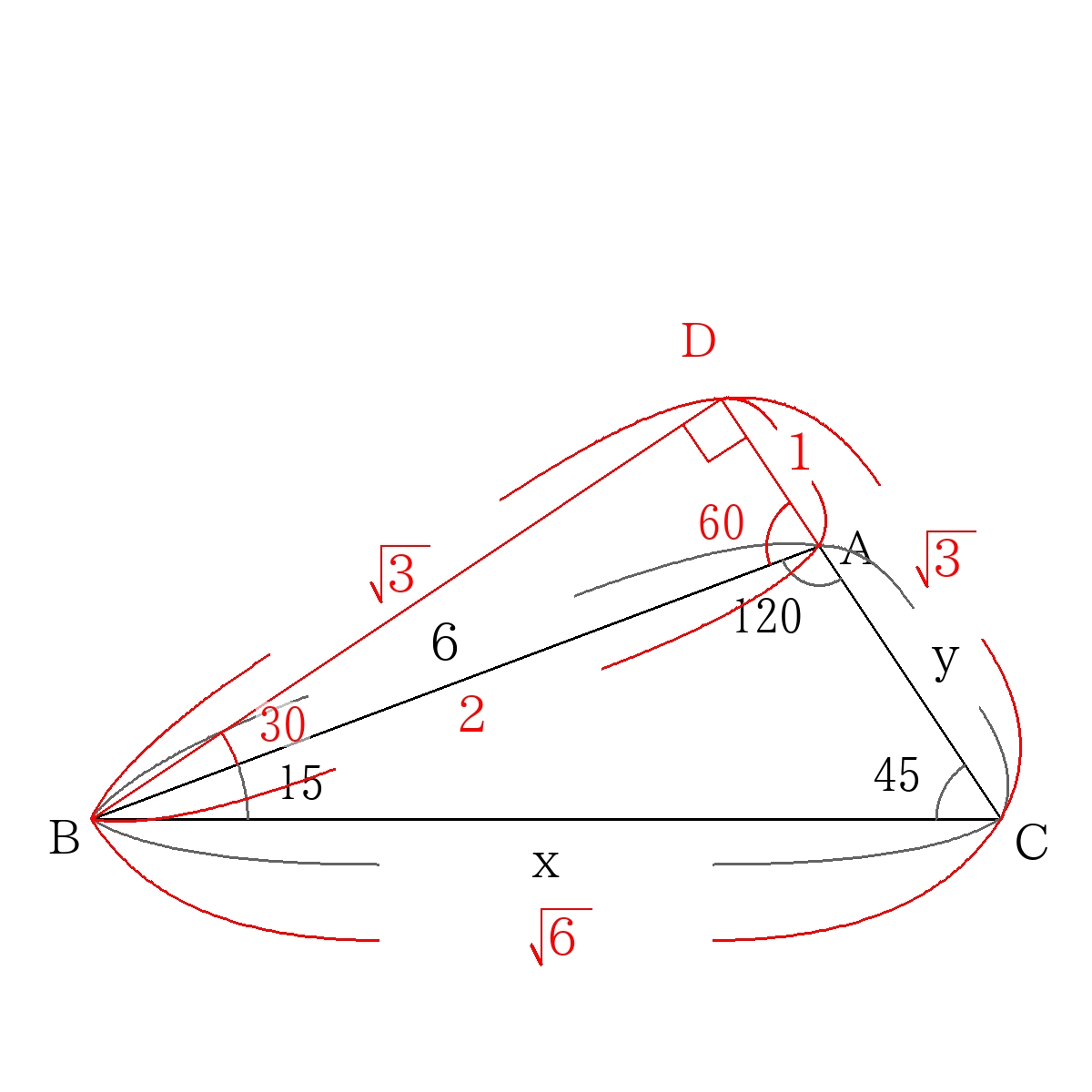
頂点\(B\)から直線\(AC\)に引いた垂線を\(BD\)とする。
すると、三角形\(BAD\)は30度、60度の直角三角形
三角形\(DBC\)は\(DB=DC\)の直角二等辺三角形三角形であるので、図のように辺の長さの比を書き入れる。
比の2にあたる長さが6なので、
\(x=3 \sqrt{6} \)
\(y=3 \left( \sqrt{3}-1 \right) \)
\(x=3 \sqrt{6},y=3 \left( \sqrt{3}-1 \right) \)
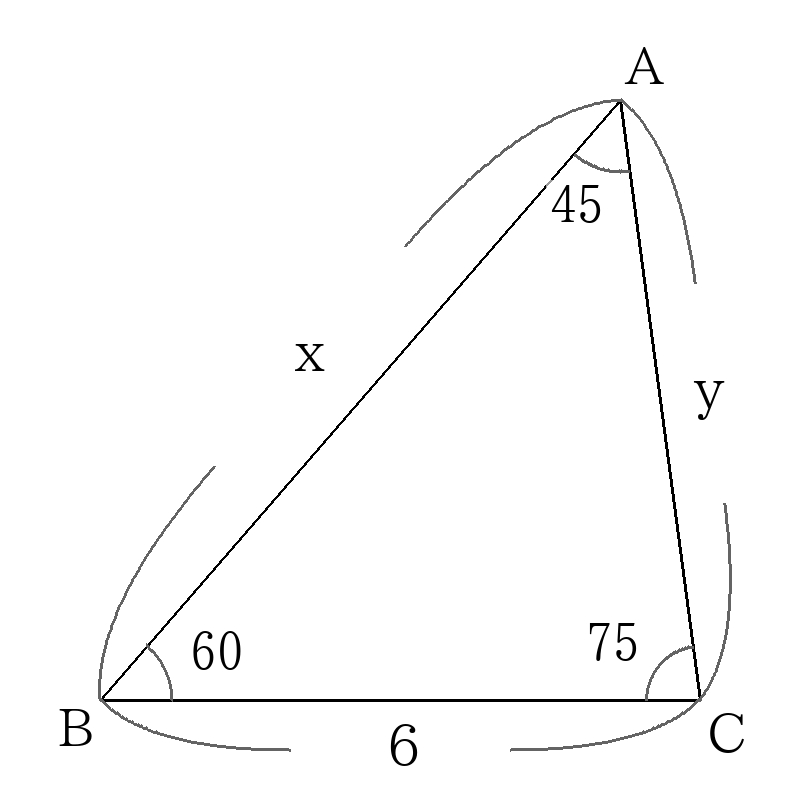
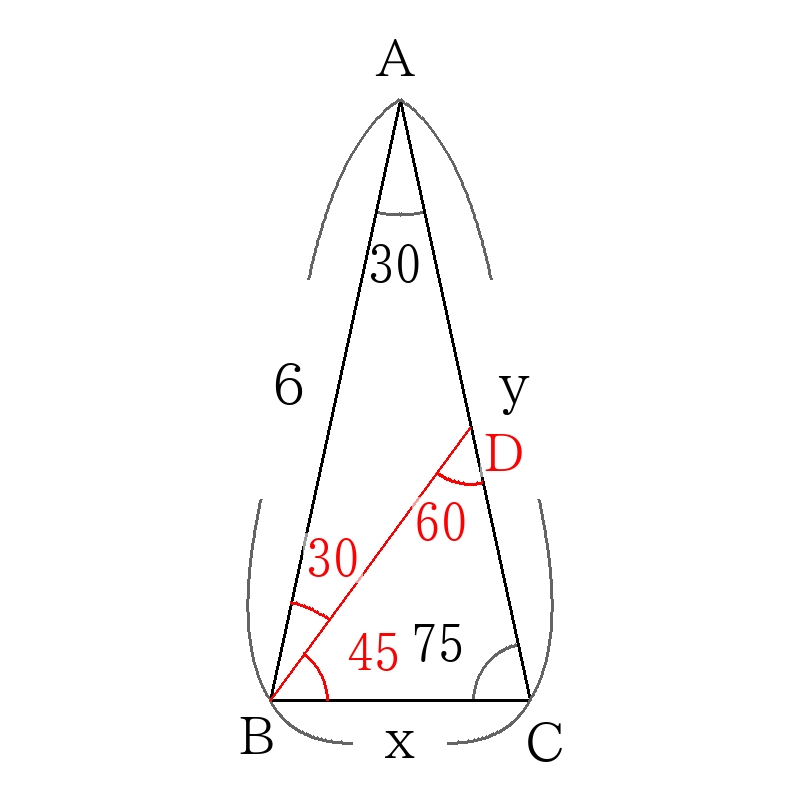
三角形\(ABC\)は\(AB=AC\)の二等辺三角形なので、
\(y=6 \)
図のように角\(B\)を30度と45度に分けるように直線\(BD\)を引く。
三角形\(BDC\)は(45度、60度、75度)の三角形なので辺の長さの比を書き入れる。
また、三角形\(ABD\)は\(AD=DB\)の二等辺三角形なので、
\(AD\)の長さの比は
\(AD=BD= \sqrt{3}+1 \)
よって
\(AC=AD+DC= \sqrt{3}+1+2= \sqrt{3}+3 \)
ここで、比の\( \left( \sqrt{3}+3 \right) \)にあたる長さが6なので、
\(x=6 \times \dfrac{ \sqrt{6}}{ \sqrt{3}+3} \)
\(x=3 \sqrt{6}-3 \sqrt{2} \)
\(x=3 \sqrt{6}-3 \sqrt{2},y=6 \)
【別解】
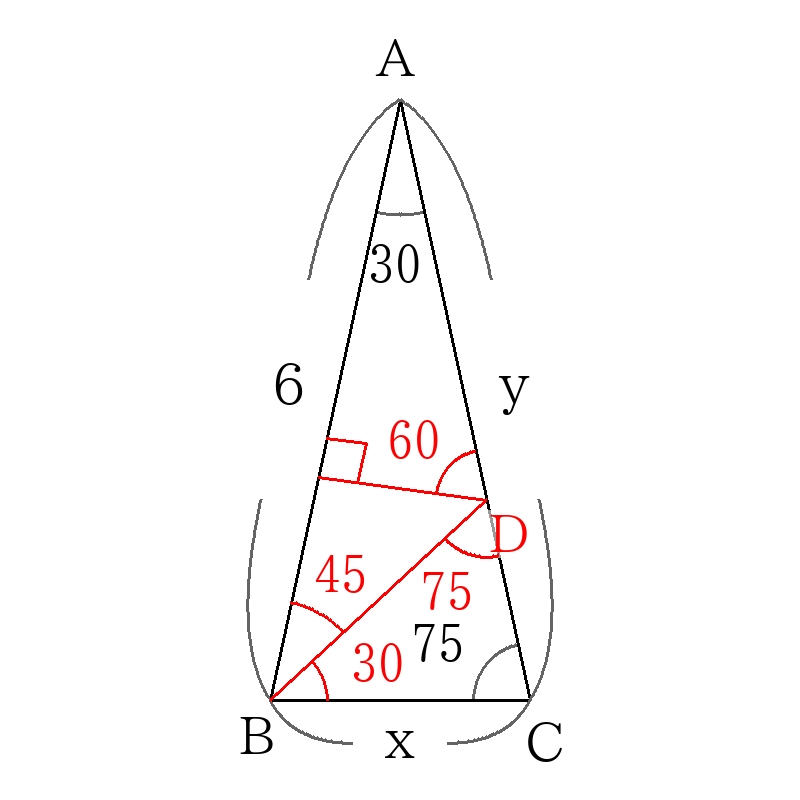

三角形\(ABC\)は\(AB=AC\)の二等辺三角形なので、
\(y=6 \)
図のように角\(B\)を30度と45度に分けるように直線\(BD\)を引き、\(D\)から\(AB\)に垂線を下す。
45°の直角二等辺三角形から辺の長さの比を書き入れる。
また、三角形\(ABD\)は\(AD=DB\)の二等辺三角形なので、
ここで、比の\( \left( \sqrt{3}+1 \right) \)にあたる長さが6なので、
\(x=6 \times \dfrac{ \sqrt{2}}{ \sqrt{3}+1} \)
\(x=3 \sqrt{6}-3 \sqrt{2} \)
\(x=3 \sqrt{6}-3 \sqrt{2},y=6 \)



コメント