基本知識
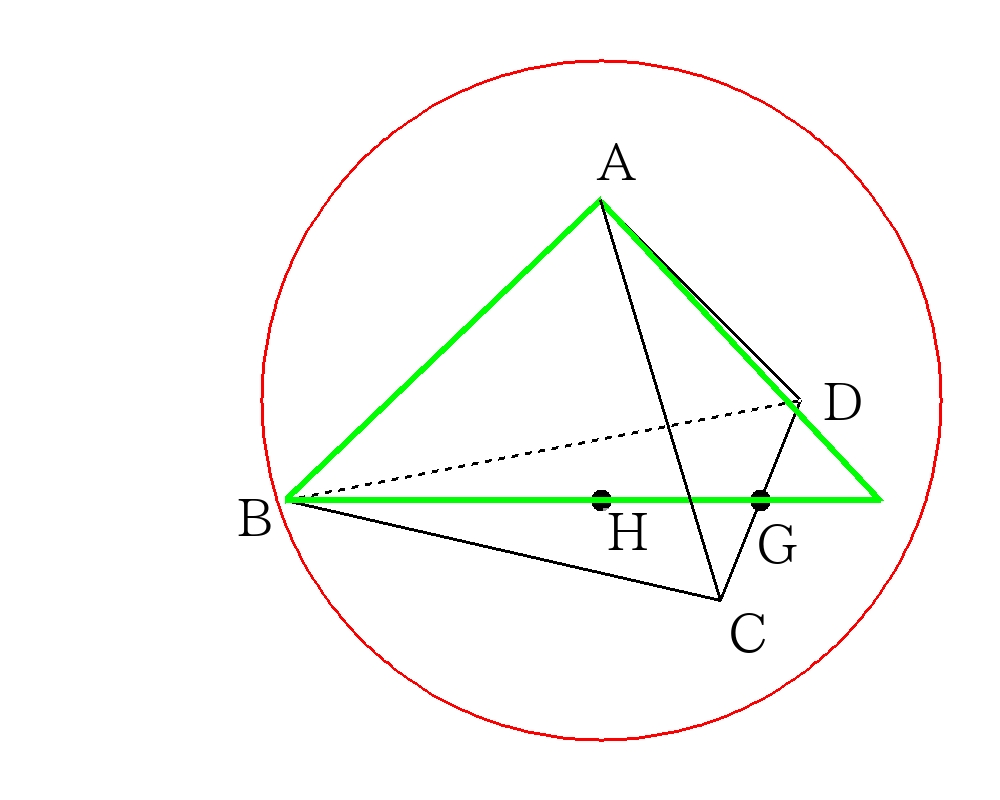
次の図のような1辺6㎝の正四面体\(ABCD\)があり、頂点\(A\)から面\(BCD\)に下した垂線を\(AH\)とする。これについて次の問いに答えなさい。
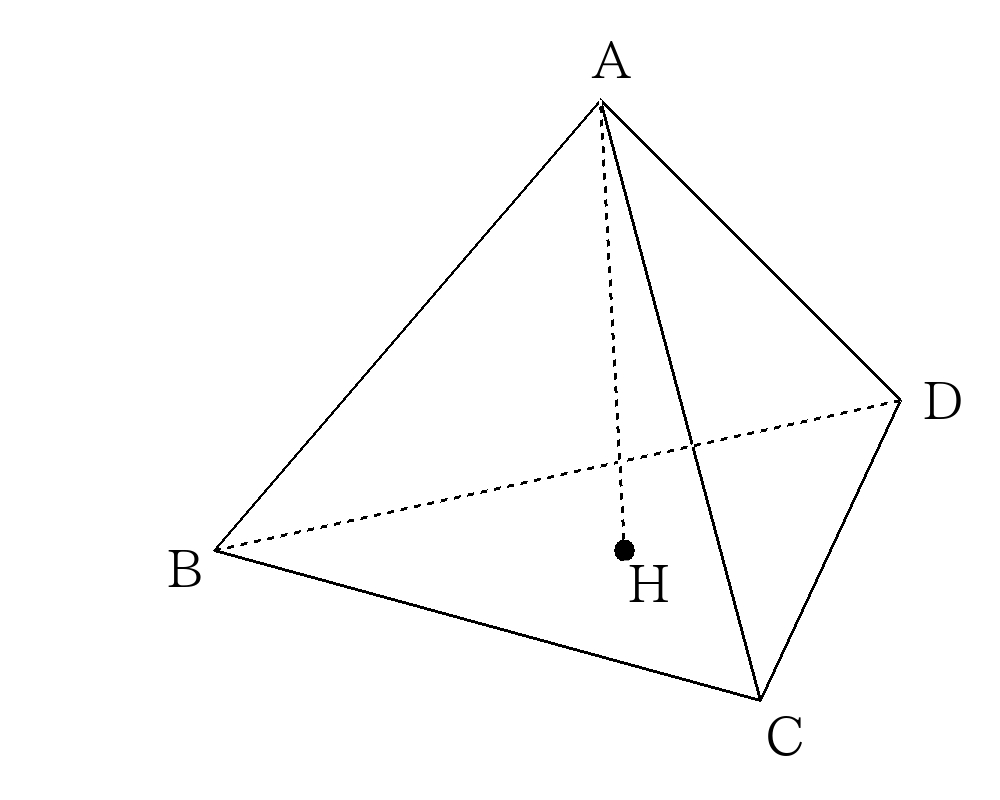
- 正四面体\(ABCD\)の表面積を求めなさい。
- \(AH\)の長さを求めなさい。
- 正四面体\(ABCD\)の体積を求めなさい。
- 正四面体\(ABCD\)に内接する球の半径を求めなさい。
- 正四面体\(ABCD\)に外接する球の半径を求めなさい。
1辺の長さが\(a\)の正四面体において
- 表面積=\(\sqrt{3}a^2\)
- 高さ=\(\dfrac{\sqrt{6}}{3}a\)
- 体積=\( \dfrac{ \sqrt{2} }{12}a^3 \)
- 内接球の半径=\( \dfrac{ \sqrt{6} }{12}a\)
- 外接球の半径=\( \dfrac{ \sqrt{6} }{4}a\)
※証明ができるようにしておくこと。※公式として覚えておくこと。
①表面積の求め方
それぞれの面は正三角形なので1つあたりの面積は\(\dfrac{\sqrt{3}}{4}a^2\)
それが4面あるので、表面積は\(\sqrt{3}a^2\)
②高さの求め方
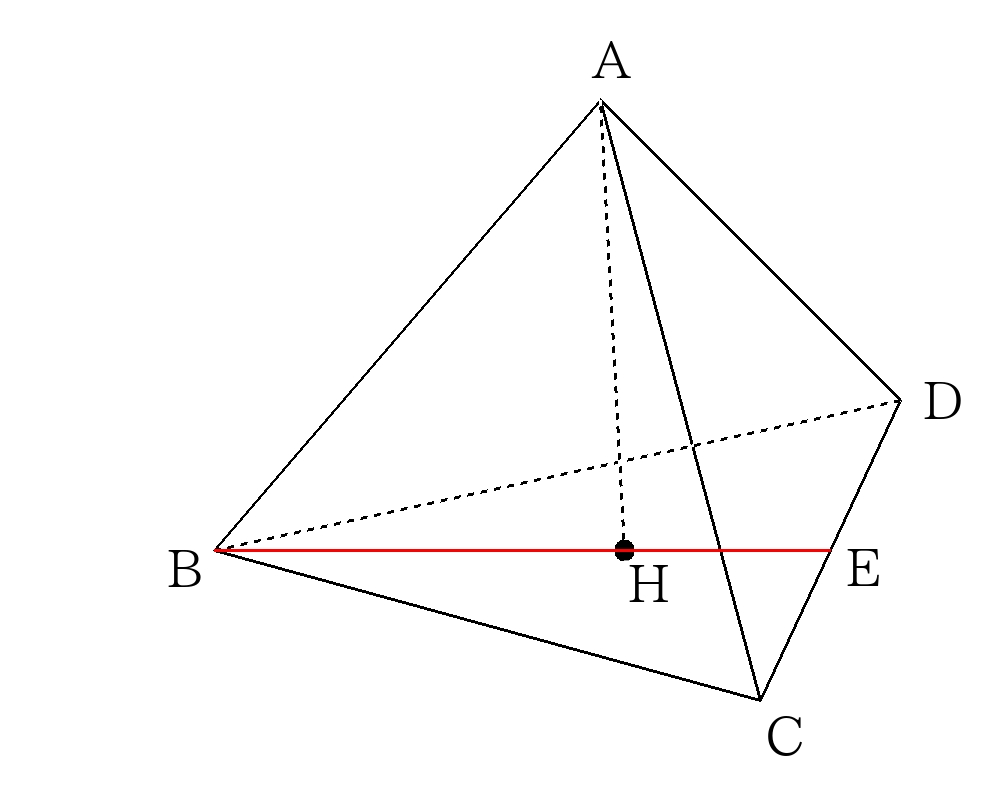
頂点\(B\)から辺\(CD\)に下した垂線を\(AE\)とする。\(H\)は\( \triangle ACD \)の重心なので、\(BH:HE=2:1\)
\(BE=\dfrac{\sqrt{3}}{2}a\)であり、\(BH=BE \times \dfrac{2}{2+1}=\dfrac{\sqrt{3}}{3}a \)
直角三角形\(ABH\)において三平方の定理より\(AH=\dfrac{\sqrt{6}}{3}a \)
③体積の求め方
底面積\(\triangle BCD=\dfrac{\sqrt{3}}{4}a^2\)、高さ\(AH=\dfrac{\sqrt{6}}{3}a \)より、
体積は\(\dfrac{\sqrt{3}}{4}a^2 \times \dfrac{\sqrt{6}}{3}a \times \dfrac{1}{3} = \dfrac{ \sqrt{2} }{12}a^3\)
③内接球の半径の求め方
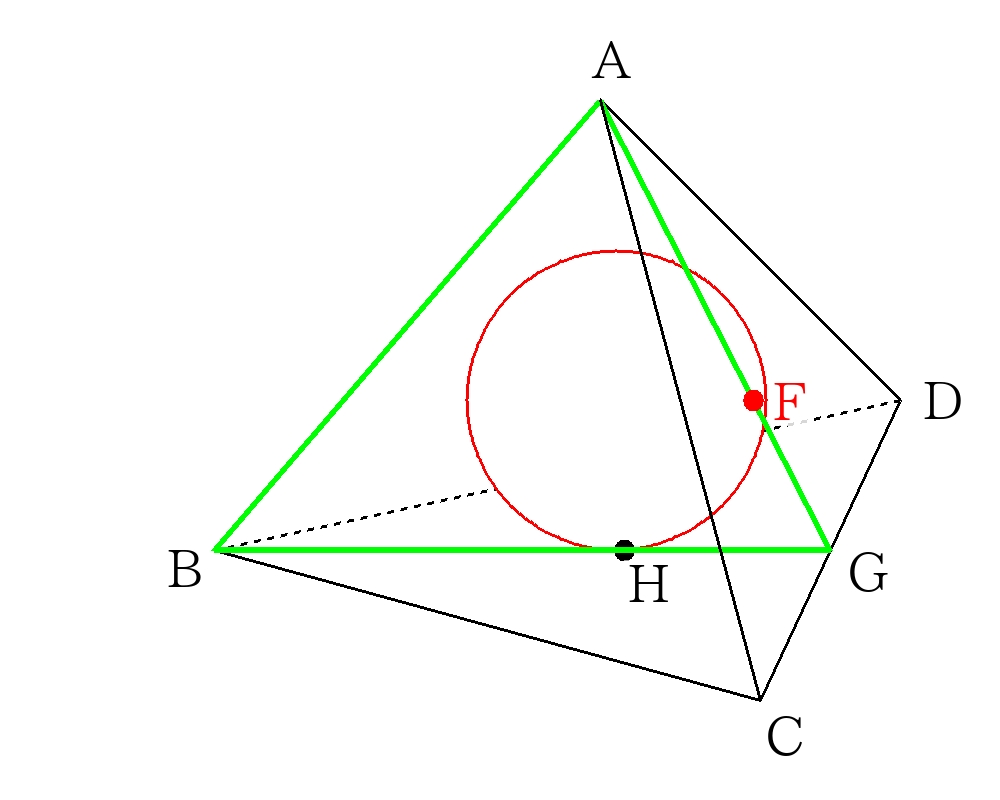
内接球は各面の正三角形の重心と接する。
\(\triangle ABG \)で切り出す。
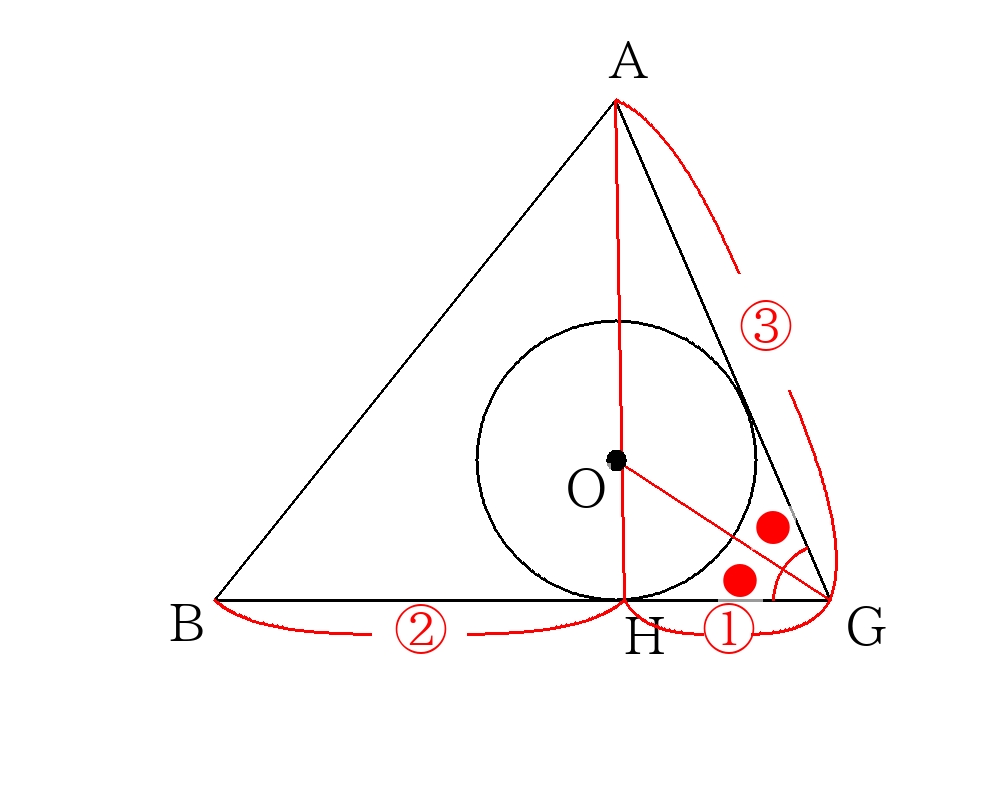
\(H\)は面\(BCD\)の重心であるため、\(BH:HG=2:1\)
また\(BG=AG\)のため、\(BH:HG:AG=2:1:3\)
1点から引いた2本の接線の性質から\( \angle AGD = \angle HGO \)であり、
角の二等分線の定理より\(AO:OH=3:1\)
\(AH=\dfrac{\sqrt{6}}{3}a \)とわかっているので
\(OH=AH \times \dfrac{1}{1+3}=\dfrac{\sqrt{6}}{3}a\times \dfrac{1}{4}=\dfrac{\sqrt{6}}{12}a\)
※内接球の半径の求め方として、体積と面積から逆算する方法も知っておくべき。
④外接球の半径の求め方
3点\(A,B,G\)を含む平面で切り抜く。
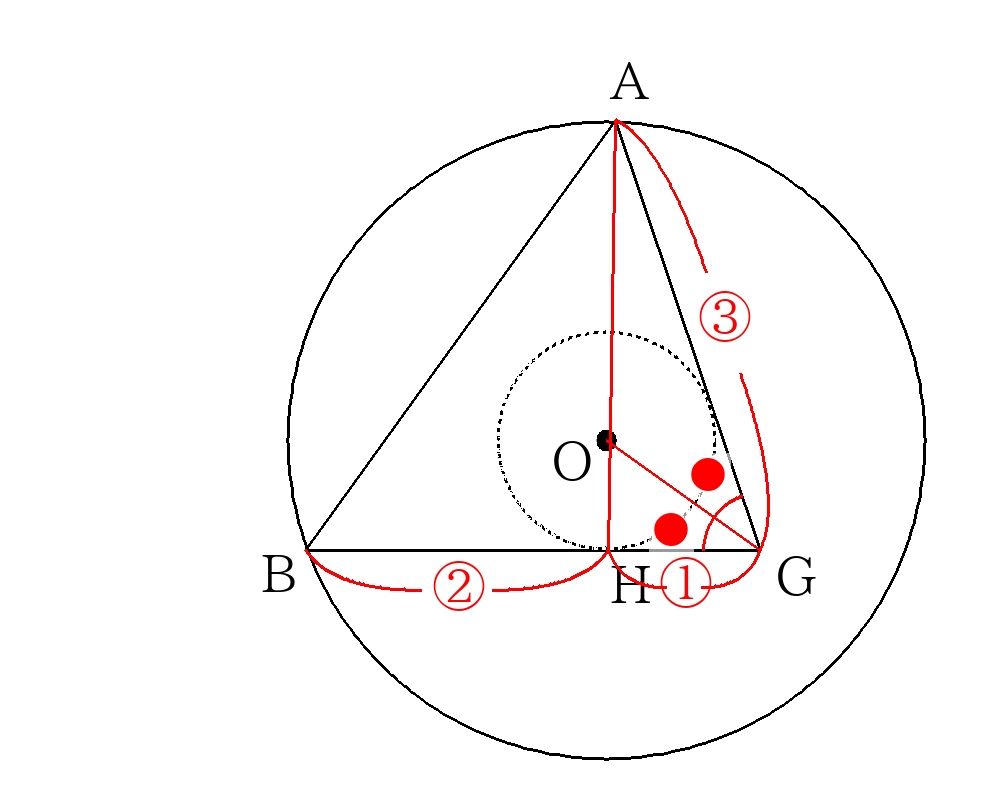
正四面体の内接球の中心と外接球の中心は一致する。内接球の半径を求めた関係を利用すると、
\(OA=AH \times \dfrac{3}{1+3}=\dfrac{\sqrt{6}}{3}a\times \dfrac{3}{4}=\dfrac{\sqrt{6}}{4}a\)
- 次の図のような1辺6㎝の正四面体\(ABCD\)があり、頂点\(A\)から面\(BCD\)に下した垂線を\(AH\)とする。これについて次の問いに答えなさい。
- 正四面体\(ABCD\)の表面積を求めなさい。
- \(AH\)の長さを求めなさい。
- 正四面体\(ABCD\)の体積を求めなさい。
- 正四面体\(ABCD\)に内接する球の半径を求めなさい。
- 正四面体\(ABCD\)に外接する球の半径を求めなさい。
以下、公式に当てはめて計算する。
\( \sqrt{3}a^2= \sqrt{3} \times 6^2=36 \sqrt{3} \)
\(36 \sqrt{3} \)
\( \dfrac{ \sqrt{6}}{3}a= \dfrac{ \sqrt{6}}{3} \times 6=2 \sqrt{6} \)
\(2 \sqrt{6} \)
\( \dfrac{ \sqrt{2}}{12}a^3= \dfrac{ \sqrt{2}}{12} \times 6^3=18 \sqrt{2} \)
\(18 \sqrt{2} \)
\( \dfrac{ \sqrt{6}}{12}a= \dfrac{ \sqrt{6}}{12} \times 6= \dfrac{ \sqrt{6}}{2} \)
\( \dfrac{ \sqrt{6}}{2} \)
\( \dfrac{ \sqrt{6}}{4}a= \dfrac{ \sqrt{6}}{4} \times 6= \dfrac{3 \sqrt{6}}{2} \)
\( \dfrac{3 \sqrt{6}}{2} \)



コメント