剰余の関係
- 15でも18でも割り切れる自然数のうち、3けたの自然数の個数を求めなさい。
- 6で割っても、9で割っても1あまる自然数のうち、2けたの自然数の個数を求めなさい。
- 24を割っても、36を割っても割り切れる自然数の個数を求めなさい。
- 45を割っても、60を割っても4あまる自然数を求めなさい。
- 200までの自然数のうち、3でも、5でも、7でも割り切れないの数の個数を求めなさい。
- 8で割ると5あまり、7で割ると6あまり、9で割ると1あまる自然数のうち5000に最も近い自然数を求めなさい。
- Aで割り切れる数=Aの倍数
AでもBでも割り切れる数=AとBの公倍数 - Aで割るとCあまる数=Aの倍数+C
※この条件を満たすN番目の自然数は、C+A×(N-1)の等差数列になる。
Aでも割ってもBで割ってもC余る数=AとBの公倍数+C - Aを割り切れる数=Aの約数
Aを割ってもBを割っても割り切れる数=AとBの公約数 - Aを割るとC余る数=(A-C)の約数のうちCより大きい数
Aを割ってもBを割ってもC余る数=(A-C)と(B-C)の公約数のうちCより大きい数
④について追加で説明すると、
例えば20を6で割ると2余ります。これは20個のお菓子を6人で分けると2個余るという意味です。
つまり、余りの2個を先に取り除いた(20-2=)18個であれば6人で割り切れるということです。
「余りを引けば割り切れる」と、覚えておいてください。
- 15でも18でも割り切れる自然数のうち、3けたの自然数の個数を求めなさい。
- 6で割っても、9で割っても1あまる自然数のうち、2けたの自然数の個数を求めなさい。
- 24を割っても、36を割っても割り切れる自然数の個数を求めなさい。
- 45を割っても、60を割っても4あまる自然数を求めなさい。
- 200までの自然数のうち、3でも、5でも、7でも割り切れないの数の個数を求めなさい。
- 8で割ると5あまり、7で割ると6あまり、9で割ると1あまる自然数のうち5000に最も近い自然数を求めなさい。
15と18の公倍数のうち、3けたの自然数を求めれば良い。
\(15と18の最小公倍数は90 \)
公倍数のうち小さい方からn番目の数は90nであり、これが3けたの条件を満たせば良いので、
\(100≦90n≦999 \)
\(1 \dfrac{1}{9}≦n≦11 \dfrac{1}{10} \)
この条件を満たすnはn=2からn=11まで
よって求める個数は
\(11-2+1=10 \)
※N=aからN=bを満たす自然数の個数を数えるときに両端の数を含む場合は(b-a+1)になるので注意すること。
\(10個 \)
6と9の公倍数に1を足した数のうち、、2けたの自然数を求めれば良い。
\(6と9の最小公倍数は18 \)
公倍数のうち小さい方からn番目の数は18nであり、それに1を足した数は18n+1、これが2けたの条件を満たせば良いので、
\(10≦18n+1≦99 \)
\(9≦18n≦98 \)
\( \dfrac{1}{2}≦n≦5 \dfrac{4}{9} \)
この条件を満たすnはn=1からn=5まで
よって求める個数は
\(5-1+1=5 \)
\(5個 \)
24と36の公約数を求めれば良い。
\(24と36の最大公約数は12 \)
\(12の約数は1,2,3,4,62の6個 \)
\(6個 \)
45と60の公約数のうち、4より大きい数を求めれば良い。
\(45と60の最大公約数は15 \)
\(15の約数は1,3,55 \)
このうち、割ったときに4余るのは
\(15の約数は55 \)
\(5,15 \)
3の倍数でも5の倍数でも7の倍数でもないものを数えれば良い。
それぞれの倍数において重複があるので、ベン図を利用して計算する。
3と5と7の公倍数=105の倍数、A=1個
5と7の公倍数=35の倍数、A+B=5個、B=4個
3と5の公倍数=15の倍数、A+C=13個、C=12個
3と7の公倍数=21の倍数、A+D=9個、D=8個
3の倍数、A+C+D+G=66個、D=45個
5の倍数、A+B+C+E=40個、E=23個
7の倍数、A+B+D+F=28個、F=15個
よって求めるべき個数Hは200-(A+B+C+D+E+F)=200-108=92
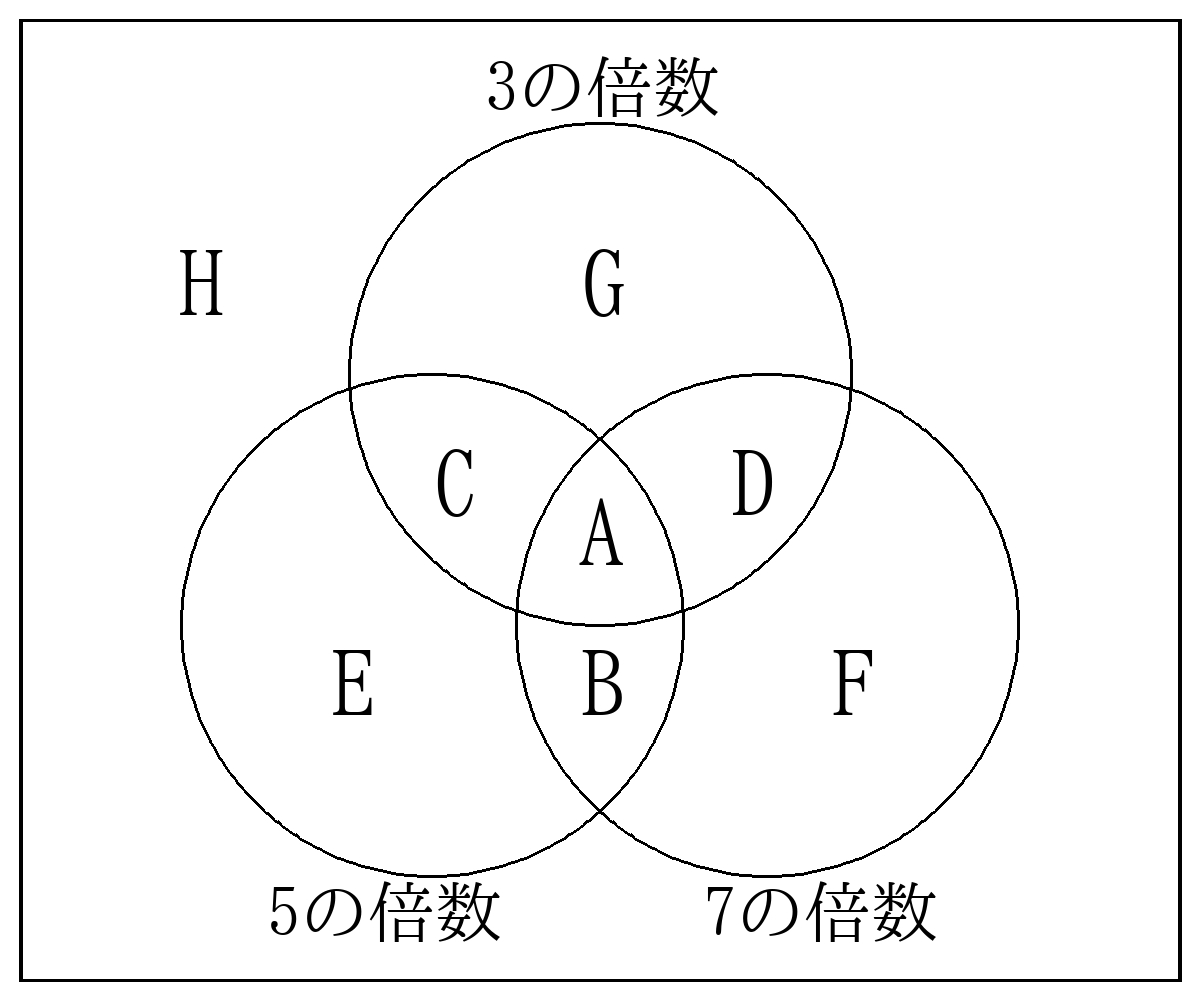
ベン図はさまざまな計算方法がある。中心から埋めるのが一番確実な方法。
重なりを理解している人は、(66+40+28)-(5+13+9)+1=108から計算すれば良い。
\(92個 \)
それぞれ\(5+8(N-1)\)、\(6+7(N-1)\)、\(7+9(N-1)\)で表される等差数列のため、一致する数を求めれば良い。
まず\(5+8(N-1)\)、\(6+7(N-1)\)の2つが一致する数を求めるために、数列を書き出すと、
\(5+8(N-1)→53,21,29,37,45 \dots \)
\(6+7(N-1)→63,20,27,34,41 \dots \)
この2つの数列は13ではじめに一致し、その後は(8と7の最小公倍数=)56ずつ増える数列(\(13+56(N-1)\))になる。
この数列のうち、9で割ると1あまる数を求められば良いので、順に書き出して調べる。
\(13+56(N-1)→13,692581,237 \dots \)
13は9で割るとあまり4なので不適、69は9で割るとあまり6なので不適、・・・181は9で割るとあまり1で一致する。
よって求めるべき数列は、はじめの数が181で(8と7と9の最小公倍数=)504ずつ増える等差数列(\(181+504(N-1)\))である。
あとは\(5000\)に近い数を求めれば良い。
\(N=9\)のとき\(181+504 \times (9-1)=4717\)であり\(5000\)との差は\(283\)
\(N=10\)のとき\(181+504 \times (10-1)=5221\)であり\(5000\)との差は\(221\)
※最も近い数を求めるときはそれよりも小さい数と大きい数の両方を検証しなければならない。
よって、\(5221\)が\(5000\)に最も近い。
\(5221 \)



コメント