辺の比の利用
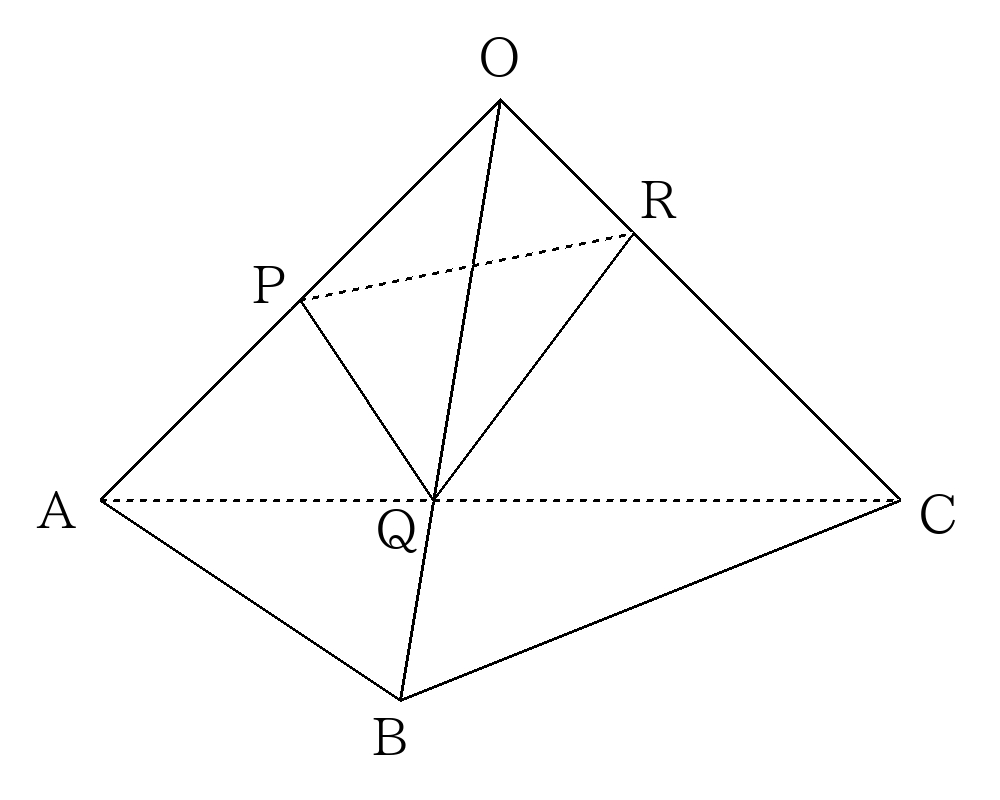
- 次の図のような三角錐\(O-ABC\)があり、
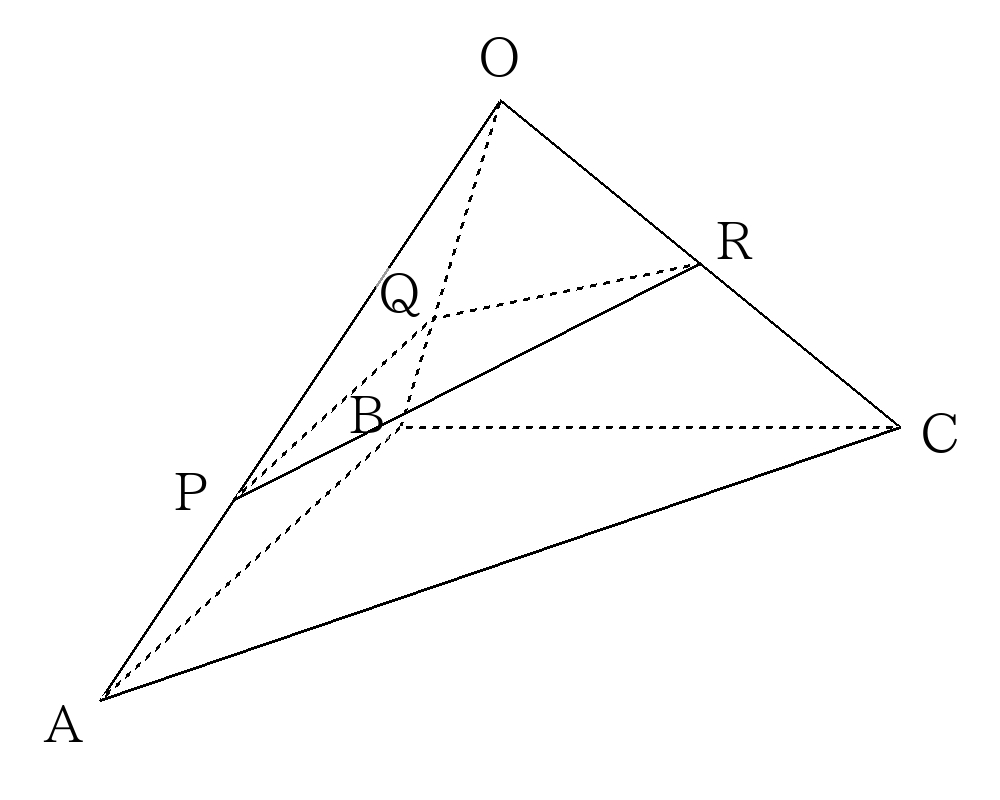
\(OP:PA=1:1\)、\(OQ:QB=2:1\)、\(OR:RC=1:2\)である。この三角錐を3点\(P、Q、R\)を通る平面で切断したとき、立体\(O-PQR\)の体積は三角錐\(O-ABC\)の体積の何倍か求めなさい。
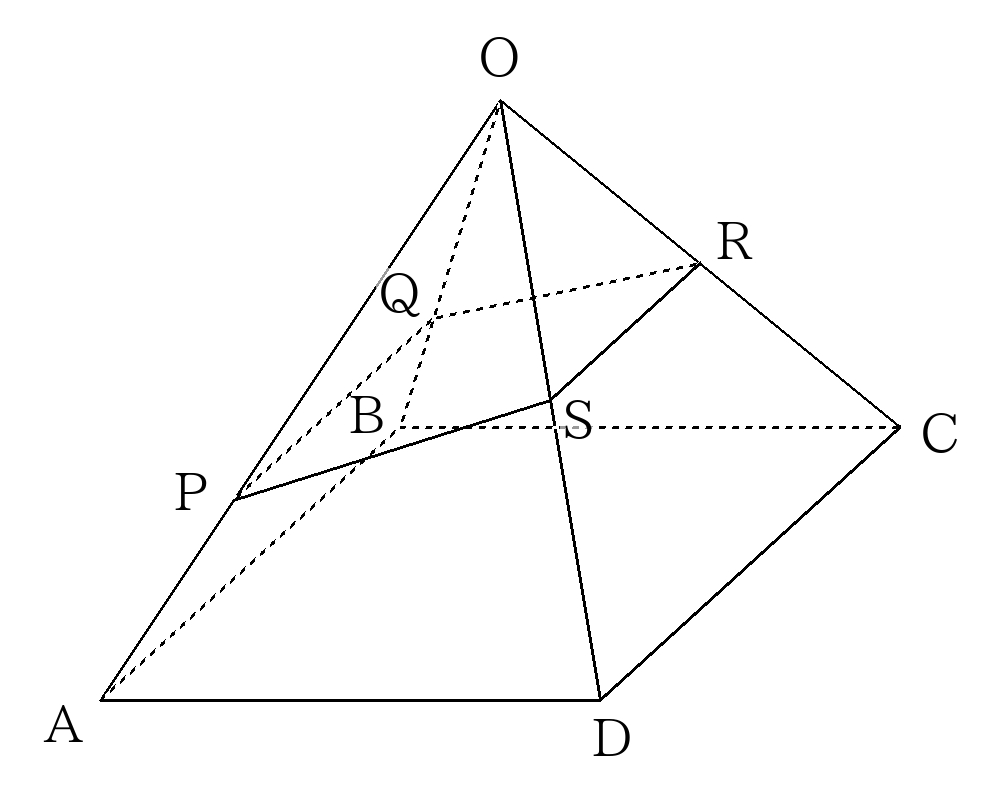
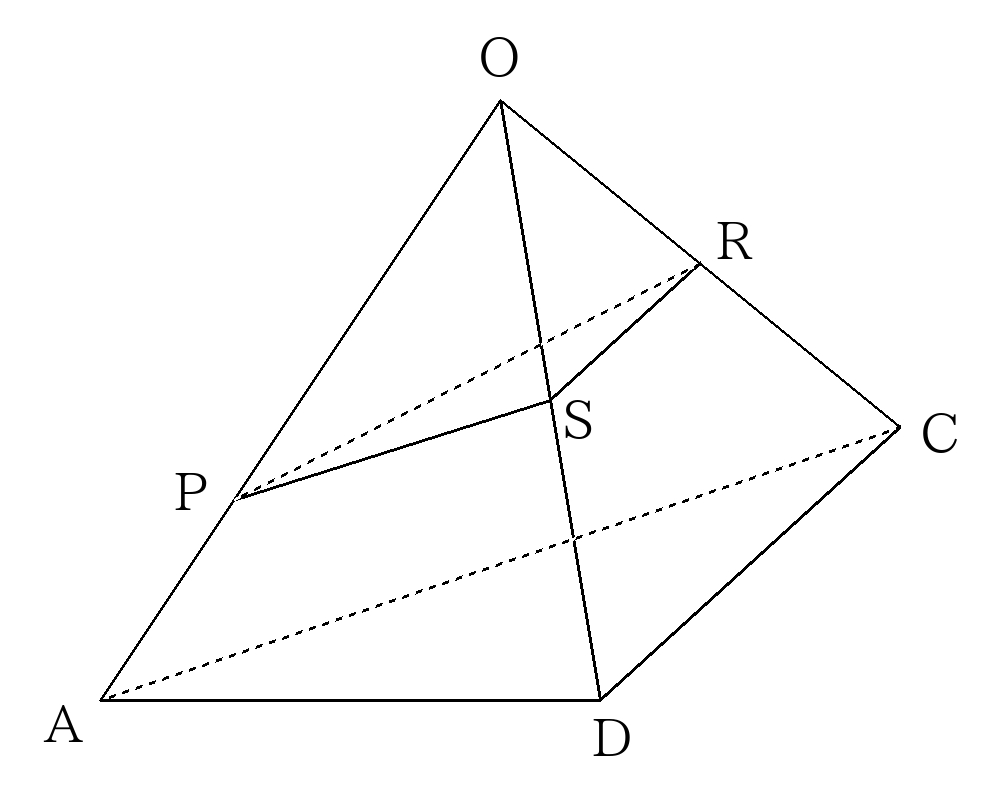
- 次の図のような正四角錐\(O-ABCD\)があり、\(OP:PA=OQ:QB=2:1\)、\(OS:SD=OR:RC=1:1\)である。この四角錐を4点\(P、Q、R、S、\)を通る平面で切断したとき、
立体\(O-PQRS\)の体積は四角錐\(O-ABCD\)の何倍か求めなさい。
- 三角錐の切断は以下の公式が成り立つ。
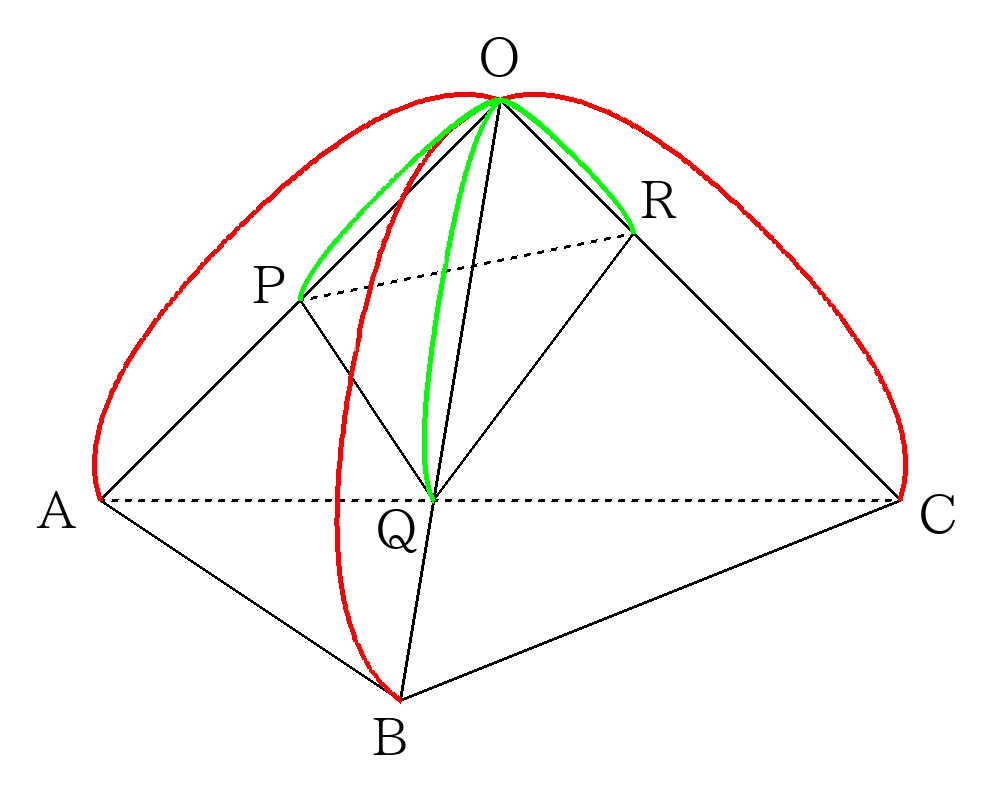
\( (O-PQRの体積)=\)\((O-ABCの体積) \times \dfrac{\color{ green }{ OP } }{ \color{ #ff0000 }{OA} } \times \dfrac{\color{ green }{ OQ }}{ \color{ #ff0000 }{ OB } } \times \dfrac{\color{ green }{ OR }}{ \color{ #ff0000 }{OC}} \)
\( (O-ABCの体積):(O-PQRの体積) \)\( =\color{ #ff0000 }{ OA } \times \color{ #ff0000 }{ OB } \times \color{ #ff0000 }{ OC }:\color{ green }{ OP } \times \color{ green }{ OQ } \times \color{ green }{ OR } \) - 四角錐は2つの三角錐に分けろ
証明は省略するが、面積が2辺の比より決まり、高さの比が残りの1辺の比によって決まることから証明できる。
- 次の図のような三角錐\(O-ABC\)があり、
\(OP:PA=1:1\)、\(OQ:QB=2:1\)、\(OR:RC=1:2\)である。この三角錐を3点\(P、Q、R\)を通る平面で切断したとき、\(O-PQR\)の体積は三角錐\(O-ABC\)の体積の何倍か求めなさい。 - 次の図のような正四角錐\(O-ABCD\)があり、\(OP:PA=OQ:QB=2:1\)、\(OS:SD=OR:RC=1:1\)である。この四角錐を4点\(P、Q、R、S、\)を通る平面で切断したとき、
立体\(O-PQRS\)の体積は四角錐\(O-ABCD\)の何倍か求めなさい。
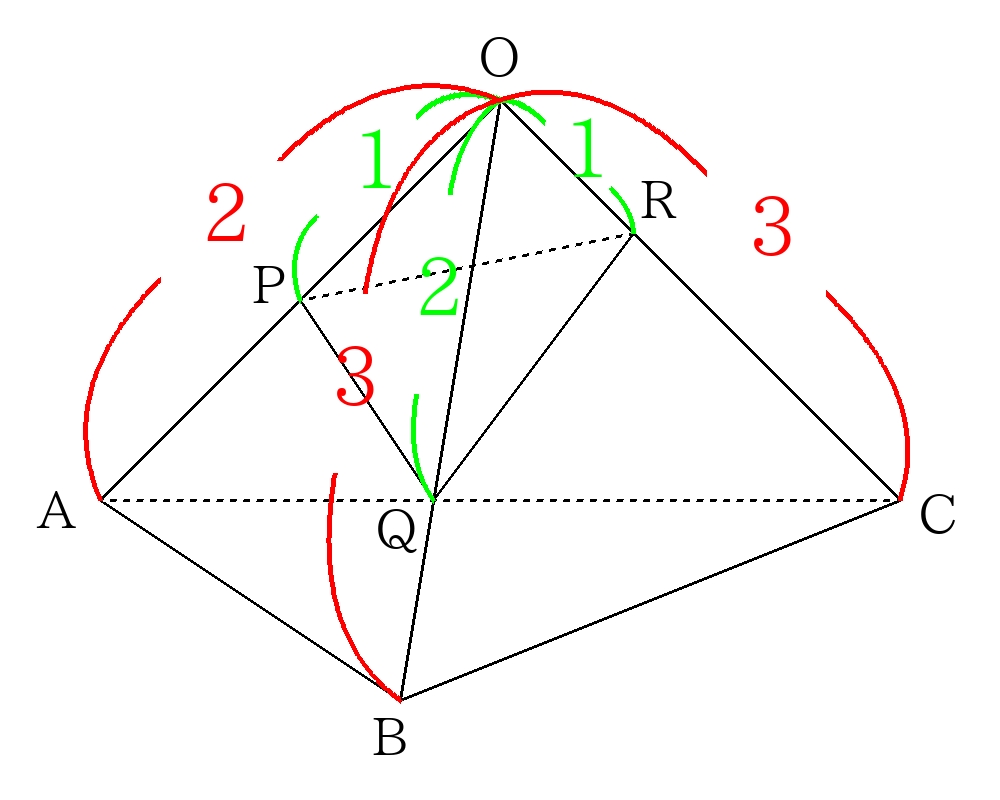
三角錐の切断の公式より
\((O-PQRの体積)=(O-ABCの体積) \times \dfrac{1}{2} \times \dfrac{2}{3} \times \dfrac{1}{3} \)
\((O-PQRの体積)=(O-ABCの体積) \times \dfrac{1}{9} \)
\( \dfrac{1}{9}倍 \)
四角錐を\(OAC\)の平面で2つの三角錐に分ける。
三角錐の切断の公式より
\((O-PQRの体積)=(O-ABCの体積) \times \dfrac{2}{3} \times \dfrac{2}{3} \times \dfrac{1}{2} \)
\(=(O-ABCの体積) \times \dfrac{2}{9} \)
\(=(O-ABCDの体積) \times \dfrac{1}{2} \times \dfrac{2}{9} \)
\(=(O-ABCDの体積) \times \dfrac{1}{9} \)
また
\((O-PSRの体積)=(O-ADCの体積) \times \dfrac{2}{3} \times \dfrac{1}{2} \times \dfrac{1}{2} \)
\(=(O-ADCの体積) \times \dfrac{1}{6} \)
\(=(O-ABCDの体積) \times \dfrac{1}{2} \times \dfrac{1}{6} \)
\(=(O-ABCDの体積) \times \dfrac{1}{12} \)
よって
\((O-PQRSの体積)=(O-PSRの体積)+(O-PQRの体積) \)
\(=(O-ABCDの体積) \times \left( \dfrac{1}{9}+ \dfrac{1}{12} \right) \)
\(=(O-ABCDの体積) \times \dfrac{7}{36} \)
\( \dfrac{7}{36}倍 \)



コメント