内接円と外接円
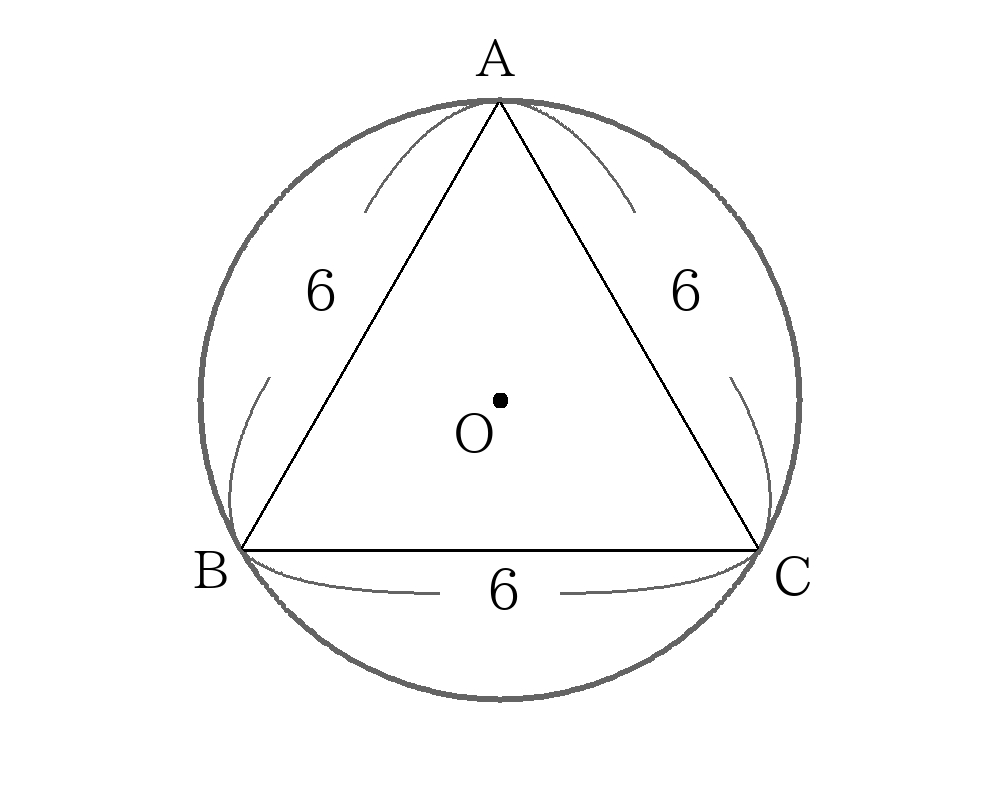
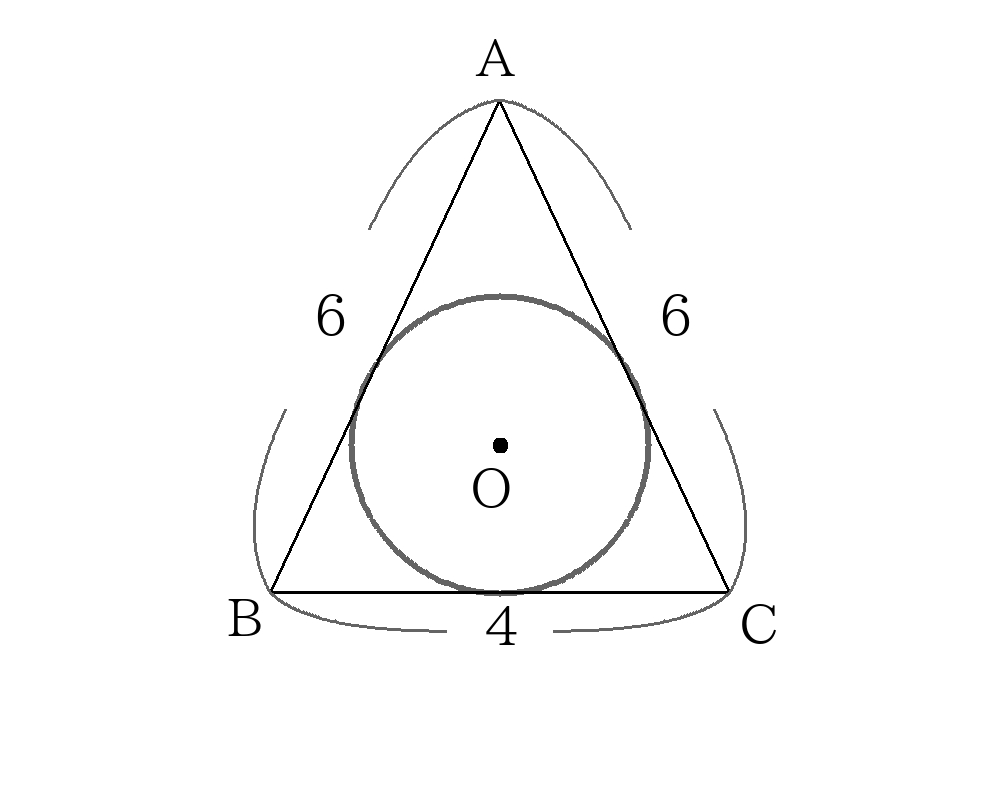
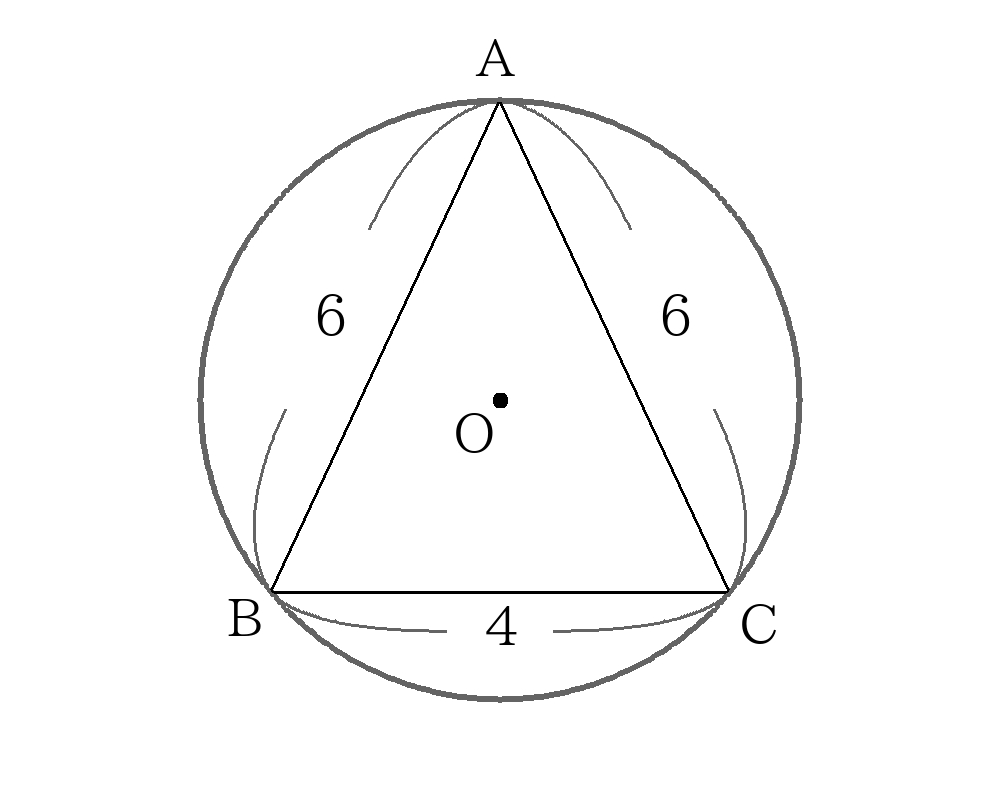
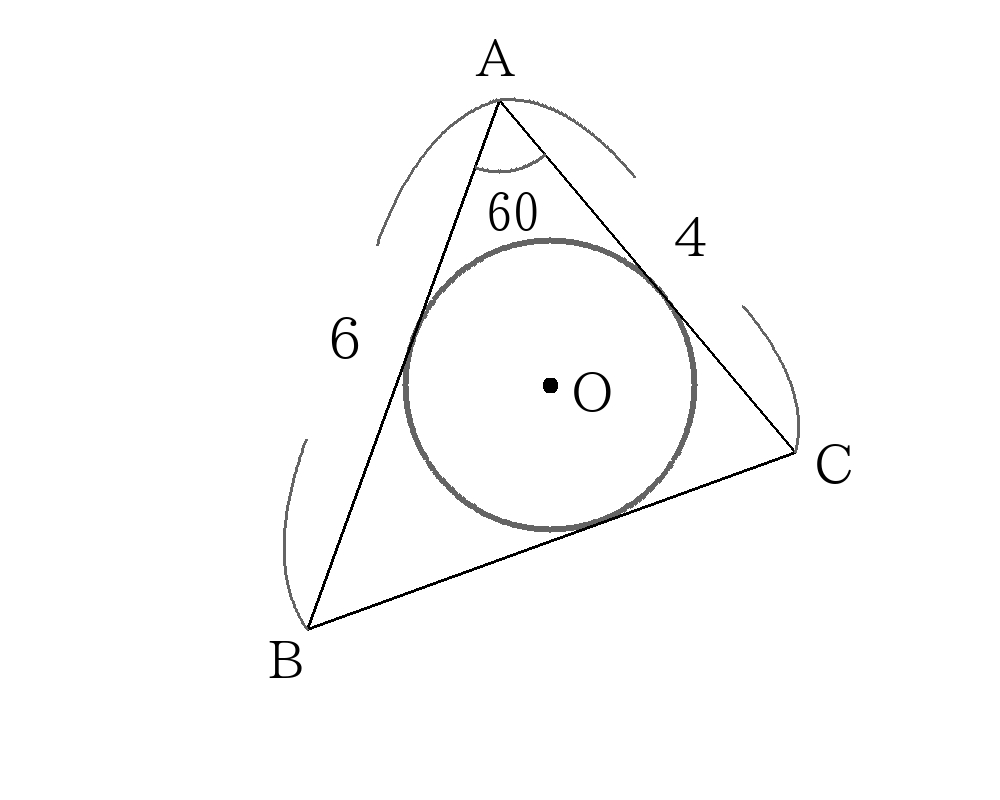
次の図の内接円の半径\(r\)、外接円の半径\(R\)を求めなさい。
内接円の半径の求め方
- 面積を2通りで表して求める。
- (相似や三平方の定理を利用する。)
外接円の半径の求め方
- 直径となる補助線を引き、直角三角形の相似形で計算する。
- (特別角が与えられたら中心角を作って計算する。)
- (相似や三平方の定理を利用する。)
※( )内の解き方のようにさまざまな工夫ができる。
※原理原則を抑えつつ問題演習でコツをつかんでほしい。
内接円の基本解法(面積を2通りで計算)
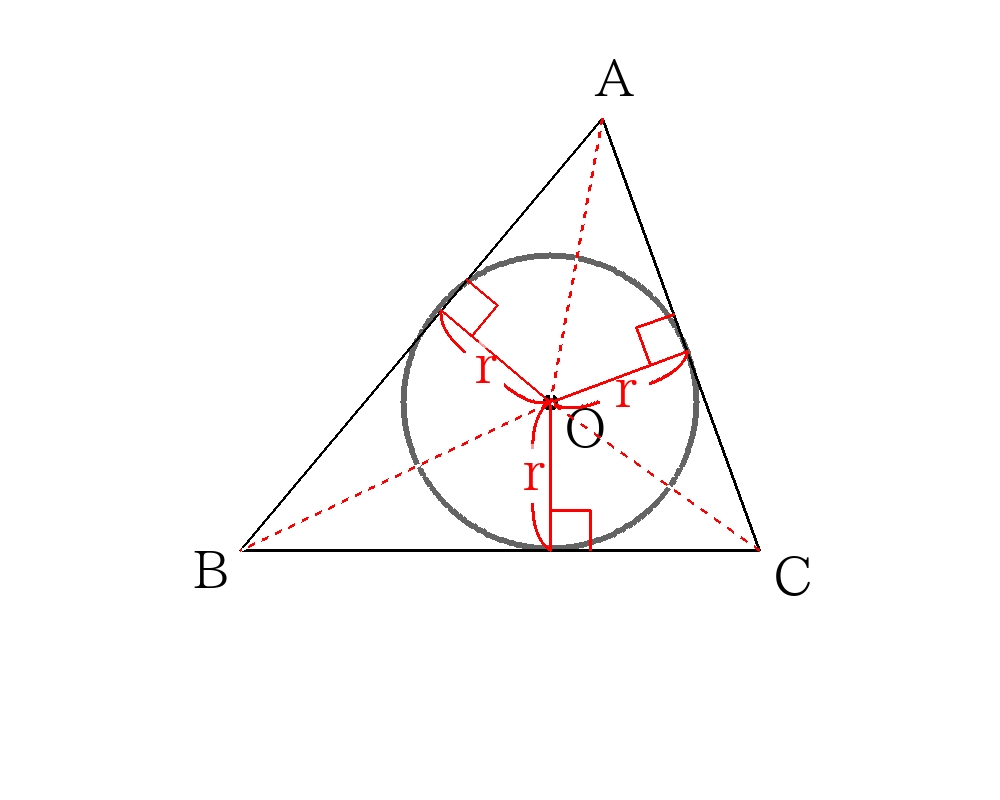
①三角形の面積\(S\)を三平方の定理から求める。詳しくは三平方の定理を参照
②また上の図より三角形の面積\(S\)は3つの三角形の面積の和として求められるので
\(S=AB \times r \times \dfrac{1}{2} + BC \times r \times \dfrac{1}{2} + AC \times r \times \dfrac{1}{2} \)
\(S=(AB+BC+AC) \times r \times \dfrac{1}{2}\)
\(r= \dfrac{2S}{AB+BC+AC}\)
外接円の基本解法(直径となる補助線)
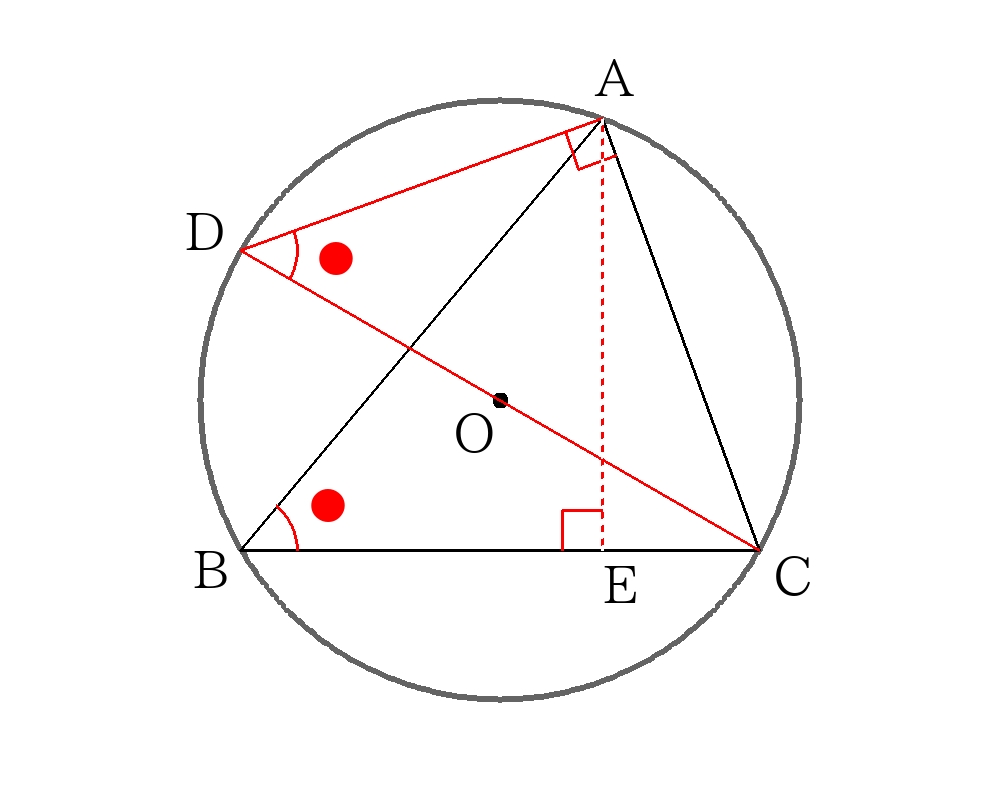
頂点\(A\)を通る\(BC\)の垂線\(AE\)を引き、\(AE\)の長さを三平方の定理から計算する。
図のように直径\(CD\)を引く。
\( \triangle ABE\)∽\(\triangle CDA \)より
\(EA:AB=AC:CD\)
ここで\(CD=2R\)なので、
\(EA:AB=AC:2R\)
\(2R= \dfrac{(AB) \times(AC)}{EA}\)
※式を覚えるのではなく解き方の流れを身に付けること。
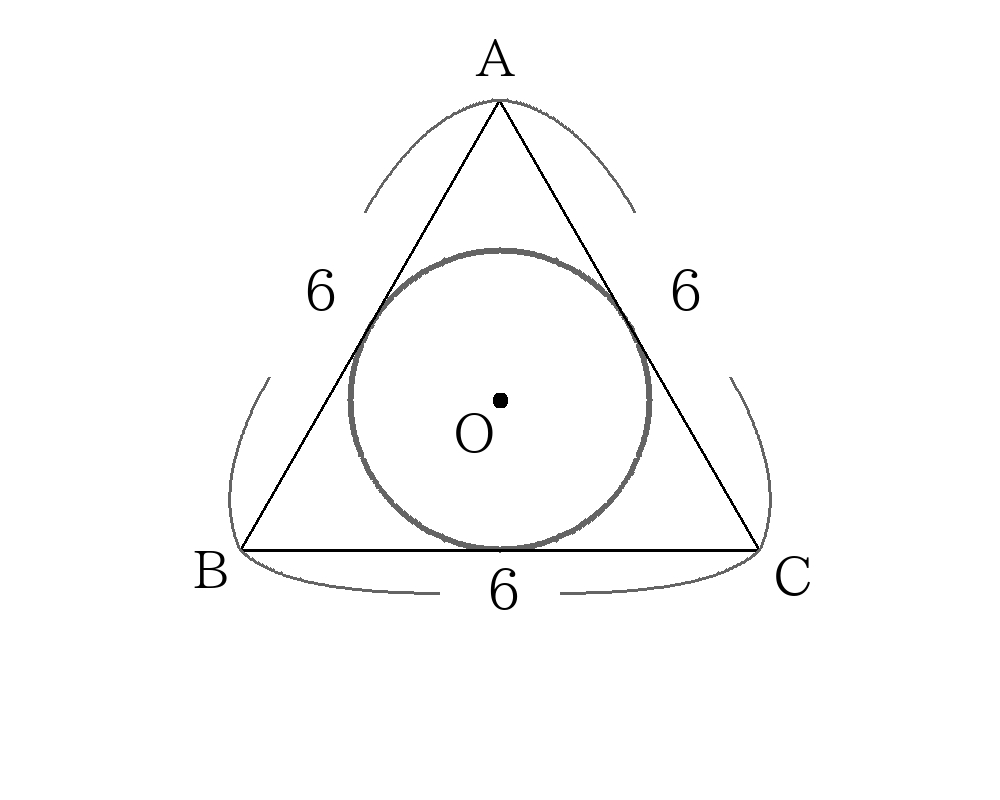
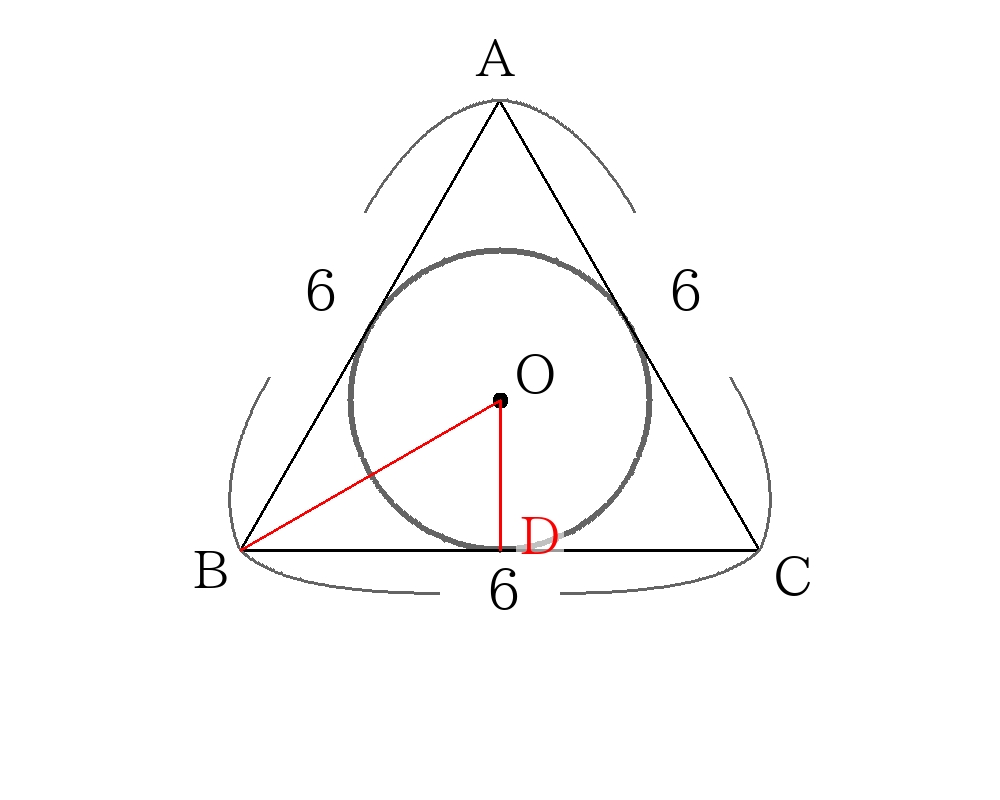
内接円の解き方① 面積から求める。
正三角形\(ABC\)の面積\(S\)は三平方の定理を利用すると、
\(S=9 \sqrt{3} \dots① \)
また、内接円の半径\(r\)を用いて
\(S= \dfrac{1}{2}r(AB+BC+AC) \)
\(S=9r \dots② \)
①,②より
\(r= \sqrt{3} \)
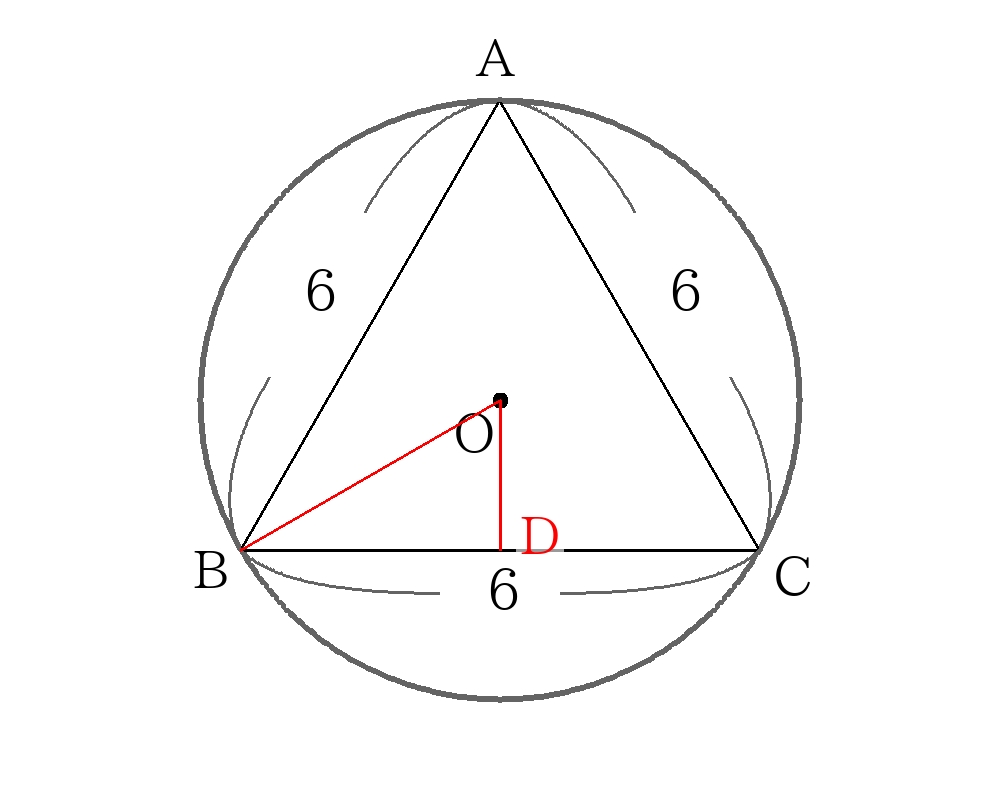
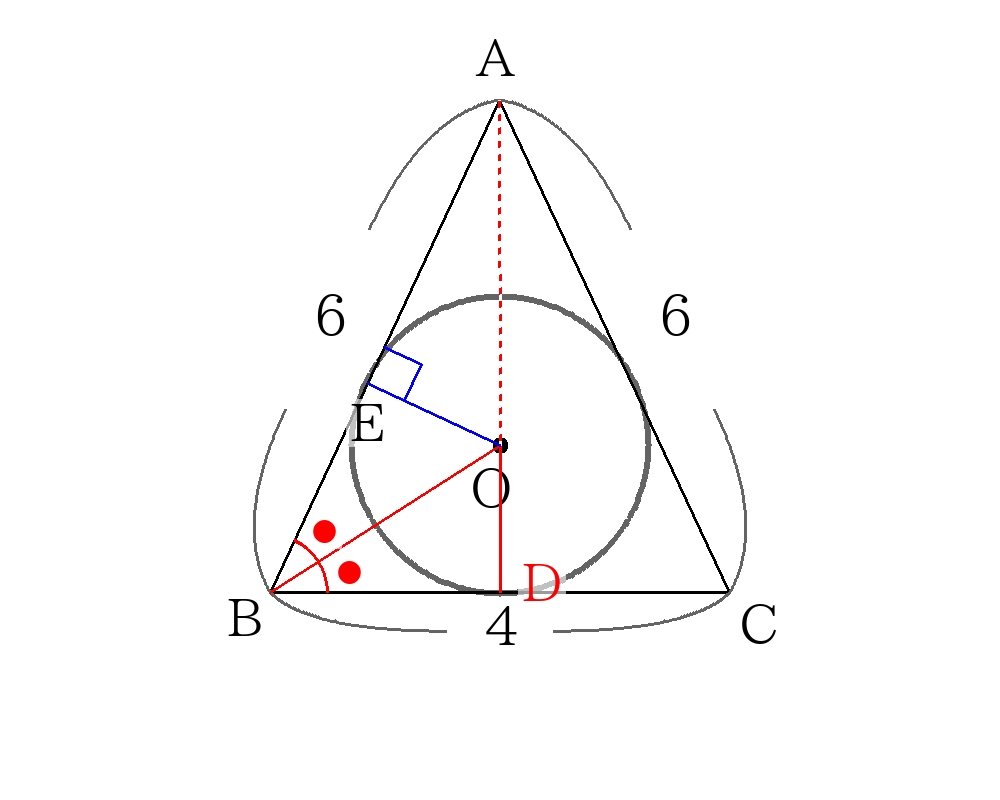
内接円の解き方② 特別角の三平方の定理から求める。
\(O\)から\(BC\)に垂線\(OD\)を引くと、\(\triangle DOB\)は\(DO:OB:BD=1:2:\sqrt{3}\)の直角三角形なので、
\(OD:DB=r:3=1: \sqrt{3} \)
\( \sqrt{3}r=3 \)
\(r= \sqrt{3} \)
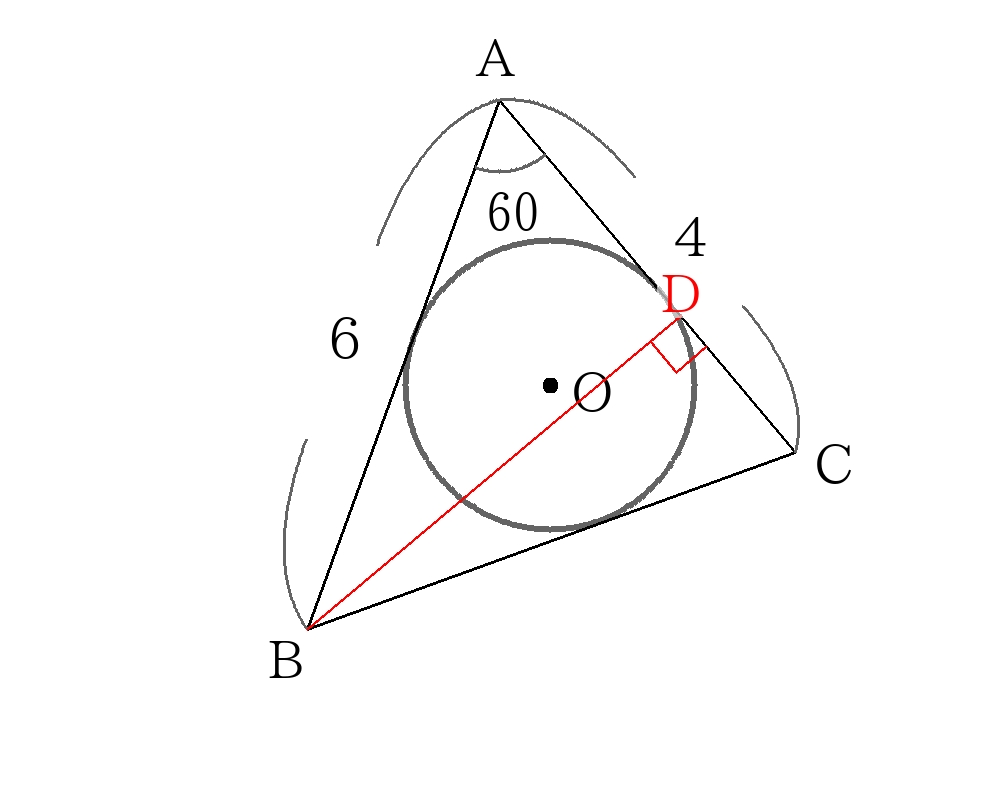
外接円の解き方 特別角の三平方の定理から求める。
\(O\)から\(BC\)に垂線\(OD\)を引くと、\(\triangle DOB\)は\(DO:OB:BD=1:2:\sqrt{3}\)の直角三角形なので、
\(BD:OB=3:R= \sqrt{3}:2 \)
\( \sqrt{3}R=6 \)
\(R=2 \sqrt{3} \)
内接円の解き方① 面積から求める。
正三角形\(ABC\)の面積\(S\)は三平方の定理を利用すると、
\(S=8 \sqrt{2} \dots① \)
また、内接円の半径\(r\)を用いて
\(S= \dfrac{1}{2}r(AB+BC+AC) \)
\(S=8r \dots② \)
①,②より
\(r= \sqrt{2} \)
内接円の解き方② 角の二等分線の利用
\(O\)から\(BC\)に垂線\(OD\)を引くと、\(OB\)が\(\angle ABC\)の二等分線になる。(1点から引いた2つの接線の長さは等しい。)
角の二等分線の定理より、
\(AO:OD=6:2=3:1 \)
よって
\(OD=AD \times \dfrac{1}{3+1}=4 \sqrt{2} \times \dfrac{1}{4}= \sqrt{2} \)
\(r= \sqrt{2} \)
内接円の解き方③ 相似の利用
\(O\)から\(AB\)に垂線\(OE\)を引き、\( \triangle AOE \)∽\( \triangle ABD \)を利用する。
\(OD=r\)とすると、\(AO=4 \sqrt{2}-r\)
\(AO:OE=AB:BD\)より
\( \left(4 \sqrt{2}-r \right):r=6:2 \)
\(r= \sqrt{2} \)
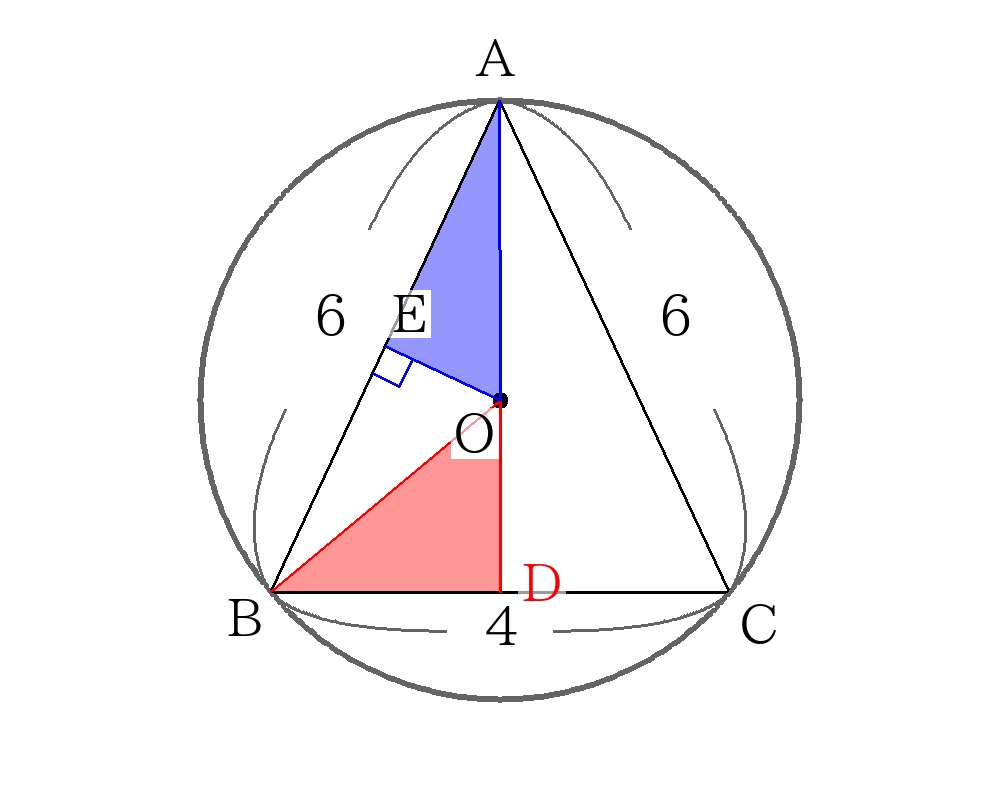
外接円の解き方 二等辺三角形と三平方の定理
\(A\)から\(BC\)に垂線\(AD\)を引くと、\(\triangle ADB\)の三平方の定理より\(AD=4 \sqrt{2}\)
\(AO=BO=R\)であり、\(\triangle ODB\)の三平方の定理より、
\( \left(4 \sqrt{2}-R \right)^2+2^2=R^2 \)
\(8 \sqrt{2}R=36 \)
\(R= \dfrac{9 \sqrt{2}}{4} \)
外接円の解き方 相似の利用
\(A\)から\(BC\)に垂線\(AD\)を引くと、\(\triangle ADB\)の三平方の定理より\(AD=4 \sqrt{2}\)
\(O\)から\(AB\)に垂線\(OE\)を引くと\(AE=BE=3\)、\(\triangle AOE\)∽\(\triangle ABD\)より
\(AO:AE=AB:AD \)
\(R:3=6:4 \sqrt{2} \)
\(4 \sqrt{2}R=18 \)
\(R= \dfrac{9 \sqrt{2}}{4} \)
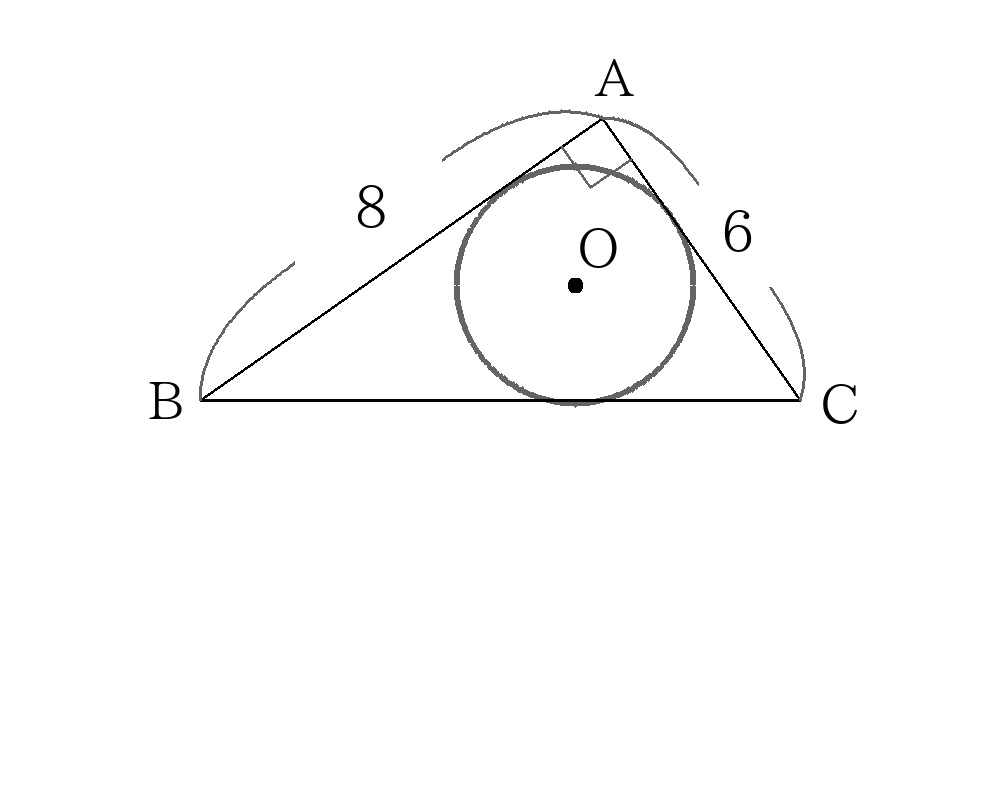
内接円の解き方 面積から求める。
\(AC\)に垂線\(BD\)を下す。
正三角形\(ABD\)は30度、60度の直角三角形で辺の比が\(1:2:\sqrt{3}\)なので、
\(BD=6 \times \dfrac{ \sqrt{3}}{2}=3 \sqrt{3} \)
\(AD=6 \times \dfrac{1}{2}=3 \)
\(CD=AC-AD=1 \)
直角三角形\(DBC\)において三平方の定理より
\(BC^2= \left(3 \sqrt{3} \right)^2+1^2 \)
\(BC>0\)より
\(BC=2 \sqrt{7} \)
よって三角形\(ABC\)の面積\(S\)は
\(S=4 \times 3 \sqrt{3} \times \dfrac{1}{2}=6 \sqrt{3} \dots① \)
\(S= \dfrac{1}{2}r \left(4+6+2 \sqrt{7} \right) \dots② \)
①,②より
\( \left(5+ \sqrt{7} \right)r=6 \sqrt{3} \)
\(r= \dfrac{5 \sqrt{3}- \sqrt{21}}{3} \)
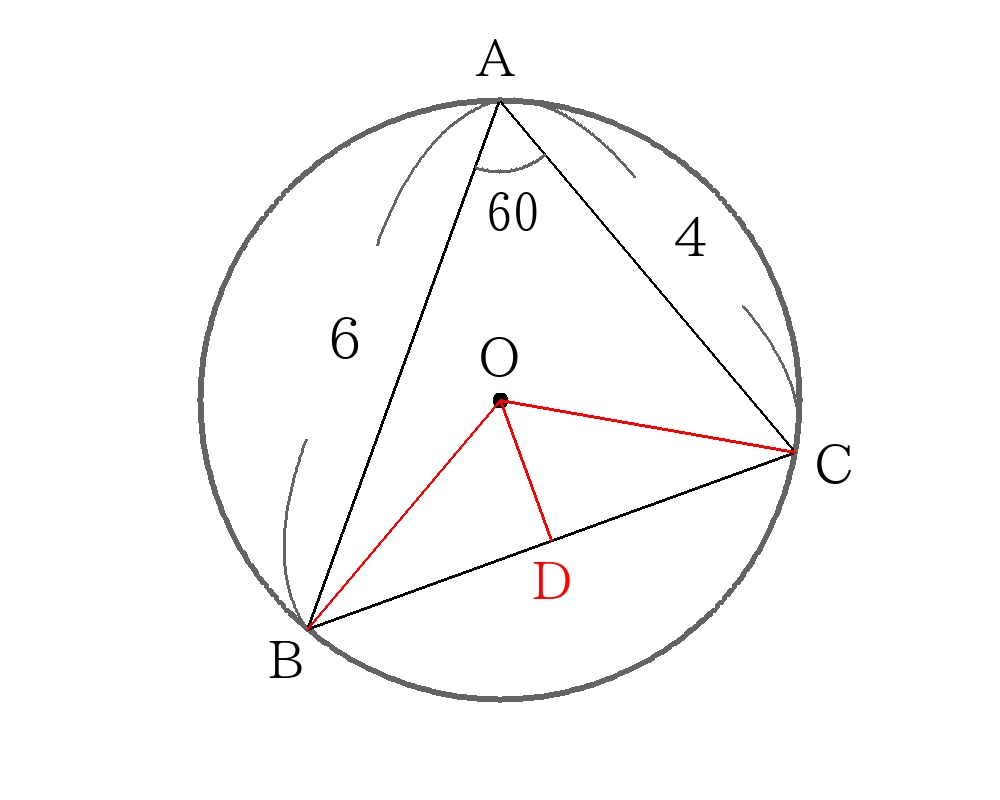
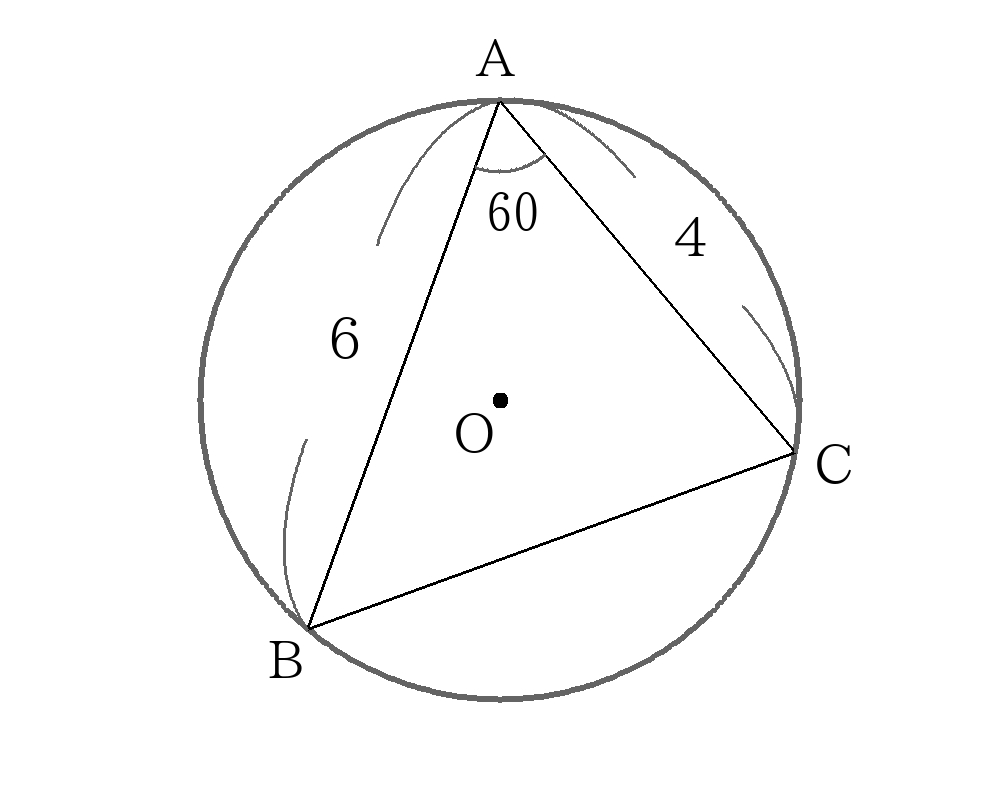
外接円の解き方 中心角から三平方の定理
\(\angle BOC\)は弧\(BC\)に対する中心角であり、円周角\(BAC\)の2倍の大きさなので、
\( \angleBOC=2 \angleBAC=120 \)
\(BC\)に垂線\(OD\)引くと、\(\angle BOD=60\)
内接円を解く段階で\(BC=2 \sqrt{7}\)とわかているので、
\(BD= \dfrac{1}{2}BC= \sqrt{7} \)
また\(\triangle ODB\)は\(1:2:\sqrt{3}\)の直角三角形のため、
\(OB:BD=2: \sqrt{3}=R: \sqrt{7} \)
\(R= \dfrac{2 \sqrt{21}}{3} \)
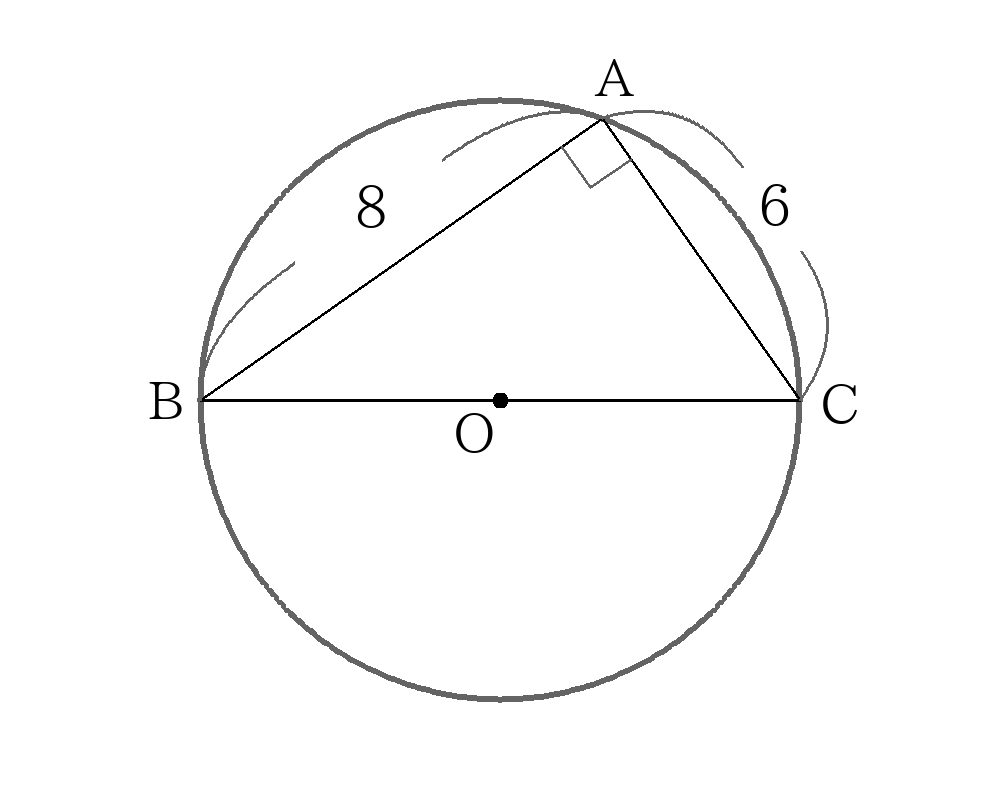
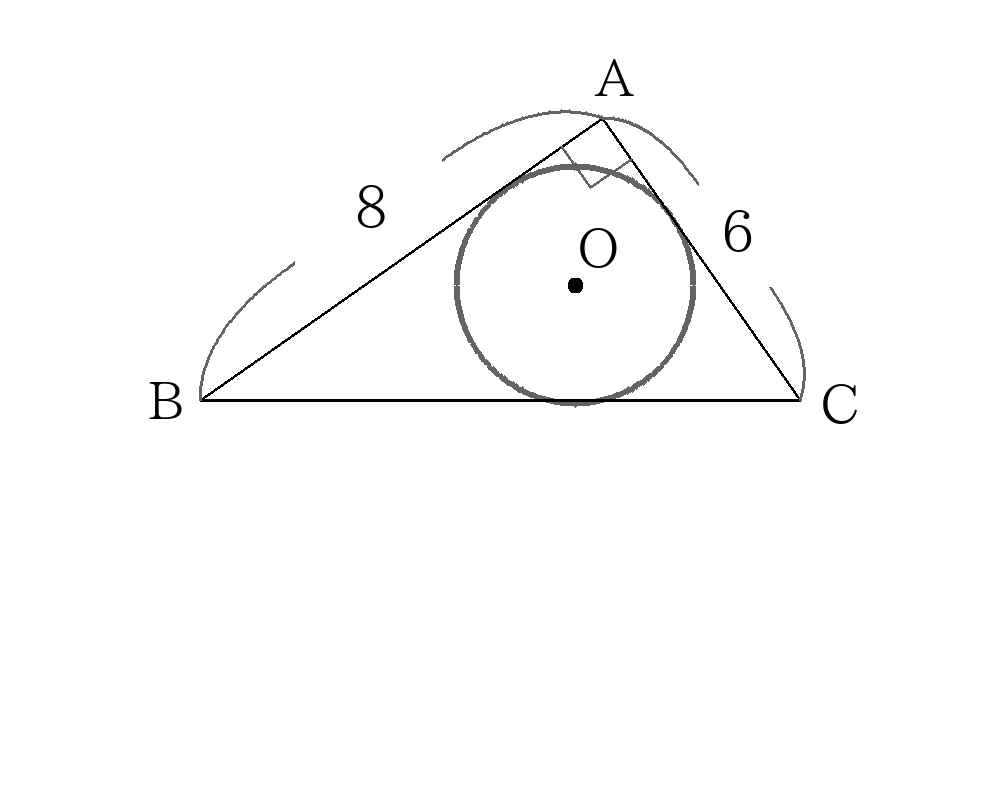
内接円の解き方 面積から求める。
\(\triangle ABC\)において三平方の定理より、
\(BC=10 \)
また、\(\triangle ABC\)の面積を2通りで表すと、
\(S=6 \times 8 \times \dfrac{1}{2}=24 \dots① \)
\(S= \dfrac{1}{2}r(6+8+10)=12r \dots② \)
①、②より
\(r=2 \)
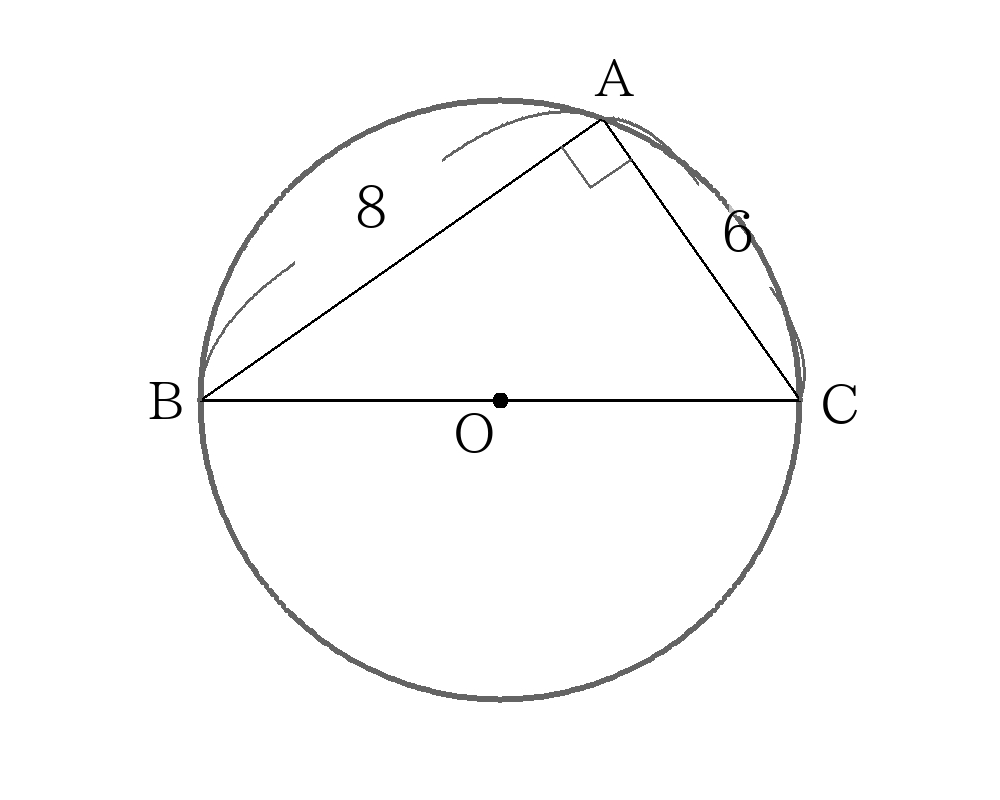
外接円の解き方 三平方の定理
内接円を解く段階で、\(BC=10\)とわかっているので
\(R=OB= \dfrac{1}{2}BC=5 \)
\(R=5 \)
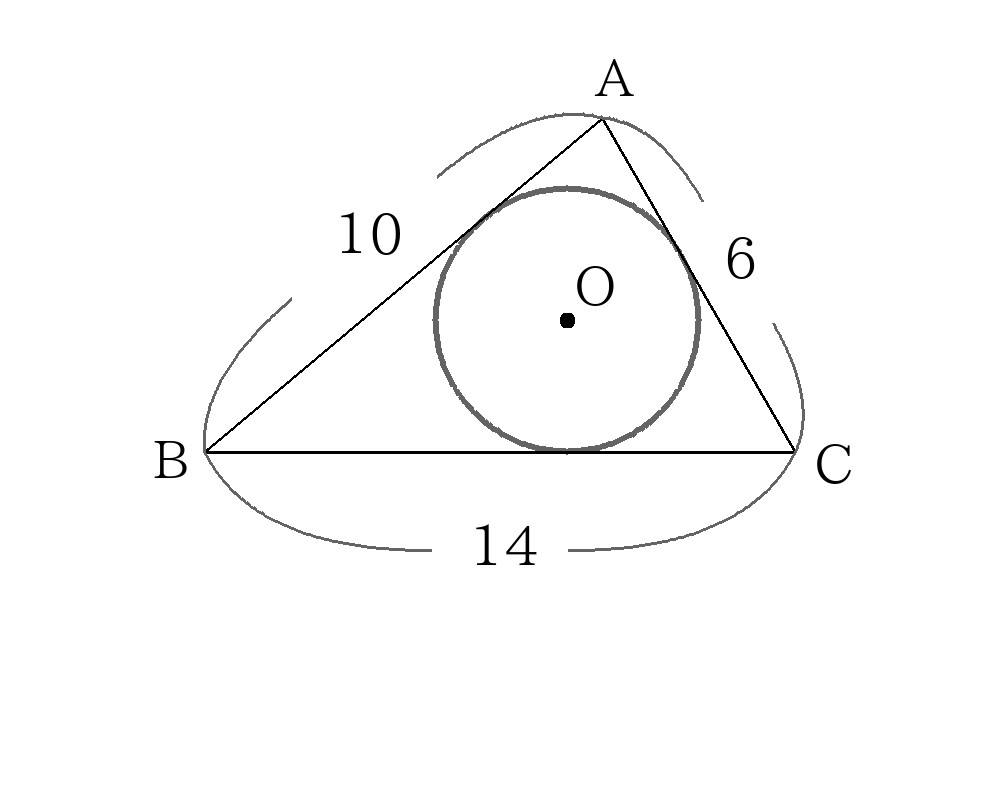
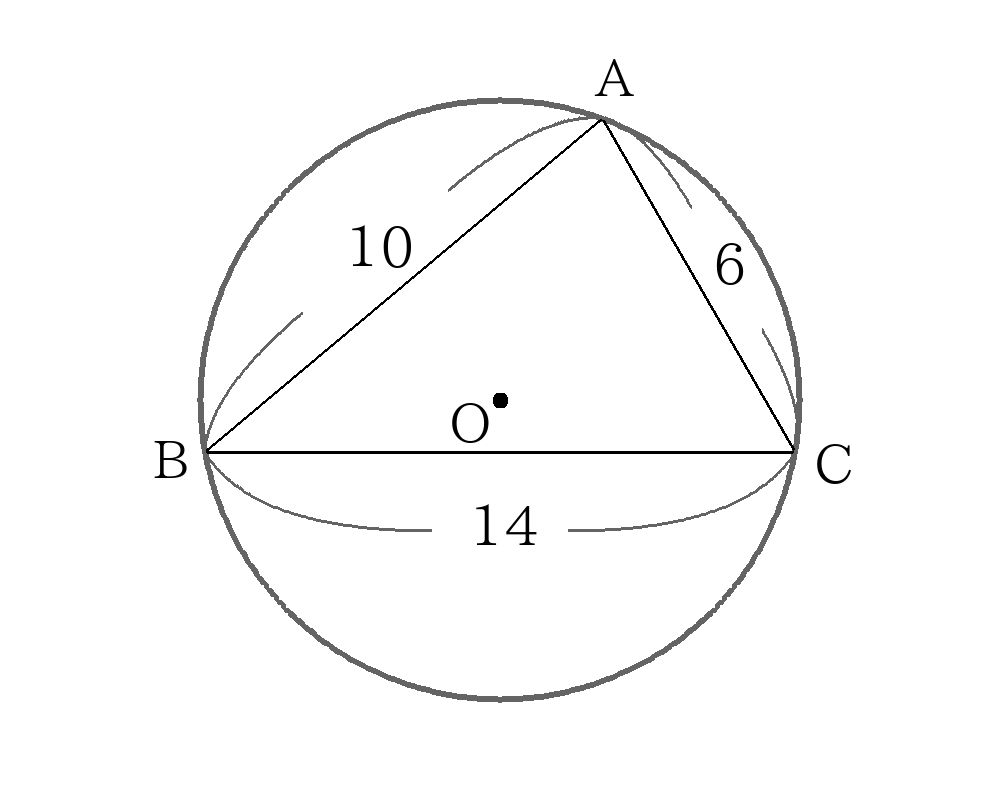
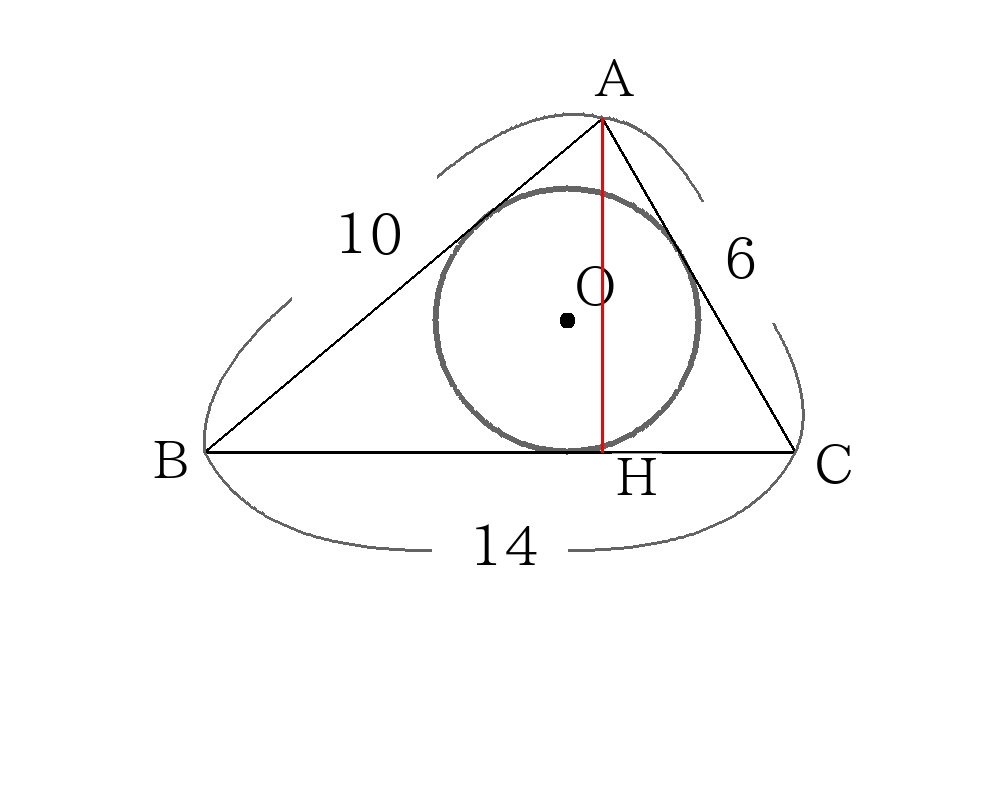
内接円の解き方 面積から逆算
\(ABC\)の面積を計算するために、\(A\)から\(BC\)に垂線\(AH\)をおろす。
\(BH=x\)とすると三平方の定理より
\(AH^2=10^2-x^2=6^2-(14-x)^2 \)
\(x= \dfrac{65}{7} \)
\(AH= \dfrac{15 \sqrt{3}}{7} \)
\( \triangleABC=14 \times \dfrac{15 \sqrt{3}}{7} \times \dfrac{1}{2}=15 \sqrt{3} \)
内接円の半径を\(r\)とすると面積の関係より
\(15 \sqrt{3}= \dfrac{1}{2}(10+6+14)r \)
\(r= \sqrt{3} \)
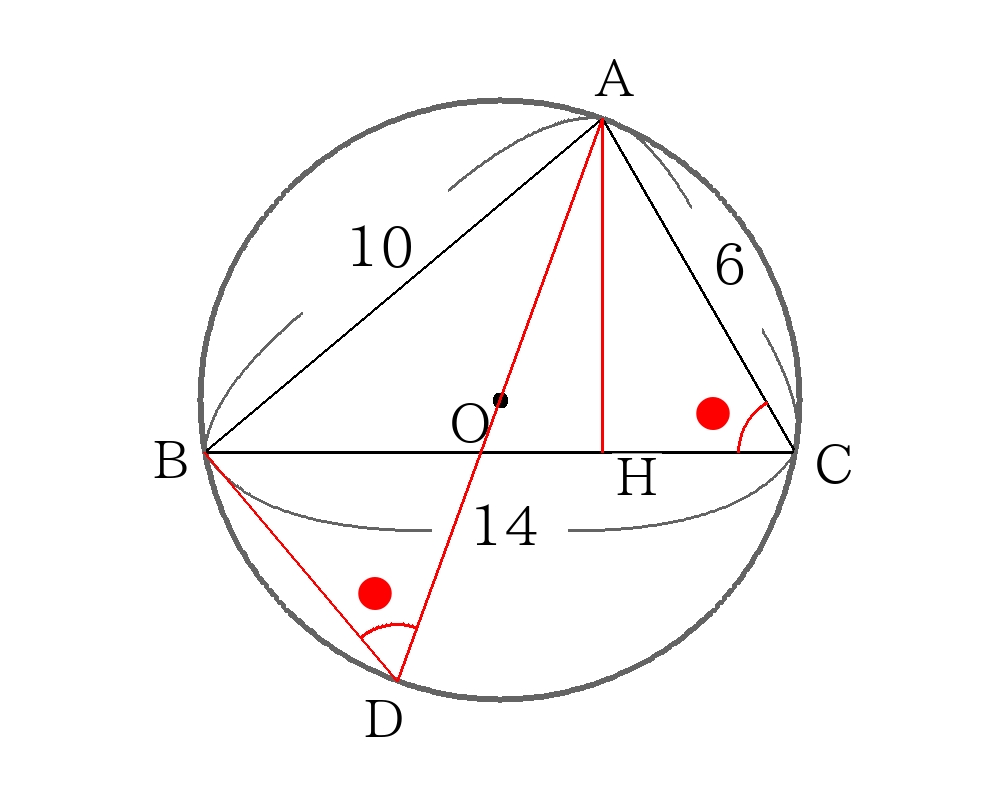
外接円の解き方 直径となる補助線から相似
図のように直径となる補助線\(AD\)を引く。また外接円の半径を\(R\)とする。
\(BAD\)∽\(HAC\)より
\(BA:AD=HA:AC \)
\(10:2R= \dfrac{15 \sqrt{3}}{7}:6 \)
\(R= \dfrac{14}{ \sqrt{3}} \)
\(R= \dfrac{14 \sqrt{3}}{3} \)



コメント